Wave Optics · Physics · JEE Main
MCQ (Single Correct Answer)
In a Young's double slit experiment, the source is white light. One of the slits is covered by red filter and another by a green filter. In this case:
Two plane polarized light waves combine at a certain point whose electric field components are
$$\begin{aligned} & E_1=E_0 \operatorname{Sin} \omega t \\ & E_2=E_0 \operatorname{Sin}\left(\omega t+\frac{\pi}{3}\right) \end{aligned}$$
Find the amplitude of the resultant wave.
Two polarisers $P_1$ and $P_2$ are placed in such a way that the intensity of the transmitted light will be zero. A third polariser $P_3$ is inserted in between $P_1$ and $P_2$, at particular angle between $P_2$ and $P_3$. The transmitted intensity of the light passing the through all three polarisers is maximum. The angle between the polarisers $P_2$ and $P_3$ is :
In a Young's double slit experiment, the slits are separated by 0.2 mm . If the slits separation is increased to 0.4 mm , the percentage change of the fringe width is :
Width of one of the two slits in a Young's double slit interference experiment is half of the other slit. The ratio of the maximum to the minimum intensity in the interference pattern is :
A monochromatic light of frequency $5 \times 10^{14} \mathrm{~Hz}$ travelling through air, is incident on a medium of refractive index ' 2 '. Wavelength of the refracted light will be :
A light wave is propagating with plane wave fronts of the type $x+y+z=$ constant. Th angle made by the direction of wave propagation with the $x$-axis is :
In a Young's double slit experiment, three polarizers are kept as shown in the figure. The transmission axes of $P_1$ and $P_2$ are orthogonal to each other. The polarizer $P_3$ covers both the slits with its transmission axis at $45^{\circ}$ to those of $P_1$ and $P_2$. An unpolarized light of wavelength $\lambda$ and intensity $I_0$ is incident on $P_1$ and $P_2$. The intensity at a point after $P_3$ where the path difference between the light waves from $s_1$ and $s_2$ is $\frac{\lambda}{3}$, is

Young's double slit inteference apparatus is immersed in a liquid of refractive index 1.44. It has slit separation of 1.5 mm . The slits are illuminated by a parallel beam of light whose wavelength in air is 690 nm . The fringe-width on a screen placed behind the plane of slits at a distance of 0.72 m , will be:
The Young's double slit interference experiment is performed using light consisting of 480 nm and 600 nm wavelengths to form interference patterns. The least number of the bright fringes of 480 nm light that are required for the first coincidence with the bright fringes formed by 600 nm light is
The width of one of the two slits in Young's double slit experiment is d while that of the other slit is $x \mathrm{~d}$. If the ratio of the maximum to the minimum intensity in the interference pattern on the screen is $9: 4$ then what is the value of $x$ ? (Assume that the field strength varies according to the slit width.)
A transparent film of refractive index, 2.0 is coated on a glass slab of refractive index, 1.45. What is the minimum thickness of transparent film to be coated for the maximum transmission of Green light of wavelength 550 nm . [Assume that the light is incident nearly perpendicular to the glass surface.]
Given below are two statements. One is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : In Young's double slit experiment, the fringes produced by red light are closer as compared to those produced by blue light.
Reason (R) : The fringe width is directly proportional to the wavelength of light.
In the light of the above statements, choose the correct answer from the options given below :
Given below are two statements : one is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion-(A) : If Young's double slit experiment is performed in an optically denser medium than air, then the consecutive fringes come closer.
Reason-(R) : The speed of light reduces in an optically denser medium than air while its frequency does not change.
In the light of the above statements, choose the most appropriate answer from the options given below :
Given below are two statements :
Statement I : When the white light passed through a prism, the red light bends lesser than yellow and violet.
Statement II : The refractive indices are different for different wavelengths in dispersive medium. In the light of the above statements, chose the correct answer from the options given below :
Light emerges out of a convex lens when a source of light kept at its focus. The shape of wavefront of the light is :
The width of one of the two slits in a Young's double slit experiment is 4 times that of the other slit. The ratio of the maximum of the minimum intensity in the interference pattern is:
When unpolarized light is incident at an angle of $$60^{\circ}$$ on a transparent medium from air, the reflected ray is completely polarized. The angle of refraction in the medium is:
A beam of unpolarised light of intensity $$I_0$$ is passed through a polaroid $$A$$ and then through another polaroid $$B$$ which is oriented so that its principal plane makes an angle of $$45^{\circ}$$ relative to that of $$A$$. The intensity of emergent light is:
The diffraction pattern of a light of wavelength $$400 \mathrm{~nm}$$ diffracting from a slit of width $$0.2 \mathrm{~mm}$$ is focused on the focal plane of a convex lens of focal length $$100 \mathrm{~cm}$$. The width of the $$1^{\text {st }}$$ secondary maxima will be :
In Young's double slit experiment, light from two identical sources are superimposing on a screen. The path difference between the two lights reaching at a point on the screen is $$7 \lambda / 4$$. The ratio of intensity of fringe at this point with respect to the maximum intensity of the fringe is :
When a polaroid sheet is rotated between two crossed polaroids then the transmitted light intensity will be maximum for a rotation of :
In a Young's double slits experiment, the ratio of amplitude of light coming from slits is $$2: 1$$. The ratio of the maximum to minimum intensity in the interference pattern is:
The ratio of intensities at two points $$\mathrm{P}$$ and $$\mathrm{Q}$$ on the screen in a Young's double slit experiment where phase difference between two waves of same amplitude are $$\pi / 3$$ and $$\pi / 2$$, respectively are
The width of fringe is $$2 \mathrm{~mm}$$ on the screen in a double slits experiment for the light of wavelength of $$400 \mathrm{~nm}$$. The width of the fringe for the light of wavelength 600 $$\mathrm{nm}$$ will be:
'$$n$$' polarizing sheets are arranged such that each makes an angle $$45^{\circ}$$ with the preceeding sheet. An unpolarized light of intensity I is incident into this arrangement. The output intensity is found to be $$I / 64$$. The value of $$n$$ will be:
Two polaroide $$\mathrm{A}$$ and $$\mathrm{B}$$ are placed in such a way that the pass-axis of polaroids are perpendicular to each other. Now, another polaroid $$\mathrm{C}$$ is placed between $$\mathrm{A}$$ and $$\mathrm{B}$$ bisecting angle between them. If intensity of unpolarized light is $$\mathrm{I}_{0}$$ then intensity of transmitted light after passing through polaroid $$\mathrm{B}$$ will be:
In a Young's double slit experiment, two slits are illuminated with a light of wavelength $$800 \mathrm{~nm}$$. The line joining $$A_{1} P$$ is perpendicular to $$A_{1} A_{2}$$ as shown in the figure. If the first minimum is detected at $$P$$, the value of slits separation 'a' will be:

The distance of screen from slits D = 5 cm
In Young's double slits experiment, the position of 5$$\mathrm{^{th}}$$ bright fringe from the central maximum is 5 cm. The distance between slits and screen is 1 m and wavelength of used monochromatic light is 600 nm. The separation between the slits is :
Given below are two statements :
Statement I : If the Brewster's angle for the light propagating from air to glass is $$\mathrm{\theta_B}$$, then the Brewster's angle for the light propagating from glass to air is $$\frac{\pi}{2}-\theta_B$$
Statement II : The Brewster's angle for the light propagating from glass to air is $${\tan ^{ - 1}}({\mu _\mathrm{g}})$$ where $$\mathrm{\mu_g}$$ is the refractive index of glass.
In the light of the above statements, choose the correct answer from the options given below :
An unpolarised light beam of intensity $$2 I_{0}$$ is passed through a polaroid P and then through another polaroid Q which is oriented in such a way that its passing axis makes an angle of $$30^{\circ}$$ relative to that of P. The intensity of the emergent light is
Two coherent sources of light interfere. The intensity ratio of two sources is $$1: 4$$. For this interference pattern if the value of $$\frac{I_{\max }+I_{\min }}{I_{\max }-I_{\min }}$$ is equal to $$\frac{2 \alpha+1}{\beta+3}$$, then $$\frac{\alpha}{\beta}$$ will be :
In Young's double slit experiment, the fringe width is $$12 \mathrm{~mm}$$. If the entire arrangement is placed in water of refractive index $$\frac{4}{3}$$, then the fringe width becomes (in mm):
Find the ratio of maximum intensity to the minimum intensity in the interference pattern if the widths of the two slits in Young's experiment are in the ratio of 9 : 16. (Assuming intensity of light is directly proportional to the width of slits)
Using Young's double slit experiment, a monochromatic light of wavelength 5000 $$\mathop A\limits^o $$ produces fringes of fringe width 0.5 mm. If another monochromatic light of wavelength 6000 $$\mathop A\limits^o $$ is used and the separation between the slits is doubled, then the new fringe width will be :
In Young's double slit experiment performed using a monochromatic light of wavelength $$\lambda$$, when a glass plate ($$\mu$$ = 1.5) of thickness x$$\lambda$$ is introduced in the path of the one of the interfering beams, the intensity at the position where the central maximum occurred previously remains unchanged. The value of x will be :
For a specific wavelength 670 nm of light coming from a galaxy moving with velocity v, the observed wavelength is 670.7 nm. The value of v is :
The interference pattern is obtained with two coherent light sources of intensity ratio 4 : 1. And the ratio $${{{I_{\max }} + {I_{\min }}} \over {{I_{\max }} - {I_{\min }}}}$$ is $${5 \over x}$$. Then, the value of x will be equal to :
A light whose electric field vectors are completely removed by using a good polaroid, allowed to incident on the surface of the prism at Brewster's angle. Choose the most suitable option for the phenomenon related to the prism.
The two light beams having intensities I and 9I interfere to produce a fringe pattern on a screen. The phase difference between the beams is $$\pi$$/2 at point P and $$\pi$$ at point Q. Then the difference between the resultant intensities at P and Q will be :
Two light beams of intensities in the ratio of 9 : 4 are allowed to interfere. The ratio of the intensity of maxima and minima will be :
d(t) = d0 + a0 sin$$\omega$$t; where d0, $$\omega$$ and a0 are constants. The difference between the largest fringe width and the smallest fringe width obtained over time is given as :

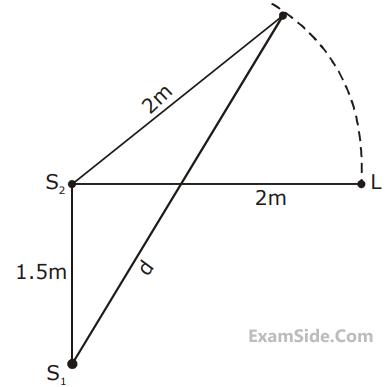
when he is 2 m away from S2. The listener moves away from S1, keeping his distance from S2 fixed. The adjacent maximum of intensity is observed when the listener is at a distance d from S1. Then, d is :
cross-sectional area and uniform intensity
of 3.3 Wm-2 falls normally on a
polariser (cross sectional area 3 $$ \times $$ 10-4 m2) which
rotates about its axis with an angular speed
of 31.4 rad/s. The energy of light passing through
the polariser per revolution, is close to :



What is the angle between the direction of polarization and x-axis ?


A thin air film is formed by putting the convex surface of a plane-convex lens over a plane glass plane. With monochromatic light, this film gives an interference pattern due to light, reflected from the top (convex) surface and the bottom (glass plate) surface of the film.
Statement - $$1$$ : When light reflects from the air-glass plate interface, the reflected wave suffers a phase change of $$\pi .$$
Statement - $$2$$ : The center of the interference pattern is dark.
The initial shape of the wavefront of the beam is
Numerical
In a Young's double slit experiment, two slits are located 1.5 mm apart. The distance of screen from slits is 2 m and the wavelength of the source is 400 nm . If the 20 maxima of the double slit pattern are contained within the central maximum of the single slit diffraction pattern, then the width of each slit is $x \times 10^{-3} \mathrm{~cm}$, where $x$-value is _________ .
If the measured angular separation between the second minimum to the left of the central maximum and the third minimum to the right of the central maximum is $30^{\circ}$ in a single slit diffraction pattern recorded using 628 nm light, then the width of the slit is _______ $\mu$m.
A double slit interference experiment performed with a light of wavelength 600 nm forms an interference fringe pattern on a screen with 10 th bright fringe having its centre at a distance of 10 mm from the central maximum. Distance of the centre of the same 10 th bright fringe from the central maximum when the source of light is replaced by another source of wavelength 660 nm would be ________ mm .
Monochromatic light of wavelength $$500 \mathrm{~nm}$$ is used in Young's double slit experiment. An interference pattern is obtained on a screen. When one of the slits is covered with a very thin glass plate (refractive index $$=1.5$$), the central maximum is shifted to a position previously occupied by the $$4^{\text {th }}$$ bright fringe. The thickness of the glass-plate is __________ $$\mu \mathrm{m}$$.
In a Young's double slit experiment, the intensity at a point is $$\left(\frac{1}{4}\right)^{\text {th }}$$ of the maximum intensity, the minimum distance of the point from the central maximum is _________ $$\mu \mathrm{m}$$. (Given : $$\lambda=600 \mathrm{~nm}, \mathrm{~d}=1.0 \mathrm{~mm}, \mathrm{D}=1.0 \mathrm{~m}$$)
Two slits are $$1 \mathrm{~mm}$$ apart and the screen is located $$1 \mathrm{~m}$$ away from the slits. A light of wavelength $$500 \mathrm{~nm}$$ is used. The width of each slit to obtain 10 maxima of the double slit pattern within the central maximum of the single slit pattern is __________ $$\times 10^{-4} \mathrm{~m}$$.
A parallel beam of monochromatic light of wavelength $$600 \mathrm{~nm}$$ passes through single slit of $$0.4 \mathrm{~mm}$$ width. Angular divergence corresponding to second order minima would be _________ $$\times 10^{-3} \mathrm{~rad}$$.
Two coherent monochromatic light beams of intensities I and $$4 \mathrm{~I}$$ are superimposed. The difference between maximum and minimum possible intensities in the resulting beam is $$x \mathrm{~I}$$. The value of $$x$$ is __________.
In a single slit experiment, a parallel beam of green light of wavelength $$550 \mathrm{~nm}$$ passes through a slit of width $$0.20 \mathrm{~mm}$$. The transmitted light is collected on a screen $$100 \mathrm{~cm}$$ away. The distance of first order minima from the central maximum will be $$x \times 10^{-5} \mathrm{~m}$$. The value of $$x$$ is :
In Young's double slit experiment, carried out with light of wavelength $$5000~\mathop A\limits^o$$, the distance between the slits is $$0.3 \mathrm{~mm}$$ and the screen is at $$200 \mathrm{~cm}$$ from the slits. The central maximum is at $$x=0 \mathrm{~cm}$$. The value of $$x$$ for third maxima is __________ $$\mathrm{mm}$$.
Two wavelengths $$\lambda_1$$ and $$\lambda_2$$ are used in Young's double slit experiment. $$\lambda_1=450 \mathrm{~nm}$$ and $$\lambda_2=650 \mathrm{~nm}$$. The minimum order of fringe produced by $$\lambda_2$$ which overlaps with the fringe produced by $$\lambda_1$$ is $$n$$. The value of $$n$$ is _______.
Two waves of intensity ratio $$1: 9$$ cross each other at a point. The resultant intensities at that point, when (a) Waves are incoherent is $$I_1$$ (b) Waves are coherent is $$I_2$$ and differ in phase by $$60^{\circ}$$. If $$\frac{I_1}{I_2}=\frac{10}{x}$$ then $$x=$$ _________.
In a single slit diffraction pattern, a light of wavelength 6000$$\mathop A\limits^o$$ is used. The distance between the first and third minima in the diffraction pattern is found to be $$3 \mathrm{~mm}$$ when the screen in placed $$50 \mathrm{~cm}$$ away from slits. The width of the slit is _________ $$\times 10^{-4} \mathrm{~m}$$.
In a double slit experiment shown in figure, when light of wavelength $$400 \mathrm{~nm}$$ is used, dark fringe is observed at $$P$$. If $$\mathrm{D}=0.2 \mathrm{~m}$$, the minimum distance between the slits $$S_1$$ and $$S_2$$ is _________ $$\mathrm{mm}$$.

A parallel beam of monochromatic light of wavelength 5000 $$\mathop A\limits^o$$ is incident normally on a single narrow slit of width $$0.001 \mathrm{~mm}$$. The light is focused by convex lens on screen, placed on its focal plane. The first minima will be formed for the angle of diffraction of _________ (degree).
Unpolarised light of intensity 32 Wm$$^{-2}$$ passes through the combination of three polaroids such that the pass axis of the last polaroid is perpendicular to that of the pass axis of first polaroid. If intensity of emerging light is 3 Wm$$^{-2}$$, then the angle between pass axis of first two polaroids is ______________ $$^\circ$$.
A beam of light consisting of two wavelengths $$7000~\mathop A\limits^o $$ and $$5500~\mathop A\limits^o $$ is used to obtain interference pattern in Young's double slit experiment. The distance between the slits is $$2.5 \mathrm{~mm}$$ and the distance between the plane of slits and the screen is $$150 \mathrm{~cm}$$. The least distance from the central fringe, where the bright fringes due to both the wavelengths coincide, is $$n \times 10^{-5} \mathrm{~m}$$. The value of $$n$$ is __________.
As shown in the figure, in Young's double slit experiment, a thin plate of thickness $$t=10 \mu \mathrm{m}$$ and refractive index $$\mu=1.2$$ is inserted infront of slit $$S_{1}$$. The experiment is conducted in air $$(\mu=1)$$ and uses a monochromatic light of wavelength $$\lambda=500 \mathrm{~nm}$$. Due to the insertion of the plate, central maxima is shifted by a distance of $$x \beta_{0} . \beta_{0}$$ is the fringe-width befor the insertion of the plate. The value of the $$x$$ is _____________.

In a Young's double slit experiment, the intensities at two points, for the path differences $\frac{\lambda}{4}$ and $\frac{\lambda}{3}$ ( $\lambda$ being the wavelength of light used) are $I_{1}$ and $I_{2}$ respectively. If $I_{0}$ denotes the intensity produced by each one of the individual slits, then $\frac{I_{1}+I_{2}}{I_{0}}=$ __________.
In Young's double slit experiment, two slits $$S_{1}$$ and $$S_{2}$$ are '$$d$$' distance apart and the separation from slits to screen is $$\mathrm{D}$$ (as shown in figure). Now if two transparent slabs of equal thickness $$0.1 \mathrm{~mm}$$ but refractive index $$1.51$$ and $$1.55$$ are introduced in the path of beam $$(\lambda=4000$$ $$\mathop A\limits^o $$) from $$\mathrm{S}_{1}$$ and $$\mathrm{S}_{2}$$ respectively. The central bright fringe spot will shift by ___________ number of fringes.

Unpolarised light is incident on the boundary between two dielectric media, whose dielectric constants are 2.8 (medium $$-1$$) and 6.8 (medium $$-2$$), respectively. To satisfy the condition, so that the reflected and refracted rays are perpendicular to each other, the angle of incidence should be $${\tan ^{ - 1}}{\left( {1 + {{10} \over \theta }} \right)^{{1 \over 2}}}$$ the value of $$\theta$$ is __________.
(Given for dielectric media, $$\mu_r=1$$)
As shown in the figure, three identical polaroids P$$_1$$, P$$_2$$ and P$$_3$$ are placed one after another. The pass axis of P$$_2$$ and P$$_3$$ are inclined at angle of 60$$^\circ$$ and 90$$^\circ$$ with respect to axis of P$$_1$$. The source S has an intensity of 256 $$\frac{W}{m^2}$$. The intensity of light at point O is ____________ $$\frac{W}{m^2}$$.

Two light beams of intensities 4I and 9I interfere on a screen. The phase difference between these beams on the screen at point A is zero and at point B is $$\pi$$. The difference of resultant intensities, at the point A and B, will be _________ I.
In a Young's double slit experiment, a laser light of 560 nm produces an interference pattern with consecutive bright fringes' separation of 7.2 mm. Now another light is used to produce an interference pattern with consecutive bright fringes' separation of 8.1 mm. The wavelength of second light is __________ nm.
Two beams of light having intensities I and 4I interfere to produce a fringe pattern on a screen. The phase difference between the two beams are $$\pi / 2$$ and $$\pi / 3$$ at points $$\mathrm{A}$$ and $$\mathrm{B}$$ respectively. The difference between the resultant intensities at the two points is $$x I$$. The value of $$x$$ will be ________.
In a double slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the plane of slits. If the screen is moved by 5 $$\times$$ 10$$-$$2 m towards the slits, the change in fringe width is 3 $$\times$$ 10$$-$$3 cm. If the distance between the slits is 1 mm, then the wavelength of the light will be ____________ nm.
In a Young's double slit experiment, an angular width of the fringe is 0.35$$^\circ$$ on a screen placed at 2 m away for particular wavelength of 450 nm. The angular width of the fringe, when whole system is immersed in a medium of refractive index 7/5, is $${1 \over \alpha }$$. The value of $$\alpha$$ is ___________.
In Young's double slit experiment the two slits are 0.6 mm distance apart. Interference pattern is observed on a screen at a distance 80 cm from the slits. The first dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light will be ____________ nm.
Sodium light of wavelengths 650 nm and 655 nm is used to study diffraction at a single slit of aperture 0.5 mm. The distance between the slit and the screen is 2.0 m. The separation between the positions of the first maxima of diffraction pattern obtained in the two cases is ___________ $$\times$$ 10$$-$$5 m.
slit of width 0.6 $$ \times $$ 10–4 m. The maximum possible number of diffraction minima produced on both sides of the central maximum is ___________.