Motion in a Straight Line · Physics · JEE Main
MCQ (Single Correct Answer)
The displacement x versus time graph is shown below.

(A) The average velocity during 0 to 3 s is $10 \mathrm{~m} / \mathrm{s}$
(B) The average velocity during 3 to 5 s is $0 \mathrm{~m} / \mathrm{s}$
(C) The instantaneous velocity at $\mathrm{t}=2 \mathrm{~s}$ is $5 \mathrm{~m} / \mathrm{s}$
(D) The average velocity during 5 to 7 s and instantaneous velocity at $\mathrm{t}=6.5 \mathrm{~s}$ are equal
(E) The average velocity from $t=0$ to $t=9 \mathrm{~s}$ is zero
Choose the correct answer from the options given below :
A particle moves along the $x$-axis and has its displacement $x$ varying with time t according to the equation:
$$ x=\mathrm{c}_0\left(\mathrm{t}^2-2\right)+\mathrm{c}(\mathrm{t}-2)^2 $$
where $\mathrm{c}_0$ and c are constants of appropriate dimensions.
Then, which of the following statements is correct?
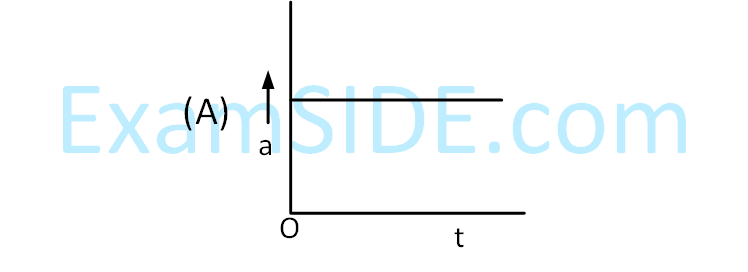
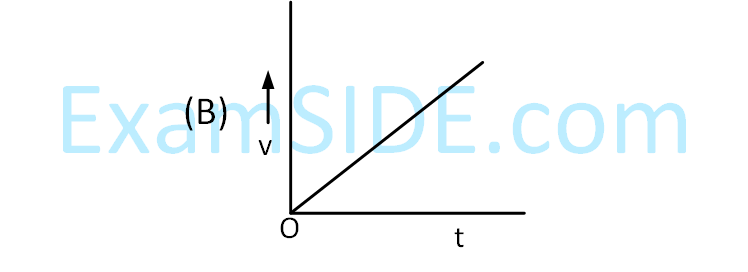
$$ \text {Which of the following curves possibly represent one-dimensional motion of a particle? } $$




Choose the correct answer from the options given below :
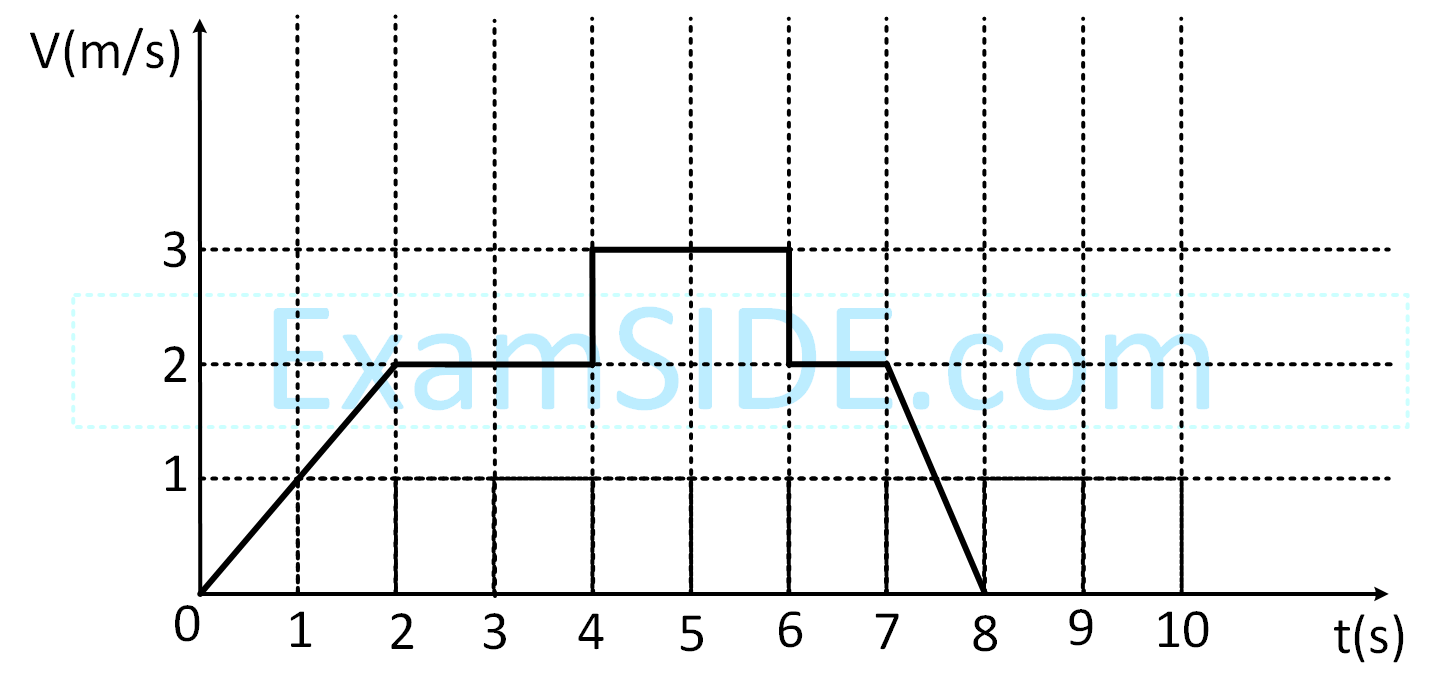
The velocity-time graph of an object moving along a straight line is shown in the figure. What is the distance covered by the object between $t = 0$ to $t = 4s$?

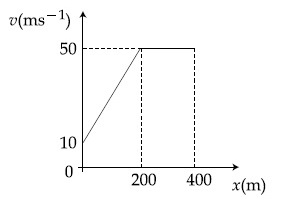
The motion of an airplane is represented by velocity-time graph as shown below. The distance covered by airplane in the first 30.5 second is ̱_______ km .

Two cars are travelling towards each other at speed of $$20 \mathrm{~m} \mathrm{~s}^{-1}$$ each. When the cars are $$300 \mathrm{~m}$$ apart, both the drivers apply brakes and the cars retard at the rate of $$2 \mathrm{~m} \mathrm{~s}^{-2}$$. The distance between them when they come to rest is :
A particle moving in a straight line covers half the distance with speed $$6 \mathrm{~m} / \mathrm{s}$$. The other half is covered in two equal time intervals with speeds $$9 \mathrm{~m} / \mathrm{s}$$ and $$15 \mathrm{~m} / \mathrm{s}$$ respectively. The average speed of the particle during the motion is :
A body projected vertically upwards with a certain speed from the top of a tower reaches the ground in $$t_1$$. If it is projected vertically downwards from the same point with the same speed, it reaches the ground in $$t_2$$. Time required to reach the ground, if it is dropped from the top of the tower, is :
A train starting from rest first accelerates uniformly up to a speed of $$80 \mathrm{~km} / \mathrm{h}$$ for time $$t$$, then it moves with a constant speed for time $$3 t$$. The average speed of the train for this duration of journey will be (in $$\mathrm{km} / \mathrm{h}$$) :
A body travels $$102.5 \mathrm{~m}$$ in $$\mathrm{n}^{\text {th }}$$ second and $$115.0 \mathrm{~m}$$ in $$(\mathrm{n}+2)^{\text {th }}$$ second. The acceleration is :
Train A is moving along two parallel rail tracks towards north with speed $$72 \mathrm{~km} / \mathrm{h}$$ and train B is moving towards south with speed $$108 \mathrm{~km} / \mathrm{h}$$. Velocity of train B with respect to A and velocity of ground with respect to B are (in $$\mathrm{ms}^{-1}$$):
The relation between time '$$t$$' and distance '$$x$$' is $$t=\alpha x^2+\beta x$$, where $$\alpha$$ and $$\beta$$ are constants. The relation between acceleration $$(a)$$ and velocity $$(v)$$ is :
A particle is moving in a straight line. The variation of position '$$x$$' as a function of time '$$t$$' is given as $$x=\left(t^3-6 t^2+20 t+15\right) m$$. The velocity of the body when its acceleration becomes zero is :
A body starts moving from rest with constant acceleration covers displacement $$S_1$$ in first $$(p-1)$$ seconds and $$\mathrm{S}_2$$ in first $$p$$ seconds. The displacement $$\mathrm{S}_1+\mathrm{S}_2$$ will be made in time :
The distance travelled by an object in time $$t$$ is given by $$s=(2.5) t^{2}$$. The instantaneous speed of the object at $$\mathrm{t}=5 \mathrm{~s}$$ will be:
A passenger sitting in a train A moving at $$90 \mathrm{~km} / \mathrm{h}$$ observes another train $$\mathrm{B}$$ moving in the opposite direction for $$8 \mathrm{~s}$$. If the velocity of the train B is $$54 \mathrm{~km} / \mathrm{h}$$, then length of train B is:
Two trains 'A' and 'B' of length '$$l$$' and '$$4 l$$' are travelling into a tunnel of length '$$\mathrm{L}$$' in parallel tracks from opposite directions with velocities $$108 \mathrm{~km} / \mathrm{h}$$ and $$72 \mathrm{~km} / \mathrm{h}$$, respectively. If train 'A' takes $$35 \mathrm{~s}$$ less time than train 'B' to cross the tunnel then. length '$$L$$' of tunnel is :
(Given $$\mathrm{L}=60 l$$ )
A ball is thrown vertically upward with an initial velocity of $$150 \mathrm{~m} / \mathrm{s}$$. The ratio of velocity after $$3 \mathrm{~s}$$ and $$5 \mathrm{~s}$$ is $$\frac{x+1}{x}$$. The value of $$x$$ is ___________.
$$\left\{\right.$$ take, $$\left.g=10 \mathrm{~m} / \mathrm{s}^{2}\right\}$$
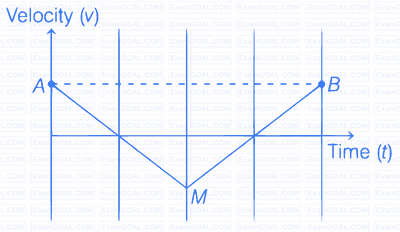
From the $$\mathrm{v}-t$$ graph shown, the ratio of distance to displacement in $$25 \mathrm{~s}$$ of motion is:

A person travels $$x$$ distance with velocity $$v_{1}$$ and then $$x$$ distance with velocity $$v_{2}$$ in the same direction. The average velocity of the person is $$\mathrm{v}$$, then the relation between $$v, v_{1}$$ and $$v_{2}$$ will be.
The position-time graphs for two students A and B returning from the school to their homes are shown in figure.

(A) A lives closer to the school
(B) B lives closer to the school
(C) A takes lesser time to reach home
(D) A travels faster than B
(E) B travels faster than A
Choose the correct answer from the options given below :
Given below are two statements
Statement I : Area under velocity- time graph gives the distance travelled by the body in a given time.
Statement II : Area under acceleration- time graph is equal to the change in velocity- in the given time.
In the light of given statements, choose the correct answer from the options given below.
A particle starts with an initial velocity of $$10.0 \mathrm{~ms}^{-1}$$ along $$x$$-direction and accelerates uniformly at the rate of $$2.0 \mathrm{~ms}^{-2}$$. The time taken by the particle to reach the velocity of $$60.0 \mathrm{~ms}^{-1}$$ is __________.
An object moves with speed $$v_1,v_2$$ and $$v_3$$ along a line segment AB, BC and CD respectively as shown in figure. Where AB = BC and AD = 3AB, then average speed of the object will be:

Match Column-I with Column-II :
| Column-I ($$x$$-t graphs) |
Column-II ($$v$$-t graphs) |
||
|---|---|---|---|
| A. |  |
I. |  |
| B. |  |
II. |  |
| C. |  |
III. |  |
| D. |  |
IV. |  |
Choose the correct answer from the options given below:
The distance travelled by a particle is related to time t as $$x=4\mathrm{t}^2$$. The velocity of the particle at t=5s is :-
A car travels a distance of '$$x$$' with speed $$v_1$$ and then same distance '$$x$$' with speed $$v_2$$ in the same direction. The average speed of the car is :
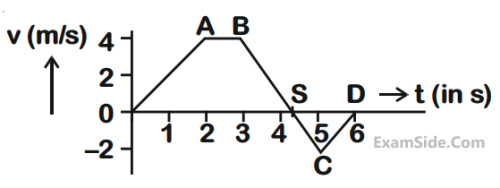
The velocity time graph of a body moving in a straight line is shown in the figure.

The ratio of displacement to distance travelled by the body in time 0 to 10s is :
A juggler throws balls vertically upwards with same initial velocity in air. When the first ball reaches its highest position, he throws the next ball. Assuming the juggler throws n balls per second, the maximum height the balls can reach is
A ball is released from a height h. If $$t_{1}$$ and $$t_{2}$$ be the time required to complete first half and second half of the distance respectively. Then, choose the correct relation between $$t_{1}$$ and $$t_{2}$$.
A ball is thrown up vertically with a certain velocity so that, it reaches a maximum height h. Find the ratio of the times in which it is at height $$\frac{h}{3}$$ while going up and coming down respectively.
If $$\mathrm{t}=\sqrt{x}+4$$, then $$\left(\frac{\mathrm{d} x}{\mathrm{~d} t}\right)_{\mathrm{t}=4}$$ is :
A NCC parade is going at a uniform speed of $$9 \mathrm{~km} / \mathrm{h}$$ under a mango tree on which a monkey is sitting at a height of $$19.6 \mathrm{~m}$$. At any particular instant, the monkey drops a mango. A cadet will receive the mango whose distance from the tree at time of drop is: (Given $$g=9.8 \mathrm{~m} / \mathrm{s}^{2}$$ )
The velocity of the bullet becomes one third after it penetrates 4 cm in a wooden block. Assuming that bullet is facing a constant resistance during its motion in the block. The bullet stops completely after travelling at (4 + x) cm inside the block. The value of x is :
A bullet is shot vertically downwards with an initial velocity of $$100 \mathrm{~m} / \mathrm{s}$$ from a certain height. Within 10 s, the bullet reaches the ground and instantaneously comes to rest due to the perfectly inelastic collision. The velocity-time curve for total time $$\mathrm{t}=20 \mathrm{~s}$$ will be:
(Take g = 10 m/s2).
A small toy starts moving from the position of rest under a constant acceleration. If it travels a distance of 10m in t s, the distance travelled by the toy in the next t s will be :
Two balls A and B are placed at the top of 180 m tall tower. Ball A is released from the top at t = 0 s. Ball B is thrown vertically down with an initial velocity 'u' at t = 2 s. After a certain time, both balls meet 100 m above the ground. Find the value of 'u' in ms$$-$$1. [use g = 10 ms$$-$$2] :
Two buses P and Q start from a point at the same time and move in a straight line and their positions are represented by $${X_P}(t) = \alpha t + \beta {t^2}$$ and $${X_Q}(t) = ft - {t^2}$$. At what time, both the buses have same velocity?
(takes the value of g as 10 m/s2)
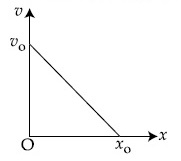
The acceleration $$-$$ displacement graph of the same particle is represented by :
The acceleration-displacement graph of the bicycle's motion is best described by :
[g is the acceleration due to gravity]
(graph are drawn schematically and on not to scale)
(take the distance between the tracks as negligible)
x(t) = at + bt2 – ct3
where a, b and c are constants. When the particle attains zero acceleration, then its velocity will be :
What is the magnitude of the acceleration at t = 1 ?
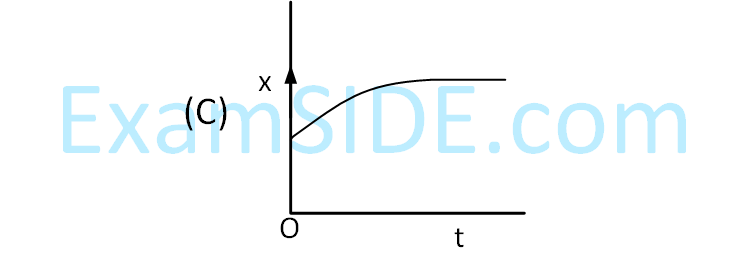
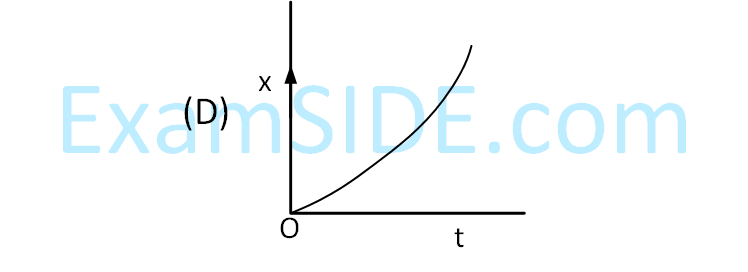

(Assume stones do not rebound after hitting the ground and neglect air resistance, take $$g = 10m/{s^2}$$)
(The figures are schematic and not drawn to scale)
$${{dv} \over {dt}} = - 2.5\sqrt v $$ where v is the instantaneous speed. The time taken by the object, to come to rest, would be :
Then the velocity as a function of time and the height as a function of time will be :
Numerical
A person travelling on a straight line moves with a uniform velocity $v_1$ for a distance $x$ and with a uniform velocity $v_2$ for the next $\frac{3}{2} x$ distance. The average velocity in this motion is $\frac{50}{7} \mathrm{~m} / \mathrm{s}$. If $v_1$ is $5 \mathrm{~m} / \mathrm{s}$ then $v_2=$ __________ $\mathrm{m} / \mathrm{s}$.
Two cars P and Q are moving on a road in the same direction. Acceleration of car P increases linearly with time whereas car Q moves with a constant acceleration. Both cars cross each other at time t = 0, for the first time. The maximum possible number of crossing(s) (including the crossing at t = 0) is ________.
A particle moves in a straight line so that its displacement $$x$$ at any time $$t$$ is given by $$x^2=1+t^2$$. Its acceleration at any time $$\mathrm{t}$$ is $$x^{-\mathrm{n}}$$ where $$\mathrm{n}=$$ _________.
A body moves on a frictionless plane starting from rest. If $$\mathrm{S_n}$$ is distance moved between $$\mathrm{t=n-1}$$ and $$\mathrm{t}=\mathrm{n}$$ and $$\mathrm{S}_{\mathrm{n}-1}$$ is distance moved between $$\mathrm{t}=\mathrm{n}-2$$ and $$\mathrm{t}=\mathrm{n}-1$$, then the ratio $$\frac{\mathrm{S}_{\mathrm{n}-1}}{\mathrm{~S}_{\mathrm{n}}}$$ is $$\left(1-\frac{2}{x}\right)$$ for $$\mathrm{n}=10$$. The value of $$x$$ is __________.
A bus moving along a straight highway with speed of $$72 \mathrm{~km} / \mathrm{h}$$ is brought to halt within $$4 s$$ after applying the brakes. The distance travelled by the bus during this time (Assume the retardation is uniform) is ________ $$m$$.
The velocity of the particle when its acceleration becomes zero is _________ $\mathrm{m} / \mathrm{s}$.
The displacement and the increase in the velocity of a moving particle in the time interval of $$t$$ to $$(t+1) \mathrm{s}$$ are $$125 \mathrm{~m}$$ and $$50 \mathrm{~m} / \mathrm{s}$$, respectively. The distance travelled by the particle in $$(\mathrm{t}+2)^{\mathrm{th}} \mathrm{s}$$ is _________ m.
A body falling under gravity covers two points $$A$$ and $$B$$ separated by $$80 \mathrm{~m}$$ in $$2 \mathrm{~s}$$. The distance of upper point A from the starting point is _________ $$\mathrm{m}$$ (use $$\mathrm{g}=10 \mathrm{~ms}^{-2}$$).
For a train engine moving with speed of $$20 \mathrm{~ms}^{-1}$$, the driver must apply brakes at a distance of 500 $$\mathrm{m}$$ before the station for the train to come to rest at the station. If the brakes were applied at half of this distance, the train engine would cross the station with speed $$\sqrt{x} \mathrm{~ms}^{-1}$$. The value of $$x$$ is ____________.
(Assuming same retardation is produced by brakes)
A horse rider covers half the distance with $$5 \mathrm{~m} / \mathrm{s}$$ speed. The remaining part of the distance was travelled with speed $$10 \mathrm{~m} / \mathrm{s}$$ for half the time and with speed $$15 \mathrm{~m} / \mathrm{s}$$ for other half of the time. The mean speed of the rider averaged over the whole time of motion is $$\frac{x}{7} \mathrm{~m} / \mathrm{s}$$. The value of $$x$$ is ___________.
A tennis ball is dropped on to the floor from a height of 9.8 m. It rebounds to a height 5.0 m. Ball comes in contact with the floor for 0.2s. The average acceleration during contact is ___________ ms$$^{-2}$$.
(Given g = 10 ms$$^{-2}$$)
A ball is thrown vertically upwards with a velocity of $$19.6 \mathrm{~ms}^{-1}$$ from the top of a tower. The ball strikes the ground after $$6 \mathrm{~s}$$. The height from the ground up to which the ball can rise will be $$\left(\frac{k}{5}\right) \mathrm{m}$$. The value of $$\mathrm{k}$$ is __________. (use $$\mathrm{g}=9.8 \mathrm{~m} / \mathrm{s}^{2}$$)
A particle is moving in a straight line such that its velocity is increasing at 5 ms$$-$$1 per meter. The acceleration of the particle is _____________ ms$$-$$2 at a point where its velocity is 20 ms$$-$$1.
A car is moving with speed of $$150 \mathrm{~km} / \mathrm{h}$$ and after applying the break it will move $$27 \mathrm{~m}$$ before it stops. If the same car is moving with a speed of one third the reported speed then it will stop after travelling ___________ m distance.
A car covers AB distance with first one-third at velocity v1 ms$$-$$1, second one-third at v2 ms$$-$$1 and last one-third at v3 ms$$-$$1. If v3 = 3v1, v2 = 2v1 and v1 = 11 ms$$-$$1 then the average velocity of the car is _____________ ms$$-$$1.

A ball is projected vertically upward with an initial velocity of 50 ms$$-$$1 at t = 0s. At t = 2s, another ball is projected vertically upward with same velocity. At t = __________ s, second ball will meet the first ball (g = 10 ms$$-$$2).
A ball of mass 0.5 kg is dropped from the height of 10 m. The height, at which the magnitude of velocity becomes equal to the magnitude of acceleration due to gravity, is ________ m. [Use g = 10 m/s2]
From the top of a tower, a ball is thrown vertically upward which reaches the ground in 6 s. A second ball thrown vertically downward from the same position with the same speed reaches the ground in 1.5 s. A third ball released, from the rest from the same location, will reach the ground in ____________ s.
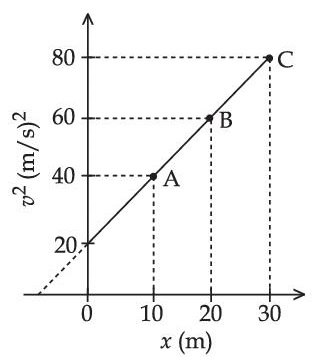

x2 = at2 + 2bt + c. If the acceleration of the particle depends on x as x–n, where n is an integer, the value of n is __________