Rotational Motion · Physics · JEE Main
MCQ (Single Correct Answer)
A rod of linear mass density 'λ' and length 'L' is bent to form a ring of radius 'R'. Moment of inertia of ring about any of its diameter is.
Which of the following are correct expression for torque acting on a body?
A. $\vec{\tau}=\vec{r} \times \vec{L}$
B. $\vec{\tau}=\frac{d}{d t}(\vec{r} \times \vec{p})$
C. $\vec{\tau}=\vec{r} \times \frac{d \vec{p}}{d t}$
D. $\vec{\tau}=I \vec{\alpha}$
E. $\vec{\tau}=\vec{r} \times \vec{F}$
( $\vec{r}=$ position vector; $\vec{p}=$ linear momentum; $\vec{L}=$ angular momentum; $\vec{\alpha}=$ angular acceleration; $I=$ moment of inertia; $\vec{F}=$ force; $t=$ time)
Choose the correct answer from the options given below:
If $\vec{L}$ and $\vec{P}$ represent the angular momentum and linear momentum respectively of a particle of mass ' $m$ ' having position vector as $\vec{r}=a(\hat{i} \cos \omega t+\hat{j} \sin \omega t)$. The direction of force is
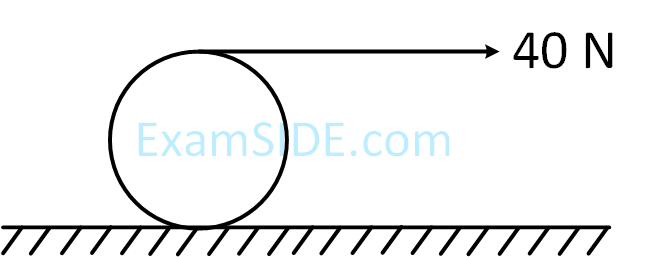
A force of 49 N acts tangentially at the highest point of a sphere (solid) of mass 20 kg , kept on a rough horizontal plane. If the sphere rolls without slipping, then the acceleration of the center of the sphere is

Moment of inertia of a rod of mass ' M ' and length ' L ' about an axis passing through its center and normal to its length is ' $\alpha$ '. Now the rod is cut into two equal parts and these parts are joined symmetrically to form a cross shape. Moment of inertia of cross about an axis passing through its center and normal to plane containing cross is :
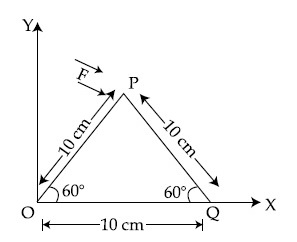
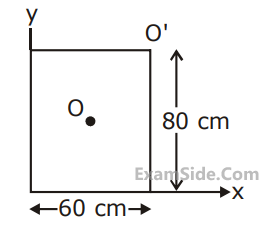
A square Lamina OABC of length 10 cm is pivoted at ' $\mathrm{O}^{\prime}$. Forces act at Lamina as shown in figure. If Lamina remains stationary, then the magnitude of F is :

A cord of negligible mass is wound around the rim of a wheel supported by spokes with negligible mass. The mass of wheel is 10 kg and radius is 10 cm and it can freely rotate without any friction. Initially the wheel is at rest. If a steady pull of 20 N is applied on the cord, the angular velocity of the wheel, after the cord is unwound by 1 m , would be:

A uniform rod of mass 250 g having length 100 cm is balanced on a sharp edge at 40 cm mark. A mass of 400 g is suspended at 10 cm mark. To maintain the balance of the rod, the mass to be suspended at 90 cm mark, is
A solid sphere and a hollow sphere of the same mass and of same radius are rolled on an inclined plane. Let the time taken to reach the bottom by the solid sphere and the hollow sphere be $t_1$ and $t_2$, respectively, then
A solid sphere is rolling without slipping on a horizontal plane. The ratio of the linear kinetic energy of the centre of mass of the sphere and rotational kinetic energy is :
A uniform solid cylinder of mass ' m ' and radius ' r ' rolls along an inclined rough plane of inclination $45^{\circ}$. If it starts to roll from rest from the top of the plane then the linear acceleration of the cylinder's axis will be
A circular disk of radius R meter and mass M kg is rotating around the axis perpendicular to the disk. An external torque is applied to the disk such that $\theta(t)=5 t^2-8 t$, where $\theta(t)$ is the angular position of the rotating disc as a function of time $t$. How much power is delivered by the applied torque, when $t=2 \mathrm{~s}$ ?
A solid sphere of mass ' $m$ ' and radius ' $r$ ' is allowed to roll without slipping from the highest point of an inclined plane of length ' $L$ ' and makes an angle $30^{\circ}$ with the horizontal. The speed of the particle at the bottom of the plane is $v_1$. If the angle of inclination is increased to $45^{\circ}$ while keeping $L$ constant. Then the new speed of the sphere at the bottom of the plane is $v_2$. The ratio $v_1^2: v_2^2$ is
The torque due to the force $(2 \hat{i}+\hat{j}+2 \hat{k})$ about the origin, acting on a particle whose position vector is $(\hat{i}+\hat{j}+\hat{k})$, would be
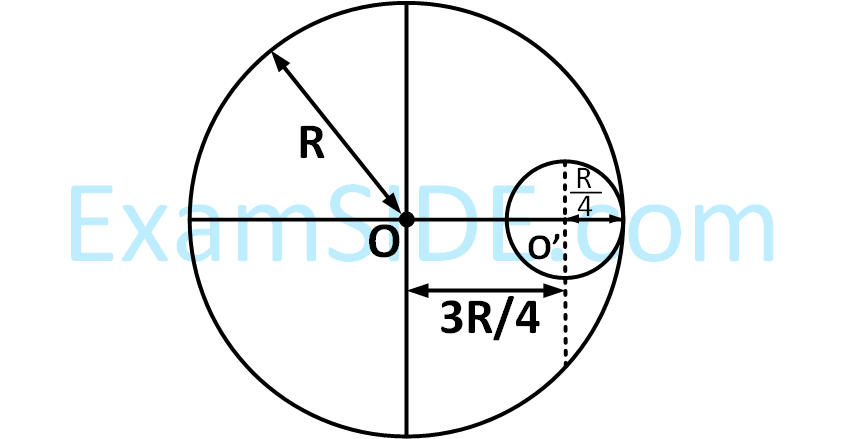
A uniform circular disc of radius ' $\mathrm{R}^{\prime}$ and mass ' $\mathrm{M}^{\prime}$ is rotating about an axis perpendicular to its plane and passing through its centre. A small circular part of radius $R / 2$ is removed from the original disc as shown in the figure. Find the moment of inertia of the remaining part of the original disc about the axis as given above.

A thin circular disc of mass $$\mathrm{M}$$ and radius $$\mathrm{R}$$ is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with angular velocity $$\omega$$. If another disc of same dimensions but of mass $$\mathrm{M} / 2$$ is placed gently on the first disc co-axially, then the new angular velocity of the system is :
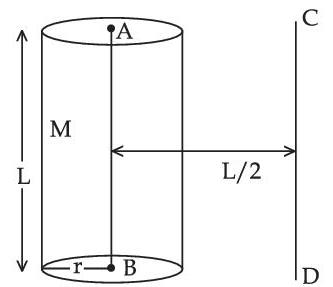
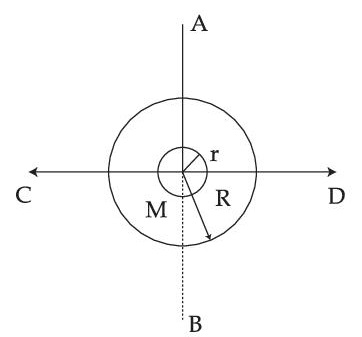
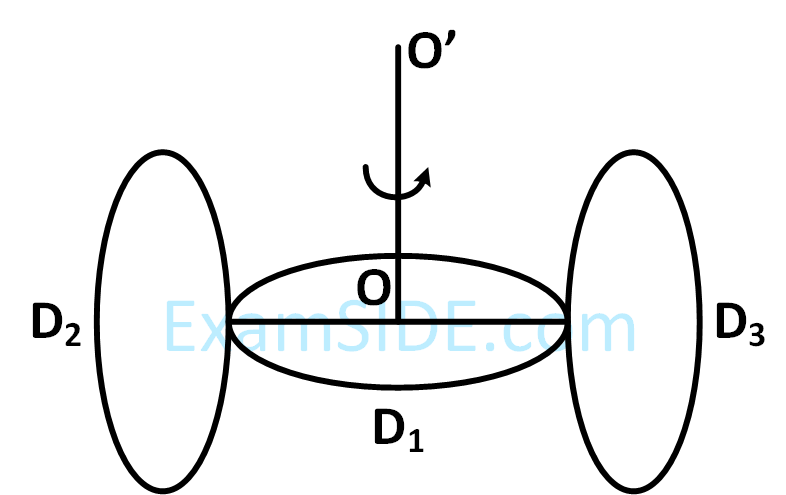
Ratio of radius of gyration of a hollow sphere to that of a solid cylinder of equal mass, for moment of Inertia about their diameter axis $$A B$$ as shown in figure is $$\sqrt{8 / x}$$. The value of $$x$$ is :


A particle of mass $$\mathrm{m}$$ is projected with a velocity '$$\mathrm{u}$$' making an angle of $$30^{\circ}$$ with the horizontal. The magnitude of angular momentum of the projectile about the point of projection when the particle is at its maximum height $$\mathrm{h}$$ is :
A heavy iron bar of weight $$12 \mathrm{~kg}$$ is having its one end on the ground and the other on the shoulder of a man. The rod makes an angle $$60^{\circ}$$ with the horizontal, the weight experienced by the man is :
A disc is rolling without slipping on a surface. The radius of the disc is $$R$$. At $$t=0$$, the top most point on the disc is $$\mathrm{A}$$ as shown in figure. When the disc completes half of its rotation, the displacement of point A from its initial position is

Given below are two statements: one is labelled as Assertion $$\mathbf{A}$$ and the other is labelled as Reason $$\mathbf{R}$$
Assertion A : An electric fan continues to rotate for some time after the current is switched off.
Reason R : Fan continues to rotate due to inertia of motion.
In the light of above statements, choose the most appropriate answer from the options given below.
An object of mass 8 kg is hanging from one end of a uniform rod CD of mass 2 kg and length 1 m pivoted at its end C on a vertical wall as shown in figure. It is supported by a cable AB such that the system is in equilibrium. The tension in the cable is (Take g = 10 m/s$$^2$$)

The torque of a force $$5 \hat{i}+3 \hat{j}-7 \hat{k}$$ about the origin is $$\tau$$. If the force acts on a particle whose position vector is $$2 i+2 j+k$$, then the value of $$\tau$$ will be
A solid cylinder and a solid sphere, having same mass $$M$$ and radius $$R$$, roll down the same inclined plane from top without slipping. They start from rest. The ratio of velocity of the solid cylinder to that of the solid sphere, with which they reach the ground, will be :
A spherical shell of 1 kg mass and radius R is rolling with angular speed $$\omega$$ on horizontal plane (as shown in figure). The magnitude of angular momentum of the shell about the origin O is $${a \over 3}$$ R2$$\omega$$. The value of a will be :

A ball is spun with angular acceleration $$\alpha$$ = 6t2 $$-$$ 2t where t is in second and $$\alpha$$ is in rads$$-$$2. At t = 0, the ball has angular velocity of 10 rads$$-$$1 and angular position of 4 rad. The most appropriate expression for the angular position of the ball is :
A $$\sqrt {34} $$ m long ladder weighing 10 kg leans on a frictionless wall. Its feet rest on the floor 3 m away from the wall as shown in the figure. If Ef and Fw are the reaction forces of the floor and the wall, then ratio of $${F_w}/{F_f}$$ will be :
(Use g = 10 m/s2.)

Match List-I with List-II
| List-I | List-II | ||
|---|---|---|---|
| (A) | Moment of inertia of solid sphere of radius R about any tangent. | (I) | $${5 \over 3}M{R^2}$$ |
| (B) | Moment of inertia of hollow sphere of radius (R) about any tangent. | (II) | $${7 \over 5}M{R^2}$$ |
| (C) | Moment of inertia of circular ring of radius (R) about its diameter. | (III) | $${1 \over 4}M{R^2}$$ |
| (D) | Moment of inertia of circular disc of radius (R) about any diameter. | (IV) | $${1 \over 2}M{R^2}$$ |
Choose the correct answer from the options given below :
One end of a massless spring of spring constant k and natural length l0 is fixed while the other end is connected to a small object of mass m lying on a frictionless table. The spring remains horizontal on the table. If the object is made to rotate at an angular velocity $$\omega$$ about an axis passing through fixed end, then the elongation of the spring will be :
A solid spherical ball is rolling on a frictionless horizontal plane surface about its axis of symmetry. The ratio of rotational kinetic energy of the ball to its total kinetic energy is
A thin circular ring of mass M and radius R is rotating with a constant angular velocity 2 rads$$-$$1 in a horizontal plane about an axis vertical to its plane and passing through the center of the ring. If two objects each of mass m be attached gently to the opposite ends of a diameter of ring, the ring will then rotate with an angular velocity (in rads$$-$$1).
If force $$\overrightarrow F = 3\widehat i + 4\widehat j - 2\widehat k$$ acts on a particle position vector $$2\widehat i + \widehat j + 2\widehat k$$ then, the torque about the origin will be :
| List-I | List-II |
|---|---|
| (a) MI of the rod (length L, Mass M, about an axis $$ \bot $$ to the rod passing through the midpoint) | (i) $$8M{L^2}/3$$ |
| (b) MI of the rod (length L, Mass 2M, about an axis $$ \bot $$ to the rod passing through one of its end) | (ii) $$M{L^2}/3$$ |
| (c) MI of the rod (length 2L, Mass M, about an axis $$ \bot $$ to the rod passing through its midpoint) | (iii) $$M{L^2}/12$$ |
| (d) MI of the rod (Length 2L, Mass 2M, about an axis $$ \bot $$ to the rod passing through one of its end) | (iv) $$2M{L^2}/3$$ |
Choose the correct answer from the options given below:
Assertion A : Moment of inertia of a circular disc of mass 'M' and radius 'R' about X, Y axes (passing through its plane) and Z-axis which is perpendicular to its plane were found to be Ix, Iy and Iz respectively. The respectively radii of gyration about all the three axes will be the same.
Reason R : A rigid body making rotational motion has fixed mass and shape. In the light of the above statements, choose the most appropriate answer from the options given below :
The correct statement for this situation is
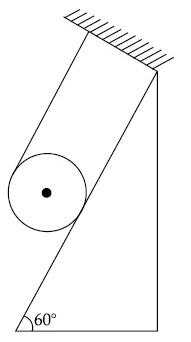
[The coefficient of static friction, $$\mu$$s' is 0.4]
I1 = M.I. of thin circular ring about its diameter,
I2 = M.I. of circular disc about an axis perpendicular to disc and going through the centre,
I3 = M.I. of solid cylinder about its axis and
I4 = M.I. of solid sphere about its diameter.
Then :
$$\lambda \left( x \right) = {\lambda _0}\left( {1 + {x \over L}} \right)$$, where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicular to the rod is :
(i) in its plane with a time period T1 and,
(ii) back and forth in a direction perpendicular to its plane,
with a period T2. The ratio $${{{T_1}} \over {{T_2}}}$$ will be :
R2 = $$\alpha $$R made of the same material. If the ratio of their moments of inertia I1 and I2 , respectively, about their axes is I1 : I2 = 1 : 16 then the value of $$\alpha $$ is :
I = $$M\left( {{{{R^2}} \over 4} + {{{L^2}} \over {12}}} \right)$$. If such a cylinder is to be made for a given mass of a material, the ratio $${L \over R}$$ for it to have minimum possible I is
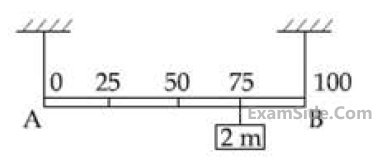
Shown in the figure is rigid and uniform one meter long rod AB held in horizontal position by two strings tied to its ends and attached to the ceiling. The rod is of mass ‘m’ and has another weight of mass 2 m hung at a distance of 75 cm from A. The tension in the string at A is :
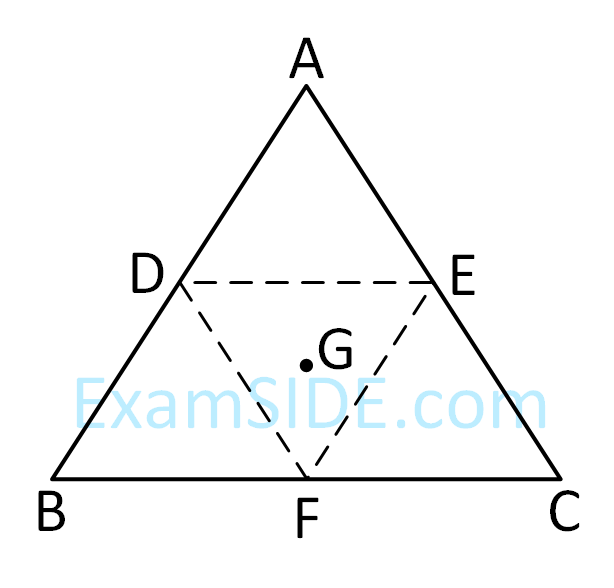
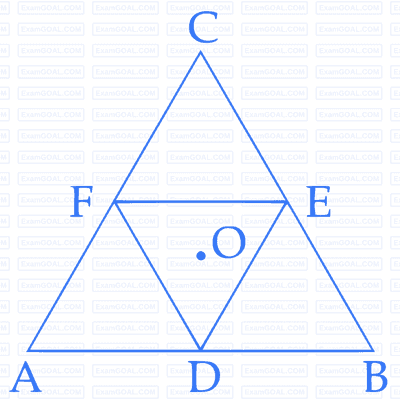
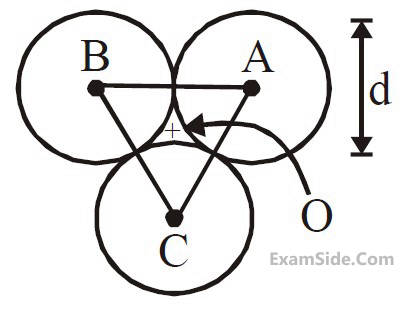 Three solid spheres each of mass m and
diameter d are stuck together such that the lines
connecting the centres form an equilateral
triangle of side of length d. The ratio I0/IA of
moment of inertia I0 of the system about an axis
passing the centroid and about center of any
of the spheres IA and perpendicular to the plane
of the triangle is :
Three solid spheres each of mass m and
diameter d are stuck together such that the lines
connecting the centres form an equilateral
triangle of side of length d. The ratio I0/IA of
moment of inertia I0 of the system about an axis
passing the centroid and about center of any
of the spheres IA and perpendicular to the plane
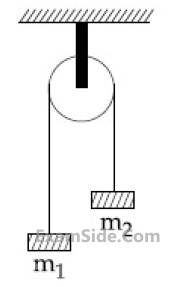
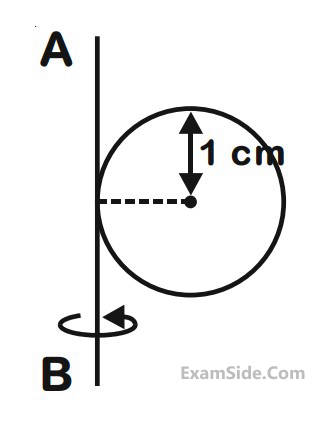
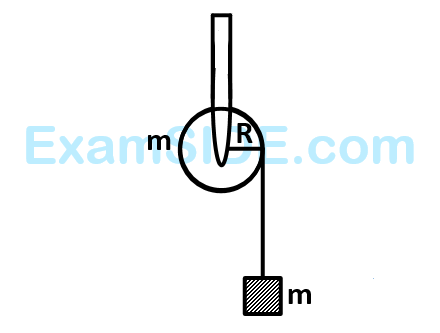
of the triangle is :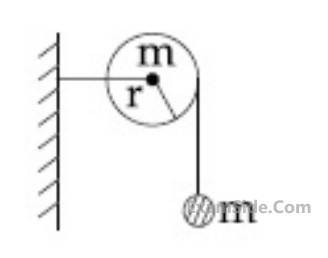 As shown in the figure, a bob of mass m is tied by a massless string whose other end portion is wound on a fly wheel (disc) of radius r and mass m. When released from rest the bob starts falling vertically. When it has covered a distance of h, the angular speed of the wheel will be:
As shown in the figure, a bob of mass m is tied by a massless string whose other end portion is wound on a fly wheel (disc) of radius r and mass m. When released from rest the bob starts falling vertically. When it has covered a distance of h, the angular speed of the wheel will be: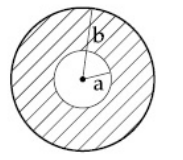
x = x0 + a cos$$\omega $$1t
y = y0 + b sin$$\omega $$2t
The torque, acting on the particle about the origin, at t = 0 is :

(Take g = 10 m/s2)


The relative velocity $${\overrightarrow V _A} - {\overrightarrow V _B}$$ at t = $${\pi \over {2\omega }}$$ is given by :
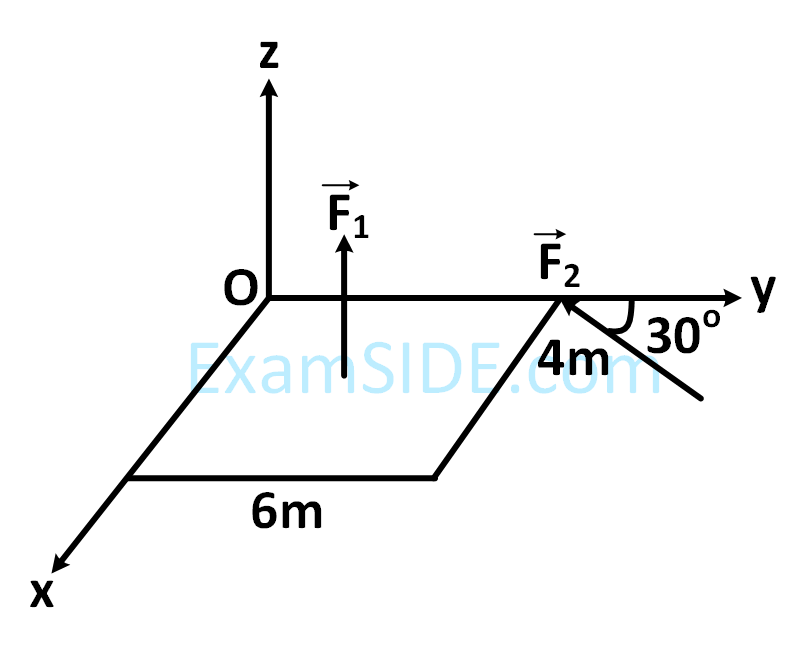
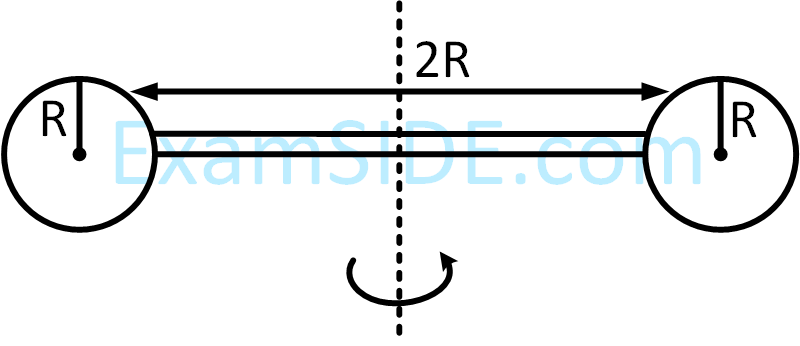


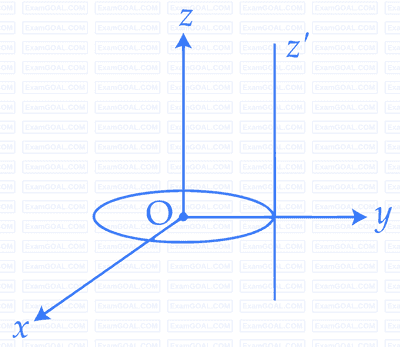
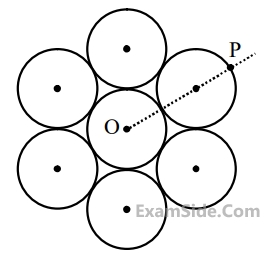
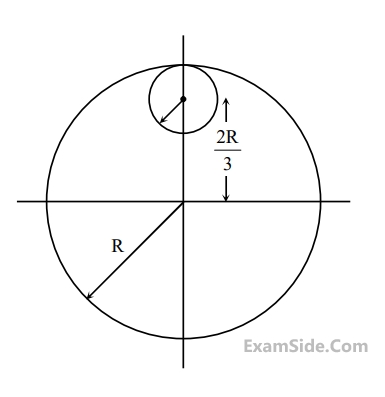



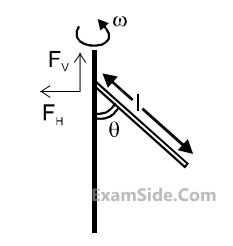
A uniform rod $$AB$$ is suspended from a point $$X,$$ at a variable distance $$x$$ from $$A$$, as shown, To make the rod horizontal, a mass $$m$$ is suspended from its end $$A.$$A$$ set of $$(m,x)$$ values is recorded. The appropriate variables that give a straight line, when plotted, are :


(Take the radius of the drum to be 1.25 m and its axle to be horizontal) :


where $$\widehat i,\widehat j$$ and $$\widehat k$$ are unit vectors along $$x,y$$ and $$z$$-axis respectively.
Numerical

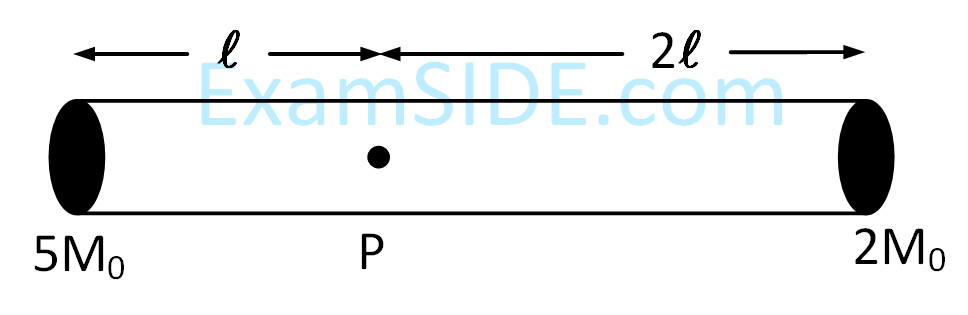
$\mathrm{A}, \mathrm{B}$ and C are disc, solid sphere and spherical shell respectively with same radii and masses. These masses are placed as shown in figure.

The moment of inertia of the given system about PQ axis is $\frac{x}{15} \mathrm{I}$, where I is the moment of inertia of the disc about its diameter. The value of $x$ is ____________.
A solid sphere with uniform density and radius $R$ is rotating initially with constant angular velocity $\left(\omega_1\right)$ about its diameter. After some time during the rotation its starts loosing mass at a uniform rate, with no change in its shape. The angular velocity of the sphere when its radius become $\mathrm{R} / 2$ is $x \omega_1$. The value of $x$ is _________.
A circular ring and a solid sphere having same radius roll down on an inclined plane from rest without slipping. The ratio of their velocities when reached at the bottom of the plane is $\sqrt{\frac{x}{5}}$ where $x=$ ________.

A wheel of radius 0.2 m rotates freely about its center when a string that is wrapped over its rim is pulled by force of 10 N as shown in figure. The established torque produces an angular acceleration of $2 \mathrm{rad} / \mathrm{s}^2$. Moment of intertia of the wheel is___________ $\mathrm{kg} \mathrm{}\,\, \mathrm{m}^2$. (Acceleration due to gravity $=10 \mathrm{~m} / \mathrm{s}^2$ )
The coordinates of a particle with respect to origin in a given reference frame is (1, 1, 1) meters. If a force of $\vec{F} = \hat{i} - \hat{j} + \hat{k}$ acts on the particle, then the magnitude of torque (with respect to origin) in z-direction is __________.
Two iron solid discs of negligible thickness have radii $R_1$ and $R_2$ and moment of intertia $I_1$ and $I_2$, respectively. For $R_2=2 R_1$, the ratio of $I_1$ and $I_2$ would be $1 / x$, where $\mathrm{x}=$ _______ .
The moment of inertia of a solid disc rotating along its diameter is 2.5 times higher than the moment of inertia of a ring rotating in similar way. The moment of inertia of a solid sphere which has same radius as the disc and rotating in similar way, is $n$ times higher than the moment of inertia of the given ring. Here, $\mathrm{n}=$ ________ Consider all the bodies have equal masses.
The position vectors of two 1 kg particles, (A) and (B), are given by $$ \overrightarrow{\mathrm{r}}_{\mathrm{A}}=\left(\alpha_1 \mathrm{t}^2 \hat{i}+\alpha_2 \mathrm{t} \hat{j}+\alpha_3 \mathrm{t} \hat{k}\right) \mathrm{m} \text { and } \overrightarrow{\mathrm{r}}_{\mathrm{B}}=\left(\beta_1 \hat{\mathrm{t}} \hat{i}+\beta_2 \mathrm{t}^2 \hat{j}+\beta_3 \mathrm{t} \hat{k}\right) \mathrm{m} \text {, respectively; } $$ $\left(\alpha_1=1 \mathrm{~m} / \mathrm{s}^2, \alpha_2=3 \mathrm{n} \mathrm{m} / \mathrm{s}, \alpha_3=2 \mathrm{~m} / \mathrm{s}, \beta_1=2 \mathrm{~m} / \mathrm{s}, \beta_2=-1 \mathrm{~m} / \mathrm{s}^2, \beta_3=4 \mathrm{pm} / \mathrm{s}\right)$, where t is time, n and $p$ are constants. At $t=1 \mathrm{~s},\left|\overrightarrow{V_A}\right|=\left|\overrightarrow{V_B}\right|$ and velocities $\vec{V}_A$ and $\vec{V}_B$ of the particles are orthogonal to each other. At $t=1 \mathrm{~s}$, the magnitude of angular momentum of particle (A) with respect to the position of particle (B) is $\sqrt{\mathrm{L}} \mathrm{kgm}^2 \mathrm{~s}^{-1}$. The value of L is _________.
A circular disc reaches from top to bottom of an inclined plane of length $$l$$. When it slips down the plane, if takes $$t \mathrm{~s}$$. When it rolls down the plane then it takes $$\left(\frac{\alpha}{2}\right)^{1 / 2} t \mathrm{~s}$$, where $$\alpha$$ is _________.
A string is wrapped around the rim of a wheel of moment of inertia $$0.40 \mathrm{~kgm}^2$$ and radius $$10 \mathrm{~cm}$$. The wheel is free to rotate about its axis. Initially the wheel is at rest. The string is now pulled by a force of $$40 \mathrm{~N}$$. The angular velocity of the wheel after $$10 \mathrm{~s}$$ is $$x \mathrm{~rad} / \mathrm{s}$$, where $$x$$ is __________.
A circular table is rotating with an angular velocity of $$\omega \mathrm{~rad} / \mathrm{s}$$ about its axis (see figure). There is a smooth groove along a radial direction on the table. A steel ball is gently placed at a distance of $$1 \mathrm{~m}$$ on the groove. All the surfaces are smooth. If the radius of the table is $$3 \mathrm{~m}$$, the radial velocity of the ball w.r.t. the table at the time ball leaves the table is $$x \sqrt{2} \omega \mathrm{~m} / \mathrm{s}$$, where the value of $$x$$ is _________.

Three balls of masses $$2 \mathrm{~kg}, 4 \mathrm{~kg}$$ and $$6 \mathrm{~kg}$$ respectively are arranged at centre of the edges of an equilateral triangle of side $$2 \mathrm{~m}$$. The moment of inertia of the system about an axis through the centroid and perpendicular to the plane of triangle, will be ________ $$\mathrm{kg} \mathrm{~m}^2$$.
A hollow sphere is rolling on a plane surface about its axis of symmetry. The ratio of rotational kinetic energy to its total kinetic energy is $$\frac{x}{5}$$. The value of $$x$$ is _________.
A solid sphere and a hollow cylinder roll up without slipping on same inclined plane with same initial speed $$v$$. The sphere and the cylinder reaches upto maximum heights $$h_1$$ and $$h_2$$ respectively, above the initial level. The ratio $$h_1: h_2$$ is $$\frac{n}{10}$$. The value of $$n$$ is __________.
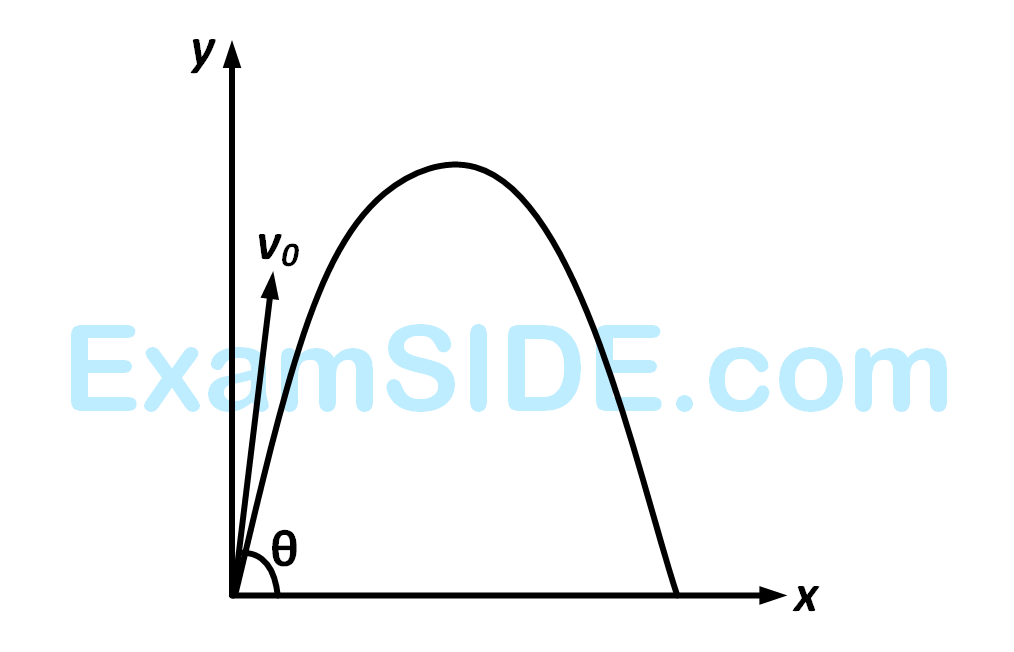
A body of mass '$$m$$' is projected with a speed '$$u$$' making an angle of $$45^{\circ}$$ with the ground. The angular momentum of the body about the point of projection, at the highest point is expressed as $$\frac{\sqrt{2} m u^3}{X g}$$. The value of '$$X$$' is _________.
Two identical spheres each of mass $$2 \mathrm{~kg}$$ and radius $$50 \mathrm{~cm}$$ are fixed at the ends of a light rod so that the separation between the centers is $$150 \mathrm{~cm}$$. Then, moment of inertia of the system about an axis perpendicular to the rod and passing through its middle point is $$\frac{x}{20} \mathrm{~kg} \mathrm{m^{2 }}$$, where the value of $$x$$ is ___________.
Two discs of moment of inertia $$I_1=4 \mathrm{~kg} \mathrm{~m}^2$$ and $$I_2=2 \mathrm{~kg} \mathrm{~m}^2$$, about their central axes & normal to their planes, rotating with angular speeds $$10 \mathrm{~rad} / \mathrm{s}$$ & $$4 \mathrm{~rad} / \mathrm{s}$$ respectively are brought into contact face to face with their axes of rotation coincident. The loss in kinetic energy of the system in the process is _________ J.

Consider a Disc of mass $$5 \mathrm{~kg}$$, radius $$2 \mathrm{~m}$$, rotating with angular velocity of $$10 \mathrm{~rad} / \mathrm{s}$$ about an axis perpendicular to the plane of rotation. An identical disc is kept gently over the rotating disc along the same axis. The energy dissipated so that both the discs continue to rotate together without slipping is ________ J.
A body of mass $$5 \mathrm{~kg}$$ moving with a uniform speed $$3 \sqrt{2} \mathrm{~ms}^{-1}$$ in $$X-Y$$ plane along the line $$y=x+4$$. The angular momentum of the particle about the origin will be _________ $$\mathrm{kg} \mathrm{~m}^2 \mathrm{~s}^{-1}$$.
A cylinder is rolling down on an inclined plane of inclination $$60^{\circ}$$. It's acceleration during rolling down will be $$\frac{x}{\sqrt{3}} m / s^2$$, where $$x=$$ ________ (use $$\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$$).
A ring and a solid sphere roll down the same inclined plane without slipping. They start from rest. The radii of both bodies are identical and the ratio of their kinetic energies is $$\frac{7}{x}$$, where $$x$$ is _________.
Four particles each of mass $$1 \mathrm{~kg}$$ are placed at four corners of a square of side $$2 \mathrm{~m}$$. Moment of inertia of system about an axis perpendicular to its plane and passing through one of its vertex is _____ $$\mathrm{kgm}^2$$.

A light rope is wound around a hollow cylinder of mass 5 kg and radius 70 cm. The rope is pulled with a force of 52.5 N. The angular acceleration of the cylinder will be _________ rad s$$^{-2}$$.
A solid sphere is rolling on a horizontal plane without slipping. If the ratio of angular momentum about axis of rotation of the sphere to the total energy of moving sphere is $$\pi: 22$$ then, the value of its angular speed will be ____________ $$\mathrm{rad} / \mathrm{s}$$.
For a rolling spherical shell, the ratio of rotational kinetic energy and total kinetic energy is $$\frac{x}{5}$$. The value of $$x$$ is ___________.
A circular plate is rotating in horizontal plane, about an axis passing through its center and perpendicular to the plate, with an angular velocity $$\omega$$. A person sits at the center having two dumbbells in his hands. When he stretches out his hands, the moment of inertia of the system becomes triple. If E be the initial Kinetic energy of the system, then final Kinetic energy will be $$\frac{E}{x}$$. The value of $$x$$ is
A solid sphere of mass $$500 \mathrm{~g}$$ and radius $$5 \mathrm{~cm}$$ is rotated about one of its diameter with angular speed of $$10 ~\mathrm{rad} ~\mathrm{s}^{-1}$$. If the moment of inertia of the sphere about its tangent is $$x \times 10^{-2}$$ times its angular momentum about the diameter. Then the value of $$x$$ will be ___________.
A force of $$-\mathrm{P} \hat{\mathrm{k}}$$ acts on the origin of the coordinate system. The torque about the point $$(2,-3)$$ is $$\mathrm{P}(a \hat{i}+b \hat{j})$$, The ratio of $$\frac{a}{b}$$ is $$\frac{x}{2}$$. The value of $$x$$ is -
A hollow spherical ball of uniform density rolls up a curved surface with an initial velocity $$3 \mathrm{~m} / \mathrm{s}$$ (as shown in figure). Maximum height with respect to the initial position covered by it will be __________ cm.

The moment of inertia of a semicircular ring about an axis, passing through the center and perpendicular to the plane of ring, is $$\frac{1}{x} \mathrm{MR}^{2}$$, where $$\mathrm{R}$$ is the radius and $$M$$ is the mass of the semicircular ring. The value of $$x$$ will be __________.
A ring and a solid sphere rotating about an axis passing through their centers have same radii of gyration. The axis of rotation is perpendicular to plane of ring. The ratio of radius of ring to that of sphere is $$\sqrt{\frac{2}{x}}$$. The value of $$x$$ is ___________.
Two identical solid spheres each of mass $$2 \mathrm{~kg}$$ and radii $$10 \mathrm{~cm}$$ are fixed at the ends of a light rod. The separation between the centres of the spheres is $$40 \mathrm{~cm}$$. The moment of inertia of the system about an axis perpendicular to the rod passing through its middle point is __________ $$\times 10^{-3} \mathrm{~kg}~\mathrm{m}^{2}$$
Moment of inertia of a disc of mass '$$M$$' and radius '$$R$$' about any of its diameter is $$\frac{M R^{2}}{4}$$. The moment of inertia of this disc about an axis normal to the disc and passing through a point on its edge will be, $$\frac{x}{2}$$ MR$$^{2}$$. The value of $$x$$ is ___________.
A solid cylinder is released from rest from the top of an inclined plane of inclination $$30^{\circ}$$ and length $$60 \mathrm{~cm}$$. If the cylinder rolls without slipping, its speed upon reaching the bottom of the inclined plane is __________ $$\mathrm{ms}^{-1}$$. (Given $$\mathrm{g}=10 \mathrm{~ms}^{-2}$$)

A solid sphere of mass $$1 \mathrm{~kg}$$ rolls without slipping on a plane surface. Its kinetic energy is $$7 \times 10^{-3} \mathrm{~J}$$. The speed of the centre of mass of the sphere is __________ $$\operatorname{cm~s}^{-1}$$
A uniform disc of mass $0.5 \mathrm{~kg}$ and radius $r$ is projected with velocity $18 \mathrm{~m} / \mathrm{s}$ at $\mathrm{t}=0$ s on a rough horizontal surface. It starts off with a purely sliding motion at $\mathrm{t}=0 \mathrm{~s}$. After $2 \mathrm{~s}$ it acquires a purely rolling motion (see figure). The total kinetic energy of the disc after $2 \mathrm{~s}$ will be __________ $\mathrm{J}$ (given, coefficient of friction is $0.3$ and $g=10 \mathrm{~m} / \mathrm{s}^{2}$ ).

A thin uniform rod of length $$2 \mathrm{~m}$$, cross sectional area '$$A$$' and density '$$\mathrm{d}$$' is rotated about an axis passing through the centre and perpendicular to its length with angular velocity $$\omega$$. If value of $$\omega$$ in terms of its rotational kinetic energy $$E$$ is $$\sqrt{\frac{\alpha E}{A d}}$$ then value of $$\alpha$$ is ______________.
A particle of mass 100 g is projected at time t = 0 with a speed 20 ms$$^{-1}$$ at an angle 45$$^\circ$$ to the horizontal as given in the figure. The magnitude of the angular momentum of the particle about the starting point at time t = 2s is found to be $$\mathrm{\sqrt K~kg~m^2/s}$$. The value of K is ___________.
(Take g = 10 ms$$^{-2}$$)

A solid sphere of mass 2 kg is making pure rolling on a horizontal surface with kinetic energy 2240 J. The velocity of centre of mass of the sphere will be _______ ms$$^{-1}$$.
If a solid sphere of mass 5 kg and a disc of mass 4 kg have the same radius. Then the ratio of moment of inertia of the disc about a tangent in its plane to the moment of inertia of the sphere about its tangent will be $$\frac{x}{7}$$. The value of $$x$$ is ___________.
$$\mathrm{I_{CM}}$$ is the moment of inertia of a circular disc about an axis (CM) passing through its center and perpendicular to the plane of disc. $$\mathrm{I_{AB}}$$ is it's moment of inertia about an axis AB perpendicular to plane and parallel to axis CM at a distance $$\frac{2}{3}$$R from center. Where R is the radius of the disc. The ratio of $$\mathrm{I_{AB}}$$ and $$\mathrm{I_{CM}}$$ is $$x:9$$. The value of $$x$$ is _____________.

A uniform solid cylinder with radius R and length L has moment of inertia I$$_1$$, about the axis of the cylinder. A concentric solid cylinder of radius $$R'=\frac{R}{2}$$ and length $$L'=\frac{L}{2}$$ is carved out of the original cylinder. If I$$_2$$ is the moment of inertia of the carved out portion of the cylinder then $$\frac{I_1}{I_2}=$$ __________.
(Both I$$_1$$ and I$$_2$$ are about the axis of the cylinder)
Solid sphere A is rotating about an axis PQ. If the radius of the sphere is 5 cm then its radius of gyration about PQ will be $$\sqrt x$$ cm. The value of $$x$$ is ________.

Four identical discs each of mass '$$\mathrm{M}$$' and diameter '$$\mathrm{a}$$' are arranged in a small plane as shown in figure. If the moment of inertia of the system about $$\mathrm{OO}^{\prime}$$ is $$\frac{x}{4} \,\mathrm{Ma}^{2}$$. Then, the value of $$x$$ will be ____________.

A solid cylinder length is suspended symmetrically through two massless strings, as shown in the figure. The distance from the initial rest position, the cylinder should be unbinding the strings to achieve a speed of $$4 \mathrm{~ms}^{-1}$$, is ____________ cm. (take g = $$10 \mathrm{~ms}^{-2}$$)

A pulley of radius $$1.5 \mathrm{~m}$$ is rotated about its axis by a force $$F=\left(12 \mathrm{t}-3 \mathrm{t}^{2}\right) N$$ applied tangentially (while t is measured in seconds). If moment of inertia of the pulley about its axis of rotation is $$4.5 \mathrm{~kg} \mathrm{~m}^{2}$$, the number of rotations made by the pulley before its direction of motion is reversed, will be $$\frac{K}{\pi}$$. The value of K is ___________.
The radius of gyration of a cylindrical rod about an axis of rotation perpendicular to its length and passing through the center will be ___________ $$\mathrm{m}$$.
Given, the length of the rod is $$10 \sqrt{3} \mathrm{~m}$$.
A disc of mass $$1 \mathrm{~kg}$$ and radius $$\mathrm{R}$$ is free to rotate about a horizontal axis passing through its centre and perpendicular to the plane of disc. A body of same mass as that of disc is fixed at the highest point of the disc. Now the system is released, when the body comes to the lowest position, its angular speed will be $$4 \sqrt{\frac{x}{3 R}} \,\operatorname{rad}{s}^{-1}$$ where $$x=$$ ____________. $$\left(g=10 \mathrm{~ms}^{-2}\right)$$
Four particles with a mass of 1 kg, 2 kg, 3 kg and 4 kg are situated at the corners of a square with side 1 m (as shown in the figure). The moment of inertia of the system, about an axis passing through the point O and perpendicular to the plane of the square, is ______________ kg m2.

The moment of inertia of a uniform thin rod about a perpendicular axis passing through one end is I1. The same rod is bent into a ring and its moment of inertia about a diameter is I2. If $${{{I_1}} \over {{I_2}}}$$ is $${{x{\pi ^2}} \over 3}$$, then the value of x will be ____________.
A uniform disc with mass M = 4 kg and radius R = 10 cm is mounted on a fixed horizontal axle as shown in figure. A block with mass m = 2 kg hangs from a massless cord that is wrapped around the rim of the disc. During the fall of the block, the cord does not slip and there is no friction at the axle. The tension in the cord is ____________ N.
(Take g = 10 ms$$-$$2)

The position vector of 1 kg object is $$\overrightarrow r = \left( {3\widehat i - \widehat j} \right)m$$ and its velocity $$\overrightarrow v = \left( {3\widehat j + \widehat k} \right)m{s^{ - 1}}$$. The magnitude of its angular momentum is $$\sqrt x $$ Nm where x is ___________.
A rolling wheel of 12 kg is on an inclined plane at position P and connected to a mass of 3 kg through a string of fixed length and pulley as shown in figure. Consider PR as friction free surface. The velocity of centre of mass of the wheel when it reaches at the bottom Q of the inclined plane PQ will be $${1 \over 2}\sqrt {xgh} $$ m/s. The value of x is ___________.

Moment of Inertia (M.I.) of four bodies having same mass 'M' and radius '2R' are as follows:
I1 = M.I. of solid sphere about its diameter
I2 = M.I. of solid cylinder about its axis
I3 = M.I. of solid circular disc about its diameter
I4 = M.I. of thin circular ring about its diameter
If 2(I2 + I3) + I4 = x . I1, then the value of x will be __________.
A metre scale is balanced on a knife edge at its centre. When two coins, each of mass 10 g are put one on the top of the other at the 10.0 cm mark the scale is found to be balanced at 40.0 cm mark. The mass of the metre scale is found to be x $$\times$$ 10$$-$$2 kg. The value of x is ___________.
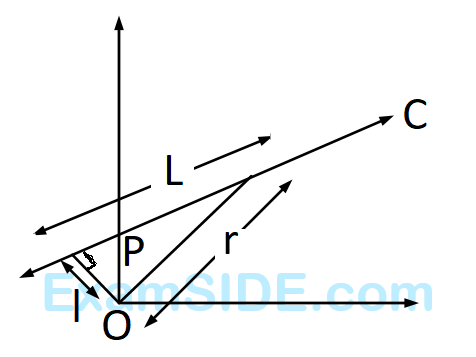
If the mass of the linear and circular portions of the badminton racket are same (M) and the mass of the threads are negligible, the moment of inertia of the racket about an axis perpendicular to the handle and in the plane of the ring at, $${r \over 2}$$ distance from the end A of the handle will be ................ Mr2.

$$\overrightarrow r = 10\alpha {t^2}\widehat i + 5\beta (t - 5)\widehat j$$
Where $$\alpha$$ and $$\beta$$ are dimensional constants.
The angular momentum of the particle becomes the same as it was for t = 0 at time t = ____________ seconds.
(1) a ring
(2) a disc
(3) a solid cylinder
(4) a solid sphere,
of same mass 'm' and radius 'R' are allowed to roll down without slipping simultaneously from the top of the inclined plane. The body which will reach first at the bottom of the inclined plane is ___________. [Mark the body as per their respective numbering given in the question]


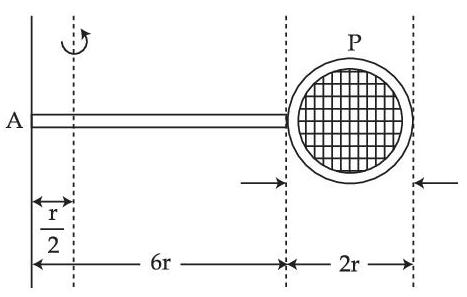
Suppose the disk makes n number of revolutions to attain an angular speed of 50 rad s$$-$$1.
The value of n, to the nearest integer, is __________.
[Given : In one complete revolution, the disk rotates by 6.28 rad]

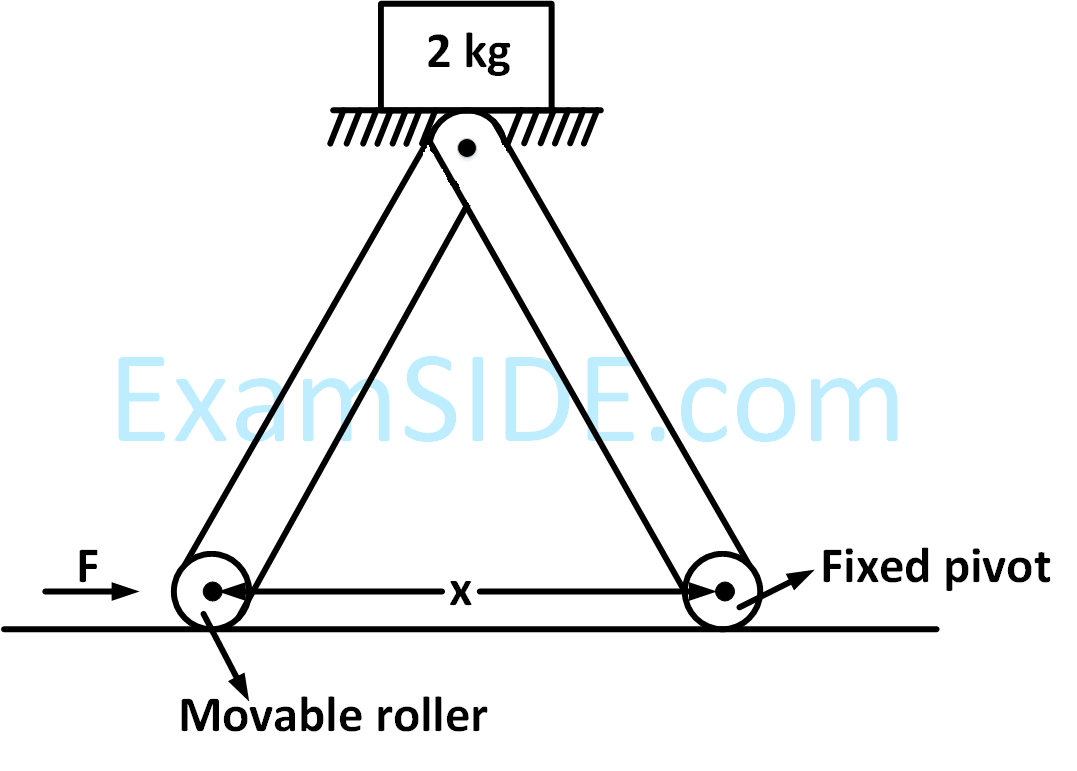
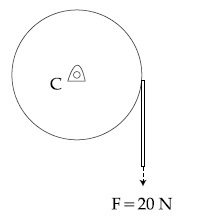
Suppose the force is $$\overrightarrow P $$ resolved parallel to the arms AB and AC of the frame.
The magnitude of the resolved component along the arm AC is xN.
The value of x, to the nearest integer, is ___________.
[Given : sin(35$$^\circ$$) = 0.573, cos(35$$^\circ$$) = 0.819
sin(110$$^\circ$$) = 0.939, cos(110$$^\circ$$) = $$-$$ 0.342 J

$$\left( {4\widehat i + 3\widehat j - \widehat k} \right)$$ m. Then the magnitude of torque
about the point $$\left( {\widehat i + 2\widehat j + \widehat k} \right)$$ m will be $$\sqrt x $$ N m.
The value of x is _______.
(Breaking stress of wire = 4.8 × 107 Nm–2 and
area of cross-section of the wire = 10–2 cm2) is:
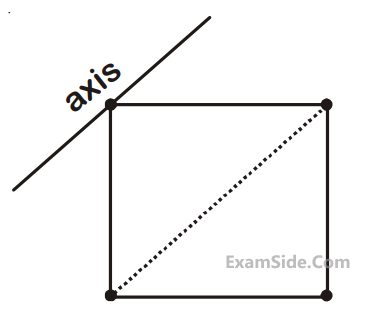
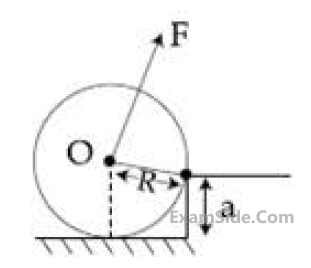
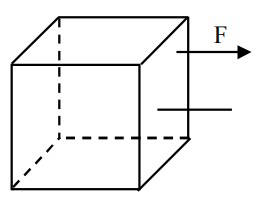 Consider a uniform cubical box of side a on a rough floor that is to be moved by applying
minimum possible force F at a point b above its centre of mass (see figure). If the coefficient of
friction is $$\mu $$ = 0.4, the maximum possible value of 100 × $${b \over a}$$
for box not to topple before moving
is .......
Consider a uniform cubical box of side a on a rough floor that is to be moved by applying
minimum possible force F at a point b above its centre of mass (see figure). If the coefficient of
friction is $$\mu $$ = 0.4, the maximum possible value of 100 × $${b \over a}$$
for box not to topple before moving
is .......