Alternating Current · Physics · JEE Main
Numerical
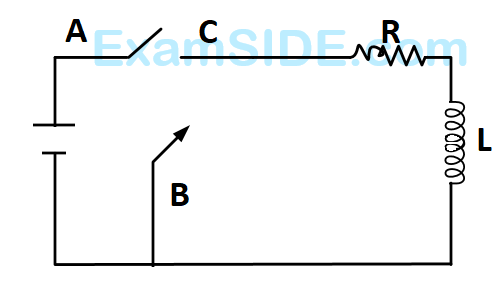
For ac circuit shown in figure, $\mathrm{R}=100 \mathrm{k} \Omega$ and $\mathrm{C}=100 \mathrm{pF}$ and the phase difference between $\mathrm{V}_{\text {in }}$ and $\left(\mathrm{V}_{\mathrm{B}}-\mathrm{V}_{\mathrm{A}}\right)$ is $90^{\circ}$. The input signal frequency is $10^x \mathrm{rad} / \mathrm{sec}$, where ' $x$ ' is __________ .

An inductor of self inductance 1 H is connected in series with a resistor of $100 \pi$ ohm and an ac supply of $100 \pi$ volt, 50 Hz . Maximum current flowing in the circuit is _________ A.
In a series LCR circuit, a resistor of $300 \Omega$, a capacitor of 25 nF and an inductor of 100 mH are used. For maximum current in the circuit, the angular frequency of the ac source is _________ $\times 10^4$ radians $\mathrm{s}^{-1}$
A capacitor of reactance $$4 \sqrt{3} \Omega$$ and a resistor of resistance $$4 \Omega$$ are connected in series with an ac source of peak value $$8 \sqrt{2} \mathrm{~V}$$. The power dissipation in the circuit is __________ W.
When a coil is connected across a $$20 \mathrm{~V}$$ dc supply, it draws a current of $$5 \mathrm{~A}$$. When it is connected across $$20 \mathrm{~V}, 50 \mathrm{~Hz}$$ ac supply, it draws a current of $$4 \mathrm{~A}$$. The self inductance of the coil is __________ $$\mathrm{mH}$$. (Take $$\pi=3$$)
An alternating emf $$\mathrm{E}=110 \sqrt{2} \sin 100 \mathrm{t}$$ volt is applied to a capacitor of $$2 \mu \mathrm{F}$$, the rms value of current in the circuit is ________ $$\mathrm{mA}$$.
For a given series LCR circuit it is found that maximum current is drawn when value of variable capacitance is $$2.5 \mathrm{~nF}$$. If resistance of $$200 \Omega$$ and $$100 \mathrm{~mH}$$ inductor is being used in the given circuit. The frequency of ac source is _________ $$\times 10^3 \mathrm{~Hz}$$ (given $$\mathrm{a}^2=10$$)
When a $$d c$$ voltage of $$100 \mathrm{~V}$$ is applied to an inductor, a $$d c$$ current of $$5 \mathrm{~A}$$ flows through it. When an ac voltage of $$200 \mathrm{~V}$$ peak value is connected to inductor, its inductive reactance is found to be $$20 \sqrt{3} \Omega$$. The power dissipated in the circuit is _________ W.
An ac source is connected in given series LCR circuit. The rms potential difference across the capacitor of $$20 \mu \mathrm{F}$$ is __________ V.

A alternating current at any instant is given by $$i=[6+\sqrt{56} \sin (100 \pi t+\pi / 3)]$$ A. The $$r m s$$ value of the current is ______ A.
A power transmission line feeds input power at $$2.3 \mathrm{~kV}$$ to a step down transformer with its primary winding having 3000 turns. The output power is delivered at $$230 \mathrm{~V}$$ by the transformer. The current in the primary of the transformer is $$5 \mathrm{~A}$$ and its efficiency is $$90 \%$$. The winding of transformer is made of copper. The output current of transformer is _________ $$A$$.
A series LCR circuit with $$\mathrm{L}=\frac{100}{\pi} \mathrm{mH}, \mathrm{C}=\frac{10^{-3}}{\pi} \mathrm{F}$$ and $$\mathrm{R}=10 \Omega$$, is connected across an ac source of $$220 \mathrm{~V}, 50 \mathrm{~Hz}$$ supply. The power factor of the circuit would be ________.
In the given figure, an inductor and a resistor are connected in series with a battery of emf E volt. $$\frac{E^{a}}{2 b} \mathrm{~J} / s$$ represents the maximum rate at which the energy is stored in the magnetic field (inductor). The numerical value of $$\frac{b}{a}$$ will be __________.

A coil has an inductance of $$2 \mathrm{H}$$ and resistance of $$4 ~\Omega$$. A $$10 \mathrm{~V}$$ is applied across the coil. The energy stored in the magnetic field after the current has built up to its equilibrium value will be ___________ $$\times 10^{-2} \mathrm{~J}$$.
A series combination of resistor of resistance $$100 ~\Omega$$, inductor of inductance $$1 ~\mathrm{H}$$ and capacitor of capacitance $$6.25 ~\mu \mathrm{F}$$ is connected to an ac source. The quality factor of the circuit will be __________
An oscillating LC circuit consists of a $$75 ~\mathrm{mH}$$ inductor and a $$1.2 ~\mu \mathrm{F}$$ capacitor. If the maximum charge to the capacitor is $$2.7 ~\mu \mathrm{C}$$. The maximum current in the circuit will be ___________ $$\mathrm{mA}$$
An ideal transformer with purely resistive load operates at $$12 ~\mathrm{kV}$$ on the primary side. It supplies electrical energy to a number of nearby houses at $$120 \mathrm{~V}$$. The average rate of energy consumption in the houses served by the transformer is 60 $$\mathrm{kW}$$. The value of resistive load $$(\mathrm{Rs})$$ required in the secondary circuit will be ___________ $$\mathrm{m} \Omega$$.
A square shaped coil of area $$70 \mathrm{~cm}^{2}$$ having 600 turns rotates in a magnetic field of $$0.4 ~\mathrm{wbm}^{-2}$$, about an axis which is parallel to one of the side of the coil and perpendicular to the direction of field. If the coil completes 500 revolution in a minute, the instantaneous emf when the plane of the coil is inclined at $$60^{\circ}$$ with the field, will be ____________ V. (Take $$\pi=\frac{22}{7}$$)
A series LCR circuit is connected to an ac source of $$220 \mathrm{~V}, 50 \mathrm{~Hz}$$. The circuit contain a resistance $$\mathrm{R}=100 ~\Omega$$ and an inductor of inductive reactance $$\mathrm{X}_{\mathrm{L}}=79.6 ~\Omega$$. The capacitance of the capacitor needed to maximize the average rate at which energy is supplied will be _________ $$\mu \mathrm{F}$$.
voltage is 2500 $\cos (100 \pi \mathrm{t}) \mathrm{V}$. The amplitude of current, in the circuit, is _________ A.
An inductor of $$0.5 ~\mathrm{mH}$$, a capacitor of $$20 ~\mu \mathrm{F}$$ and resistance of $$20 ~\Omega$$ are connected in series with a $$220 \mathrm{~V}$$ ac source. If the current is in phase with the emf, the amplitude of current of the circuit is $$\sqrt{x}$$ A. The value of $$x$$ is ___________
$\left(\right.$ Take $\left.\pi=\frac{22}{7}\right)$
An inductor of inductance 2 $$\mathrm{\mu H}$$ is connected in series with a resistance, a variable capacitor and an AC source of frequency 7 kHz. The value of capacitance for which maximum current is drawn into the circuit $$\frac{1}{x}\mathrm{F}$$, where the value of $$x$$ is ___________.
(Take $$\pi=\frac{22}{7}$$)
A series LCR circuit is connected to an AC source of 220 V, 50 Hz. The circuit contains a resistance R = 80$$\Omega$$, an inductor of inductive reactance $$\mathrm{X_L=70\Omega}$$, and a capacitor of capacitive reactance $$\mathrm{X_C=130\Omega}$$. The power factor of circuit is $$\frac{x}{10}$$. The value of $$x$$ is :
An LCR series circuit of capacitance 62.5 nF and resistance of 50 $$\Omega$$, is connected to an A.C. source of frequency 2.0 kHz. For maximum value of amplitude of current in circuit, the value of inductance is __________ mH.
(Take $$\pi^2=10$$)
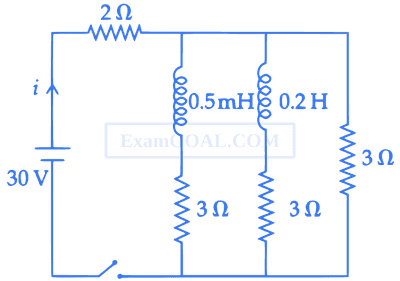
In the circuit shown in the figure, the ratio of the quality factor and the band width is ___________ s.

A capacitor of capacitance 500 $$\mu$$F is charged completely using a dc supply of 100 V. It is now connected to an inductor of inductance 50 mH to form an LC circuit. The maximum current in LC circuit will be _______ A.
The frequencies at which the current amplitude in an LCR series circuit becomes $$\frac{1}{\sqrt{2}}$$ times its maximum value, are $$212\,\mathrm{rad} \,\mathrm{s}^{-1}$$ and $$232 \,\mathrm{rad} \,\mathrm{s}^{-1}$$. The value of resistance in the circuit is $$R=5 \,\Omega$$. The self inductance in the circuit is __________ $$\mathrm{mH}$$.
To light, a $$50 \mathrm{~W}, 100 \mathrm{~V}$$ lamp is connected, in series with a capacitor of capacitance $$\frac{50}{\pi \sqrt{x}} \mu F$$, with $$200 \mathrm{~V}, 50 \mathrm{~Hz} \,\mathrm{AC}$$ source. The value of $$x$$ will be ___________.
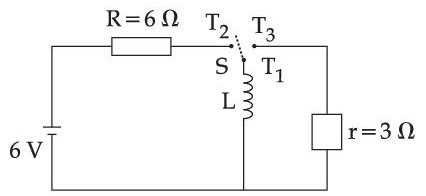
The effective current I in the given circuit at very high frequencies will be ___________ A.

A series LCR circuit with $$R = {{250} \over {11}}\,\Omega $$ and $${X_L} = {{70} \over {11}}\,\Omega $$ is connected across a 220 V, 50 Hz supply. The value of capacitance needed to maximize the average power of the circuit will be _________ $$\mu$$F. (Take : $$\pi = {{22} \over 7}$$)
An inductor of 0.5 mH, a capacitor of 200 $$\mu$$F and a resistor of 2 $$\Omega$$ are connected in series with a 220 V ac source. If the current is in phase with the emf, the frequency of ac source will be ____________ $$\times$$ 102 Hz.
In the given circuit, the magnitude of VL and VC are twice that of VR. Given that f = 50 Hz, the inductance of the coil is $${1 \over {K\pi }}$$ mH. The value of K is ____________.

An AC source is connected to an inductance of 100 mH, a capacitance of 100 $$\mu$$F and a resistance of 120 $$\Omega$$ as shown in figure. The time in which the resistance having a thermal capacity 2 J/$$^\circ$$C will get heated by 16$$^\circ$$C is _____________ s.

A telegraph line of length 100 km has a capacity of 0.01 $$\mu$$F/km and it carries an alternating current at 0.5 kilo cycle per second. If minimum impedance is required, then the value of the inductance that needs to be introduced in series is _____________ mH. (if $$\pi$$ = $$\sqrt{10}$$)
A 220 V, 50 Hz AC source is connected to a 25 V, 5 W lamp and an additional resistance R in series (as shown in figure) to run the lamp at its peak brightness, then the value of R (in ohm) will be _____________.

A 110 V, 50 Hz, AC source is connected in the circuit (as shown in figure). The current through the resistance 55 $$\Omega$$, at resonance in the circuit, will be __________ A.

In a series LCR circuit, the inductance, capacitance and resistance are L = 100 mH, C = 100 $$\mu$$F and R = 10 $$\Omega$$ respectively. They are connected to an AC source of voltage 220 V and frequency of 50 Hz. The approximate value of current in the circuit will be ___________ A.

As shown in the figure an inductor of inductance 200 mH is connected to an AC source of emf 220 V and frequency 50 Hz. The instantaneous voltage of the source is 0 V when the peak value of current is $${{\sqrt a } \over \pi }$$ A. The value of $$a$$ is ___________.

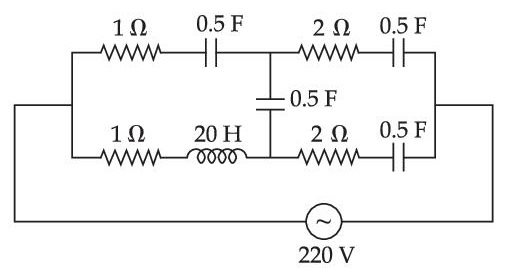
The r.m.s. value of of this current is ................. A.
MCQ (Single Correct Answer)
An ac current is represented as
$$i=5 \sqrt{2}+10 \cos \left(650 \pi t+\frac{\pi}{6}\right) A m p$$
The r.m.s value of the current is
An alternating current is represented by the equation, $i=100 \sqrt{2} \sin (100 \pi t)$ ampere. The RMS value of current and the frequency of the given alternating current are
An alternating current is given by $\mathrm{I}=\mathrm{I}_{\mathrm{A}} \sin \omega \mathrm{t}+\mathrm{I}_{\mathrm{B}} \cos \omega \mathrm{t}$. The r.m.s current will be
A series LCR circuit is connected to an alternating source of emf E. The current amplitude at resonant frequency is $I_0$. If the value of resistance R becomes twice of its initial value then amplitude of current at resonance will be
A bulb and a capacitor are connected in series across an ac supply. A dielectric is then placed between the plates of the capacitor. The glow of the bulb :
A coil of negligible resistance is connected in series with $$90 \Omega$$ resistor across $$120 \mathrm{~V}, 60 \mathrm{~Hz}$$ supply. A voltmeter reads $$36 \mathrm{~V}$$ across resistance. Inductance of the coil is :
A LCR circuit is at resonance for a capacitor C, inductance L and resistance R. Now the value of resistance is halved keeping all other parameters same. The current amplitude at resonance will be now:
Given below are two statements :
Statement I : In an LCR series circuit, current is maximum at resonance.
Statement II : Current in a purely resistive circuit can never be less than that in a series LCR circuit when connected to same voltage source.
In the light of the above statements, choose the correct from the options given below :
A series LCR circuit is subjected to an ac signal of $$200 \mathrm{~V}, 50 \mathrm{~Hz}$$. If the voltage across the inductor $$(\mathrm{L}=10 \mathrm{~mH})$$ is $$31.4 \mathrm{~V}$$, then the current in this circuit is _______.
An alternating voltage of amplitude $$40 \mathrm{~V}$$ and frequency $$4 \mathrm{~kHz}$$ is applied directly across the capacitor of $$12 \mu \mathrm{F}$$. The maximum displacement current between the plates of the capacitor is nearly :
Match List I with List II
| LIST I | LIST II |
||
|---|---|---|---|
| A. | Purely capacitive circuit | I. |  |
| B. | Purely inductive circuit | II. |  |
| C. | LCR series at resonance | III. |  |
| D. | LCR series circuit | IV. |  |
Choose the correct answer from the options given below:
In an ac circuit, the instantaneous current is zero, when the instantaneous voltage is maximum. In this case, the source may be connected to :
A. pure inductor.
B. pure capacitor.
C. pure resistor.
D. combination of an inductor and capacitor.
Choose the correct answer from the options given below :
An AC voltage $$V=20 \sin 200 \pi t$$ is applied to a series LCR circuit which drives a current $$I=10 \sin \left(200 \pi t+\frac{\pi}{3}\right)$$. The average power dissipated is:
An alternating voltage $$V(t)=220 \sin 100 \pi t$$ volt is applied to a purely resistive load of $$50 \Omega$$. The time taken for the current to rise from half of the peak value to the peak value is:
Primary coil of a transformer is connected to $$220 \mathrm{~V}$$ ac. Primary and secondary turns of the transforms are 100 and 10 respectively. Secondary coil of transformer is connected to two series resistances shown in figure. The output voltage $$\left(V_0\right)$$ is :

A series L.R circuit connected with an ac source $$E=(25 \sin 1000 t) V$$ has a power factor of $$\frac{1}{\sqrt{2}}$$. If the source of emf is changed to $$\mathrm{E}=(20 \sin 2000 \mathrm{t}) \mathrm{V}$$, the new power factor of the circuit will be :
In an a.c. circuit, voltage and current are given by:
$$V=100 \sin (100 t) V$$ and $$I=100 \sin \left(100 t+\frac{\pi}{3}\right) \mathrm{mA}$$ respectively.
The average power dissipated in one cycle is:
A capacitor of capacitance $$100 \mu \mathrm{F}$$ is charged to a potential of $$12 \mathrm{~V}$$ and connected to a $$6.4 \mathrm{~mH}$$ inductor to produce oscillations. The maximum current in the circuit would be :
Primary side of a transformer is connected to $$230 \mathrm{~V}, 50 \mathrm{~Hz}$$ supply. Turns ratio of primary to secondary winding is $$10: 1$$. Load resistance connected to secondary side is $$46 \Omega$$. The power consumed in it is :
Given below are two statements:
Statement I : An AC circuit undergoes electrical resonance if it contains either a capacitor or an inductor.
Statement II : An AC circuit containing a pure capacitor or a pure inductor consumes high power due to its non-zero power factor.
In the light of above statements, choose the correct answer form the options given below:
Given below are two statements:
Statement I : When the frequency of an a.c source in a series LCR circuit increases, the current in the circuit first increases, attains a maximum value and then decreases.
Statement II : In a series LCR circuit, the value of power factor at resonance is one.
In the light of given statements, choose the most appropriate answer from the options given below.

As per the given graph, choose the correct representation for curve $$\mathrm{A}$$ and curve B.
Where $$\mathrm{X}_{\mathrm{C}}=$$ reactance of pure capacitive circuit connected with A.C. source
$$\mathrm{X}_{\mathrm{L}}=$$ reactance of pure inductive circuit connected with $$\mathrm{A} . \mathrm{C}$$. source
R = impedance of pure resistive circuit connected with A.C. source.
$$\mathrm{Z}=$$ Impedance of the LCR series circuit $$\}$$
Given below are two statements:
Statement I : Maximum power is dissipated in a circuit containing an inductor, a capacitor and a resistor connected in series with an AC source, when resonance occurs
Statement II : Maximum power is dissipated in a circuit containing pure resistor due to zero phase difference between current and voltage.
In the light of the above statements, choose the correct answer from the options given below:
A capacitor of capacitance $$150.0 ~\mu \mathrm{F}$$ is connected to an alternating source of emf given by $$\mathrm{E}=36 \sin (120 \pi \mathrm{t}) \mathrm{V}$$. The maximum value of current in the circuit is approximately equal to :
Match List - I with List - II :
| List I | List II | ||
|---|---|---|---|
| A. | AC generator | I. | Presence of both L and C |
| B. | Transformer | II. | Electromagnetic Induction |
| C. | Resonance phenomenon to occur | III. | Quality factor |
| D. | Sharpness of resonance | IV. | Mutual Induction |
Choose the correct answer from the options given below :
If $$\mathrm{R}, \mathrm{X}_{\mathrm{L}}$$, and $$\mathrm{X}_{\mathrm{C}}$$ represent resistance, inductive reactance and capacitive reactance. Then which of the following is dimensionless :

In a series LR circuit with $$\mathrm{X_L=R}$$, power factor P1. If a capacitor of capacitance C with $$\mathrm{X_C=X_L}$$ is added to the circuit the power factor becomes P2. The ratio of P1 to P2 will be :
For the given figures, choose the correct options :

In an LC oscillator, if values of inductance and capacitance become twice and eight times, respectively, then the resonant frequency of oscillator becomes $$x$$ times its initial resonant frequency $$\omega_0$$. The value of $$x$$ is :
A circuit element $$\mathrm{X}$$ when connected to an a.c. supply of peak voltage $$100 \mathrm{~V}$$ gives a peak current of $$5 \mathrm{~A}$$ which is in phase with the voltage. A second element $$\mathrm{Y}$$ when connected to the same a.c. supply also gives the same value of peak current which lags behind the voltage by $$\frac{\pi}{2}$$. If $$\mathrm{X}$$ and $$\mathrm{Y}$$ are connected in series to the same supply, what will be the rms value of the current in ampere?
An alternating emf $$\mathrm{E}=440 \sin 100 \pi \mathrm{t}$$ is applied to a circuit containing an inductance of $$\frac{\sqrt{2}}{\pi} \mathrm{H}$$. If an a.c. ammeter is connected in the circuit, its reading will be :
A coil of inductance 1 H and resistance $$100 \,\Omega$$ is connected to a battery of 6 V. Determine approximately :
(a) The time elapsed before the current acquires half of its steady - state value.
(b) The energy stored in the magnetic field associated with the coil at an instant 15 ms after the circuit is switched on. (Given $$\ln 2=0.693, \mathrm{e}^{-3 / 2}=0.25$$)
A transformer operating at primary voltage $$8 \,\mathrm{kV}$$ and secondary voltage $$160 \mathrm{~V}$$ serves a load of $$80 \mathrm{~kW}$$. Assuming the transformer to be ideal with purely resistive load and working on unity power factor, the loads in the primary and secondary circuit would be
The equation of current in a purely inductive circuit is $$5 \sin \left(49\, \pi t-30^{\circ}\right)$$. If the inductance is $$30 \,\mathrm{mH}$$ then the equation for the voltage across the inductor, will be :
$$\left\{\right.$$ Let $$\left.\pi=\frac{22}{7}\right\}$$
A series LCR circuit has $$\mathrm{L}=0.01\, \mathrm{H}, \mathrm{R}=10\, \Omega$$ and $$\mathrm{C}=1 \mu \mathrm{F}$$ and it is connected to ac voltage of amplitude $$\left(\mathrm{V}_{\mathrm{m}}\right) 50 \mathrm{~V}$$. At frequency $$60 \%$$ lower than resonant frequency, the amplitude of current will be approximately :
A direct current of $$4 \mathrm{~A}$$ and an alternating current of peak value $$4 \mathrm{~A}$$ flow through resistance of $$3\, \Omega$$ and $$2\,\Omega$$ respectively. The ratio of heat produced in the two resistances in same interval of time will be :
In a series $$L R$$ circuit $$X_{L}=R$$ and power factor of the circuit is $$P_{1}$$. When capacitor with capacitance $$C$$ such that $$X_{L}=X_{C}$$ is put in series, the power factor becomes $$P_{2}$$. The ratio $$\frac{P_{1}}{P_{2}}$$ is:
When you walk through a metal detector carrying a metal object in your pocket, it raises an alarm. This phenomenon works on :
To increase the resonant frequency in series LCR circuit,
In series RLC resonator, if the self inductance and capacitance become double, the new resonant frequency (f2) and new quality factor (Q2) will be :
(f1 = original resonant frequency, Q1 = original quality factor)
For a series LCR circuit, I vs $$\omega$$ curve is shown :
(a) To the left of $$\omega$$r, the circuit is mainly capacitive.
(b) To the left of $$\omega$$r, the circuit is mainly inductive.
(c) At $$\omega$$r, impedance of the circuit is equal to the resistance of the circuit.
(d) At $$\omega$$r, impedance of the circuit is 0.

Choose the most appropriate answer from the options given below :
If L, C and R are the self inductance, capacitance and resistance respectively, which of the following does not have the dimension of time?
The current flowing through an ac circuit is given by
I = 5 sin(120$$\pi$$t)A
How long will the current take to reach the peak value starting from zero?
A sinusoidal voltage V(t) = 210 sin 3000 t volt is applied to a series LCR circuit in which L = 10 mH, C = 25 $$\mu$$F and R = 100 $$\Omega$$. The phase difference ($$\Phi $$) between the applied voltage and resultant current will be :
Match List-I with List-II.
| List - I | List -II | ||
|---|---|---|---|
| (A) | AC generator | (I) | Detects the presence of current in the circuit |
| (B) | Galvanometer | (II) | Converts mechanical energy into electrical energy |
| (C) | Transformer | (III) | Works on the principle of resonance in AC circuit |
| (D) | Metal detector | (IV) | Changes an alternating voltage for smaller or greater value |
Choose the correct answer from the options given below :
If wattless current flows in the AC circuit, then the circuit is :
Given below are two statements :
Statement I : The reactance of an ac circuit is zero. It is possible that the circuit contains a capacitor and an inductor.
Statement II : In ac circuit, the average power delivered by the source never becomes zero.
In the light of the above statements, choose the correct answer from the options given below.
A resistance of 40 $$\Omega$$ is connected to a source of alternating current rated 220 V, 50 Hz. Find the time taken by the current to change from its maximum value to the rms value :
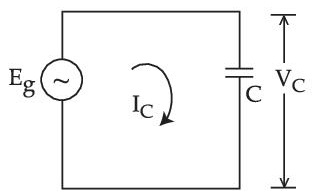
| List - I | List - II | ||
|---|---|---|---|
| (a) | $$\omega L > {1 \over {\omega C}}$$ | (i) | Current is in phase with emf |
| (b) | $$\omega L = {1 \over {\omega C}}$$ | (ii) | Current lags behind the applied emf |
| (c) | $$\omega L < {1 \over {\omega C}}$$ | (iii) | Maximum current occurs |
| (d) | Resonant frequency | (iv) | Current leads the emf |
Choose the correct answer from the options given below
| List - I | List - II | ||
|---|---|---|---|
| (a) | Phase difference between current and voltage in a purely resistive AC circuit | (i) | $${\pi \over 2}$$; current leads voltage |
| (b) | Phase difference between current and voltage in a pure inductive AC circuit | (ii) | zero |
| (c) | Phase difference between current and voltage in a pure capacitive AC circuit | (iii) | $${\pi \over 2}$$; current lags voltage |
| (d) | Phase difference between current and voltage in an LCR series circuit | (iv) | $${\tan ^{ - 1}}\left( {{{{X_C} - {X_L}} \over R}} \right)$$ |
Choose the most appropriate answer from the options given below :
| List I | List II | ||
|---|---|---|---|
| (a) | Rectifier | (i) | Used either for stepping up or stepping down the a.c. voltage |
| (b) | Stabilizer | (ii) | Used to convert a.c. voltage into d.c. voltage |
| (c) | Transformer | (iii) | Used to remove any ripple in the rectified output voltage |
| (d) | Filter | (iv) | Used for constant output voltage even when the input voltage or load current change |
Choose the correct answer from the options given below :
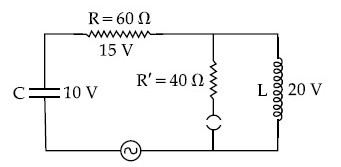
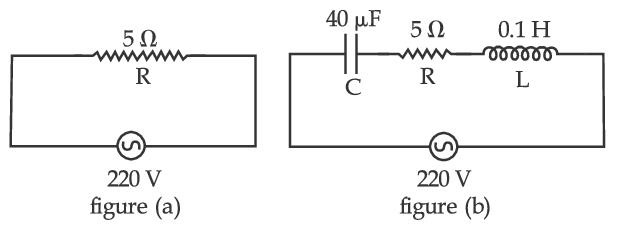
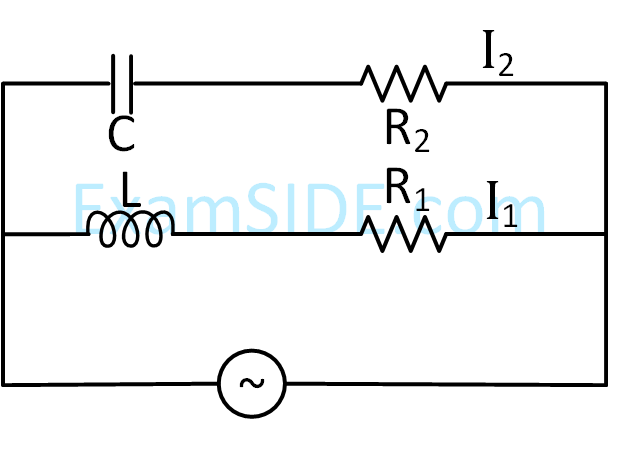
capacitance C = 100 $$\mu $$F. If a voltage
V(t) = 10sin(314t) is applied to the circuit, the
current in the circuit is given as :
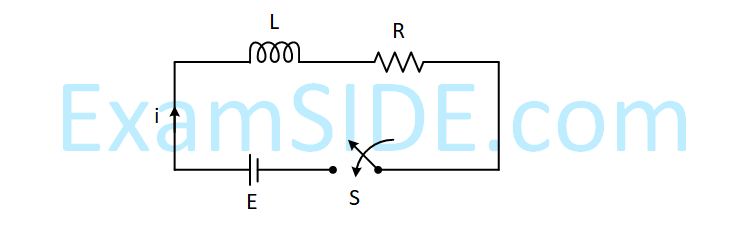
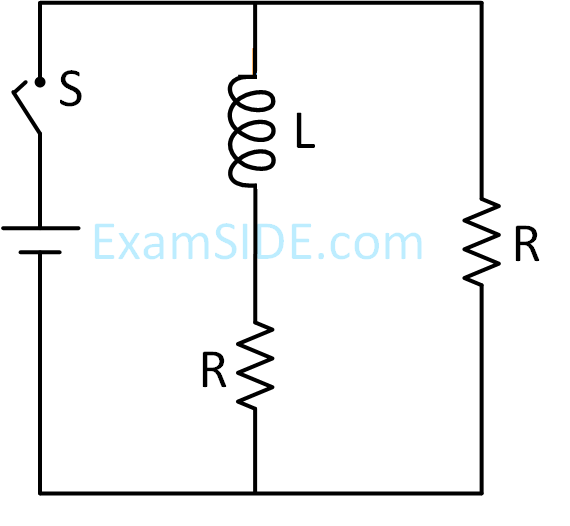
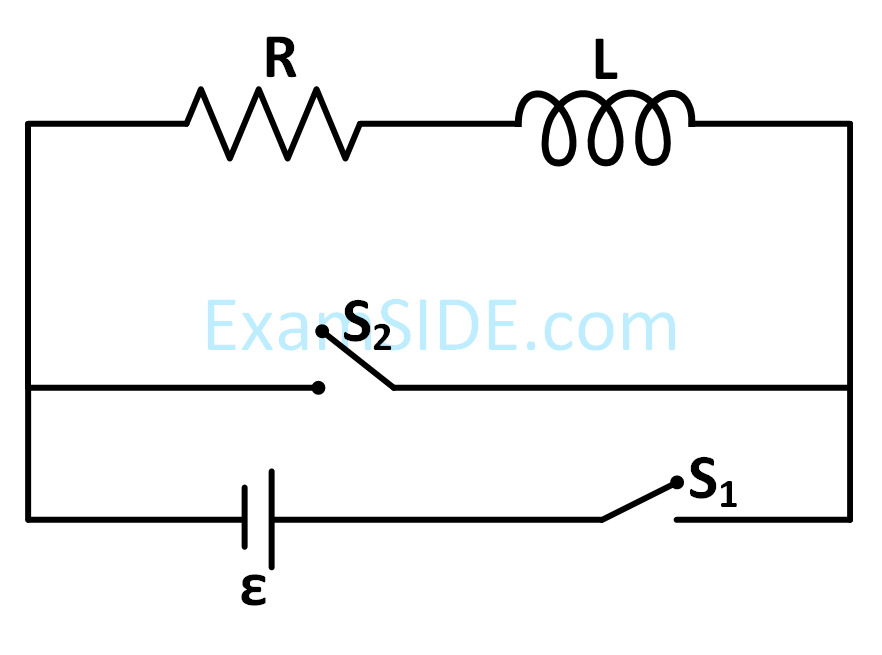
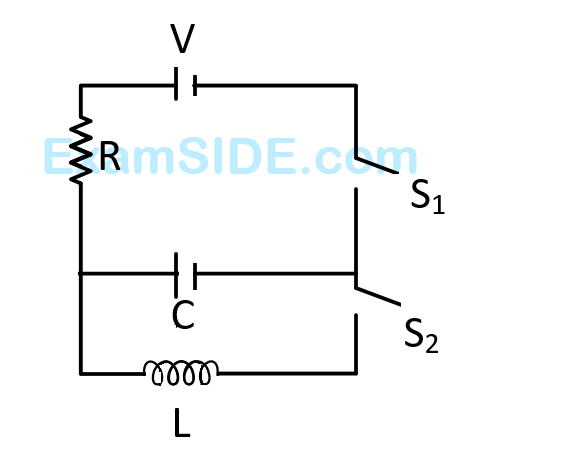
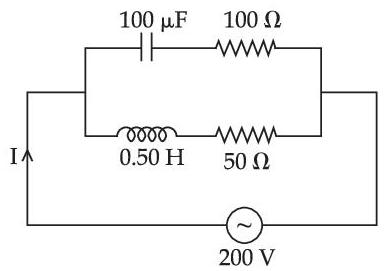
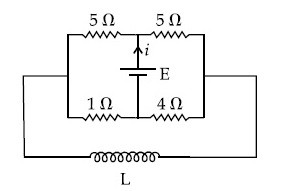
the switch S1 is closed at time t = 0 and the switch S2 is kept open. At some later time(t0), the switch S1 is opened and S2 is closed. The behavior of the current I as a function of time 't' is given by :
e = 100 sin 30 t
i = 20 sin $$\left( {30t - {\pi \over 4}} \right)$$
In one cycle of a.c., the average power consumed by the circuit and the wattless current are, respectively
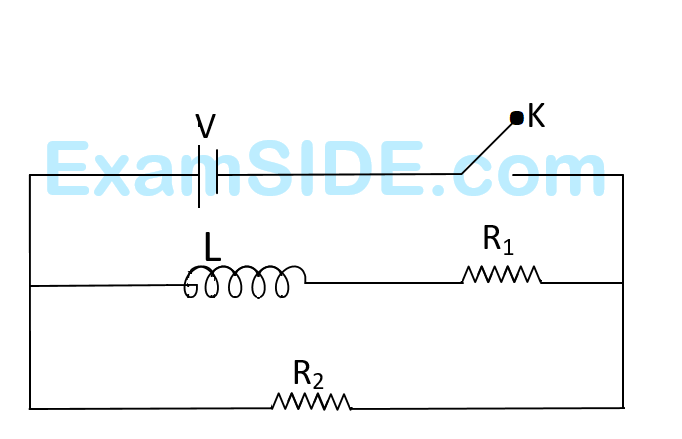
V(t) = V0 sin$$\Omega $$t. After very large time, current I(t) behaves as
(t0 >> $${L \over R}$$) :
An $$LCR$$ circuit is equivalent to a damped pendulum. In an $$LCR$$ circuit the capacitor is charged to $${Q_0}$$ and then connected to the $$L$$ and $$R$$ as shown below :

If a student plots graphs of the square of maximum charge $$\left( {Q_{Max}^2} \right)$$ on the capacitor with time$$(t)$$ for two different values $${L_1}$$ and $${L_2}$$ $$\left( {{L_1} > {L_2}} \right)$$ of $$L$$ then which of the following represents this graph correctly ?
$$\left( {plots\,\,are\,\,schematic\,\,and\,\,niot\,\,drawn\,\,to\,\,scale} \right)$$