Atoms and Nuclei · Physics · JEE Main
MCQ (Single Correct Answer)
For a nucleus of mass number A and radius R, the mass density of nucleus can be represented as
Given below are two statements: one is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A): The density of the copper $(^ {64}_{29} \text{Cu})$ nucleus is greater than that of the carbon $(^ {12}_{6} \text{C})$ nucleus.
Reason (R): The nucleus of mass number A has a radius proportional to $ A^{1/3} $.
In the light of the above statements, choose the most appropriate answer from the options given below:
In a hydrogen like ion, the energy difference between the $2^{\text {nd }}$ excitation energy state and ground is 108.8 eV . The atomic number of the ion is:
For a hydrogen atom, the ratio of the largest wavelength of Lyman series to that of the Balmer series is
A radioactive material $P$ first decays into $Q$ and then $Q$ decays to non-radioactive material $R$. Which of the following figure represents time dependent mass of $P, Q$ and $R$ ?
Given below are two statements :
Statement (I) : The dimensions of Planck's constant and angular momentum are same.
Statement (II) : In Bohr's model electron revolve around the nucleus only in those orbits for which angular momentum is integral multiple of Planck's constant.
In the light of the above statements, choose the most appropriate answer from the options given below :
Considering the Bohr model of hydrogen like atoms, the ratio of the radius of $5^{\text {th }}$ orbit of the electron in $\mathrm{Li}^{2+}$ and $\mathrm{He}^{+}$is
Given below are two statements: one is labelled as $\mathbf{A s s e r t i o n} \mathbf{A}$ and the other is labelled as Reason $\mathbf{R}$
Assertion A : The Bohr model is applicable to hydrogen and hydrogen-like atoms only.
Reason $\mathbf{R}$ : The formulation of Bohr model does not include repulsive force between electrons.
In the light of the above statements, choose the correct answer from the options given below
$$ \text { Match the LIST-I with LIST-II } $$
| List - I |
List - II |
||
|---|---|---|---|
| A. | $$ { }_0^1 \mathrm{n}+{ }_{92}^{235} \mathrm{U} \rightarrow{ }_{54}^{140} \mathrm{Xe}+{ }_{38}^{94} \mathrm{Sr}+2{ }_0^1 \mathrm{n} $$ |
I. | $$ \text { Chemical reaction } $$ |
| B. | $$ 2 \mathrm{H}_2+\mathrm{O}_2 \rightarrow 2 \mathrm{H}_2 \mathrm{O} $$ |
II. | $$ \text { Fusion with +ve } \mathrm{Q} \text { value } $$ |
| C. | $$ { }_1^2 \mathrm{H}+{ }_1^2 \mathrm{H} \rightarrow{ }_2^3 \mathrm{He}+{ }_0^1 \mathrm{n} $$ |
III. | $$ \text { Fission } $$ |
| D. | $$ { }_1^1 \mathrm{H}+{ }_1^3 \mathrm{H} \rightarrow{ }_1^2 \mathrm{H}+{ }_1^2 \mathrm{H} $$ |
IV. | $$ \text { Fusion with -ve } Q \text { value } $$ |
Considering Bohr's atomic model for hydrogen atom :
(A) the energy of H atom in ground state is same as energy of $\mathrm{He}^{+}$ion in its first excited state.
(B) the energy of H atom in ground state is same as that for $\mathrm{Li}^{++}$ ion in its second excited state.
(C) the energy of H atom in its ground state is same as that of $\mathrm{He}^{+}$ion for its ground state.
(D) the energy of $\mathrm{He}^{+}$ion in its first excited state is same as that for $\mathrm{Li}^{++}$ion in its ground state.
Choose the correct answer from the options given below :
The number of spectral lines emitted by atomic hydrogen that is in the 4th energy level, is
The frequency of revolution of the electron in Bohr's orbit varies with n, the principal quantum number as:
Choose the correct nuclear process from the below options [ p : proton, n : neutron, $\mathrm{e}^{-}$: electron, $\mathrm{e}^{+}$: positron, $v:$ neutrino, $\bar{v}:$ antineutrino]
The energy E and momentum p of a moving body of mass m are related by some equation. Given that c represents the speed of light, identify the correct equation
Given below are two statements. One is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : The binding energy per nucleon is found to be practically independent of the atomic number A , for nuclei with mass numbers between 30 and 170 .
Reason (R) : Nuclear force is long range. In the light of the above statements, choose the correct answer from the options given below :
A radioactive nucleus $\mathrm{n}_2$ has 3 times the decay constant as compared to the decay constant of another radioactive nucleus $n_1$. If initial number of both nuclei are the same, what is the ratio of number of nuclei of $n_2$ to the number of nuclei of $n_1$, after one half-life of $n_1$ ?
A nucleus at rest disintegrates into two smaller nuclei with their masses in the ratio of $$2: 1$$. After disintegration they will move :
The energy released in the fusion of $$2 \mathrm{~kg}$$ of hydrogen deep in the sun is $$E_H$$ and the energy released in the fission of $$2 \mathrm{~kg}$$ of $${ }^{235} \mathrm{U}$$ is $$E_U$$. The ratio $$\frac{E_H}{E_U}$$ is approximately: (Consider the fusion reaction as $$4_1^1H+2 \mathrm{e}^{-} \rightarrow{ }_2^4 \mathrm{He}+2 v+6 \gamma+26.7 \mathrm{~MeV}$$, energy released in the fission reaction of $${ }^{235} \mathrm{U}$$ is $$200 \mathrm{~MeV}$$ per fission nucleus and $$\mathrm{N}_{\mathrm{A}}= 6.023 \times 10^{23})$$
A hydrogen atom in ground state is given an energy of $$10.2 \mathrm{~eV}$$. How many spectral lines will be emitted due to transition of electrons?
The energy equivalent of $$1 \mathrm{~g}$$ of substance is :
If $$M_0$$ is the mass of isotope $${ }_5^{12} B, M_p$$ and $$M_n$$ are the masses of proton and neutron, then nuclear binding energy of isotope is:
In a hypothetical fission reaction
$${ }_{92} X^{236} \rightarrow{ }_{56} \mathrm{Y}^{141}+{ }_{36} Z^{92}+3 R$$
The identity of emitted particles (R) is :
Binding energy of a certain nucleus is $$18 \times 10^8 \mathrm{~J}$$. How much is the difference between total mass of all the nucleons and nuclear mass of the given nucleus:
The longest wavelength associated with Paschen series is : (Given $$\mathrm{R}_{\mathrm{H}}=1.097 \times 10^7 \mathrm{SI}$$ unit)
The ratio of the shortest wavelength of Balmer series to the shortest wavelength of Lyman series for hydrogen atom is :
The angular momentum of an electron in a hydrogen atom is proportional to : (Where $$\mathrm{r}$$ is the radius of orbit of electron)
An electron rotates in a circle around a nucleus having positive charge $$\mathrm{Ze}$$. Correct relation between total energy (E) of electron to its potential energy (U) is :
According to Bohr's theory, the moment of momentum of an electron revolving in $$4^{\text {th }}$$ orbit of hydrogen atom is:
Which of the following nuclear fragments corresponding to nuclear fission between neutron $$\left({ }_0^1 \mathrm{n}\right)$$ and uranium isotope $$\left({ }_{92}^{235} \mathrm{U}\right)$$ is correct :
(A) The angular momentum of an electron in $n^{\text {th }}$ orbit is an integral multiple of $\hbar$.
(B) Nuclear forces do not obey inverse square law.
(C) Nuclear forces are spin dependent.
(D) Nuclear forces are central and charge independent.
(E) Stability of nucleus is inversely proportional to the value of packing fraction.
Choose the correct answer from the options given below :
The mass number of nucleus having radius equal to half of the radius of nucleus with mass number 192 is :
If the wavelength of the first member of Lyman series of hydrogen is $$\lambda$$. The wavelength of the second member will be
An electron revolving in $$n^{\text {th }}$$ Bohr orbit has magnetic moment $$\mu_n$$. If $$\mu_n \propto n^x$$, the value of $$x$$ is
In a nuclear fission reaction of an isotope of mass $$M$$, three similar daughter nuclei of same mass are formed. The speed of a daughter nuclei in terms of mass defect $$\Delta M$$ will be :
The ratio of the magnitude of the kinetic energy to the potential energy of an electron in the 5th excited state of a hydrogen atom is :
Given below are two statements:
Statement I : Most of the mass of the atom and all its positive charge are concentrated in a tiny nucleus and the electrons revolve around it, is Rutherford's model.
Statement II : An atom is a spherical cloud of positive charges with electrons embedded in it, is a special case of Rutherford's model.
In the light of the above statements, choose the most appropriate from the options given below
The explosive in a Hydrogen bomb is a mixture of $${ }_1 \mathrm{H}^2,{ }_1 \mathrm{H}^3$$ and $${ }_3 \mathrm{Li}^6$$ in some condensed form. The chain reaction is given by
$$\begin{aligned} & { }_3 \mathrm{Li}^6+{ }_0 \mathrm{n}^1 \rightarrow{ }_2 \mathrm{He}^4+{ }_1 \mathrm{H}^3 \\ & { }_1 \mathrm{H}^2+{ }_1 \mathrm{H}^3 \rightarrow{ }_2 \mathrm{He}^4+{ }_0 \mathrm{n}^1 \end{aligned}$$
During the explosion the energy released is approximately
[Given ; $$\mathrm{M}(\mathrm{Li})=6.01690 \mathrm{~amu}, \mathrm{M}\left({ }_1 \mathrm{H}^2\right)=2.01471 \mathrm{~amu}, \mathrm{M}\left({ }_2 \mathrm{He}^4\right)=4.00388$$ $$\mathrm{amu}$$, and $$1 \mathrm{~amu}=931.5 \mathrm{~MeV}]$$
The atomic mass of $${ }_6 \mathrm{C}^{12}$$ is $$12.000000 \mathrm{~u}$$ and that of $${ }_6 \mathrm{C}^{13}$$ is $$13.003354 \mathrm{~u}$$. The required energy to remove a neutron from $${ }_6 \mathrm{C}^{13}$$, if mass of neutron is $$1.008665 \mathrm{~u}$$, will be :
The radius of third stationary orbit of electron for Bohr's atom is R. The radius of fourth stationary orbit will be:
Given below are two statements: one is labelled as Assertion $$\mathbf{A}$$ and the other is labelled as Reason $$\mathbf{R}$$
Assertion A : The binding energy per nucleon is practically independent of the atomic number for nuclei of mass number in the range 30 to 170 .
Reason R : Nuclear force is short ranged.
In the light of the above statements, choose the correct answer from the options given below
$$_{92}^{238}A \to _{90}^{234}B + _2^4D + Q$$
In the given nuclear reaction, the approximate amount of energy released will be:
[Given, mass of $${ }_{92}^{238} \mathrm{~A}=238.05079 \times 931.5 ~\mathrm{MeV} / \mathrm{c}^{2},$$
mass of $${ }_{90}^{234} B=234 \cdot 04363 \times 931 \cdot 5 ~\mathrm{MeV} / \mathrm{c}^{2},$$
mass of $$\left.{ }_{2}^{4} D=4 \cdot 00260 \times 931 \cdot 5 ~\mathrm{MeV} / \mathrm{c}^{2}\right]$$
A $$12.5 \mathrm{~eV}$$ electron beam is used to bombard gaseous hydrogen at room temperature. The number of spectral lines emitted will be:
The energy of $$\mathrm{He}^{+}$$ ion in its first excited state is, (The ground state energy for the Hydrogen atom is $$-13.6 ~\mathrm{eV})$$ :
Two radioactive elements A and B initially have same number of atoms. The half life of A is same as the average life of B. If $$\lambda_{A}$$ and $$\lambda_{B}$$ are decay constants of A and B respectively, then choose the correct relation from the given options.
The half life of a radioactive substance is T. The time taken, for disintegrating $$\frac{7}{8}$$th part of its original mass will be:
The angular momentum for the electron in Bohr's orbit is L. If the electron is assumed to revolve in second orbit of hydrogen atom, then the change in angular momentum will be
A radio active material is reduced to $$1 / 8$$ of its original amount in 3 days. If $$8 \times 10^{-3} \mathrm{~kg}$$ of the material is left after 5 days the initial amount of the material is
The waves emitted when a metal target is bombarded with high energy electrons are
For a nucleus $${ }_{\mathrm{A}}^{\mathrm{A}} \mathrm{X}$$ having mass number $$\mathrm{A}$$ and atomic number $$\mathrm{Z}$$
A. The surface energy per nucleon $$\left(b_{\mathrm{s}}\right)=-a_{1} A^{2 / 3}$$.
B. The Coulomb contribution to the binding energy $$\mathrm{b}_{\mathrm{c}}=-a_{2} \frac{Z(Z-1)}{A^{4 / 3}}$$
C. The volume energy $$\mathrm{b}_{\mathrm{v}}=a_{3} A$$
D. Decrease in the binding energy is proportional to surface area.
E. While estimating the surface energy, it is assumed that each nucleon interacts with 12 nucleons. ( $$a_{1}, a_{2}$$ and $$a_{3}$$ are constants)
Choose the most appropriate answer from the options given below:
A small particle of mass $$m$$ moves in such a way that its potential energy $$U=\frac{1}{2} m ~\omega^{2} r^{2}$$ where $$\omega$$ is constant and $$r$$ is the distance of the particle from origin. Assuming Bohr's quantization of momentum and circular orbit, the radius of $$n^{\text {th }}$$ orbit will be proportional to,
The energy levels of an hydrogen atom are shown below. The transition corresponding to emission of shortest wavelength is :

An electron of a hydrogen like atom, having $$Z=4$$, jumps from $$4^{\text {th }}$$ energy state to $$2^{\text {nd }}$$ energy state. The energy released in this process, will be :
(Given Rch = $$13.6~\mathrm{eV}$$)
Where R = Rydberg constant
c = Speed of light in vacuum
h = Planck's constant
The mass of proton, neutron and helium nucleus are respectively $$1.0073~u,1.0087~u$$ and $$4.0015~u$$. The binding energy of helium nucleus is :
A free neutron decays into a proton but a free proton does not decay into neutron. This is because
Assertion A: The nuclear density of nuclides ${ }_{5}^{10} \mathrm{~B},{ }_{3}^{6} \mathrm{Li},{ }_{26}^{56} \mathrm{Fe},{ }_{10}^{20} \mathrm{Ne}$ and ${ }_{83}^{209} \mathrm{Bi}$ can be arranged as $\rho_{\mathrm{Bi}}^{\mathrm{N}}>\rho_{\mathrm{Fe}}^{\mathrm{N}}>\rho_{\mathrm{Ne}}^{\mathrm{N}}>\rho_{\mathrm{B}}^{\mathrm{N}}>\rho_{\mathrm{Li}}^{\mathrm{N}}$
Reason R: The radius $R$ of nucleus is related to its mass number $A$ as $R=R_{0} A^{1 / 3}$, where $R_{0}$ is a constant.
In the light of the above statements, choose the correct answer from the options given below
Speed of an electron in Bohr's $$7^{\text {th }}$$ orbit for Hydrogen atom is $$3.6 \times 10^{6} \mathrm{~m} / \mathrm{s}$$. The corresponding speed of the electron in $$3^{\text {rd }}$$ orbit, in $$\mathrm{m} / \mathrm{s}$$ is :
Substance A has atomic mass number 16 and half life of 1 day. Another substance B has atomic mass number 32 and half life of $$\frac{1}{2}$$ day. If both A and B simultaneously start undergo radio activity at the same time with initial mass 320 g each, how many total atoms of A and B combined would be left after 2 days.
If a radioactive element having half-life of $$30 \mathrm{~min}$$ is undergoing beta decay, the fraction of radioactive element remains undecayed after $$90 \mathrm{~min}$$. will be
The energy levels of an atom is shown in figure.

Which one of these transitions will result in the emission of a photon of wavelength 124.1 nm?
Given (h = 6.62 $$\times$$ 10$$^{-34}$$ Js)
The ratio of the density of oxygen nucleus ($$_8^{16}O$$) and helium nucleus ($$_2^{4}\mathrm{He}$$) is
A photon is emitted in transition from n = 4 to n = 1 level in hydrogen atom. The corresponding wavelength for this transition is (given, h = 4 $$\times$$ 10$$^{-15}$$ eVs) :
Consider the following radioactive decay process
$$_{84}^{218}A\buildrel \alpha \over \longrightarrow {A_1}\buildrel {{\beta ^ - }} \over \longrightarrow {A_2}\buildrel \gamma \over \longrightarrow {A_3}\buildrel \alpha \over \longrightarrow {A_4}\buildrel {{\beta ^ + }} \over \longrightarrow {A_5}\buildrel \gamma \over \longrightarrow {A_6}$$
The mass number and the atomic number of A$$_6$$ are given by :
Read the following statements :
(A) Volume of the nucleus is directly proportional to the mass number.
(B) Volume of the nucleus is independent of mass number.
(C) Density of the nucleus is directly proportional to the mass number.
(D) Density of the nucleus is directly proportional to the cube root of the mass number.
(E) Density of the nucleus is independent of the mass number.
Choose the correct option from the following options.
Find the ratio of energies of photons produced due to transition of an electron of hydrogen atom from its (i) second permitted energy level to the first level, and (ii) the highest permitted energy level to the first permitted level.
A radioactive sample decays $$\frac{7}{8}$$ times its original quantity in 15 minutes. The half-life of the sample is
The half life period of a radioactive substance is 60 days. The time taken for $$\frac{7}{8}$$th of its original mass to disintegrate will be :
The activity of a radioactive material is $$6.4 \times 10^{-4}$$ curie. Its half life is 5 days. The activity will become $$5 \times 10^{-6}$$ curie after :
What is the half-life period of a radioactive material if its activity drops to $$1 / 16^{\text {th }}$$ of its initial value in 30 years?
A nucleus of mass $$M$$ at rest splits into two parts having masses $$\frac{M^{\prime}}{3}$$ and $${{2M'} \over 3}(M' < M)$$. The ratio of de Broglie wavelength of two parts will be :
Mass numbers of two nuclei are in the ratio of $$4: 3$$. Their nuclear densities will be in the ratio of
The disintegration rate of a certain radioactive sample at any instant is 4250 disintegrations per minute. 10 minutes later, the rate becomes 2250 disintegrations per minute. The approximate decay constant is :
$$\left(\right.$$Take $$\left.\log _{10} 1.88=0.274\right)$$
Hydrogen atom from excited state comes to the ground state by emitting a photon of wavelength $$\lambda$$. The value of principal quantum number '$$n$$' of the excited state will be : ($$\mathrm{R}:$$ Rydberg constant)
The momentum of an electron revolving in $$\mathrm{n}^{\text {th }}$$ orbit is given by :
(Symbols have their usual meanings)
The magnetic moment of an electron (e) revolving in an orbit around nucleus with an orbital angular momentum is given by :
A hydrogen atom in ground state absorbs 12.09 eV of energy. The orbital angular momentum of the electron is increased by :
In the following nuclear reaction,
$$D\buildrel \alpha \over \longrightarrow {D_1}\buildrel {{\beta ^ - }} \over \longrightarrow {D_2}\buildrel \alpha \over \longrightarrow {D_3}\buildrel \gamma \over \longrightarrow {D_4}$$
Mass number of D is 182 and atomic number is 74. Mass number and atomic number of D4 respectively will be _________.
The activity of a radioactive material is 2.56 $$\times$$ 10$$-$$3 Ci. If the half life of the material is 5 days, after how many days the activity will become 2 $$\times$$ 10$$-$$5 Ci ?
Following statements related to radioactivity are given below :
(A) Radioactivity is a random and spontaneous process and is dependent on physical and chemical conditions.
(B) The number of un-decayed nuclei in the radioactive sample decays exponentially with time.
(C) Slope of the graph of loge (no. of undecayed nuclei) Vs. time represents the reciprocal of mean life time ($$\tau$$).
(D) Product of decay constant ($$\lambda$$) and half-life time (T1/2) is not constant.
Choose the most appropriate answer from the options given below :
The Q-value of a nuclear reaction and kinetic energy of the projectile particle, Kp are related as :
Given below are two statements :
Statement I : In hydrogen atom, the frequency of radiation emitted when an electron jumps from lower energy orbit (E1) to higher energy orbit (E2), is given as hf = E1 $$-$$ E2
Statement II : The jumping of electron from higher energy orbit (E2) to lower energy orbit (E1) is associated with frequency of radiation given as f = (E2 $$-$$ E1)/h
This condition is Bohr's frequency condition.
In the light of the above statements, choose the correct answer from the options given below :
A hydrogen atom in its ground state absorbs 10.2 eV of energy. The angular momentum of electron of the hydrogen atom will increase by the value of :
(Given, Planck's constant = 6.6 $$\times$$ 10$$-$$34 Js).
A radioactive nucleus can decay by two different processes. Half-life for the first process is 3.0 hours while it is 4.5 hours for the second process. The effective half-life of the nucleus will be:
How many alpha and beta particles are emitted when Uranium 92U238 decays to lead 82Pb206 ?
Which of the following figure represents the variation of $${l_n}\left( {{R \over {{R_0}}}} \right)$$ with $${l_n}A$$ (if R = radius of a nucleus and A = its mass number)
The ratio for the speed of the electron in the 3rd orbit of He+ to the speed of the electron in the 3rd orbit of hydrogen atom will be :
In Bohr's atomic model of hydrogen, let K, P and E are the kinetic energy, potential energy and total energy of the electron respectively. Choose the correct option when the electron undergoes transitions to a higher level :
Choose the correct option from the following options given below :
Nucleus A is having mass number 220 and its binding energy per nucleon is 5.6 MeV. It splits in two fragments 'B' and 'C' of mass numbers 105 and 115. The binding energy of nucleons in 'B' and 'C' is 6.4 MeV per nucleon. The energy Q released per fission will be :
(Assume that at t = 0, there are no B atoms in the sample)
[NA (0) = No. of A atoms at t = 0
NB (0) = No. of B atoms at t = 0]
A. Atoms of each element emit characteristics spectrum.
B. According to Bohr's Postulate, an electron in a hydrogen atom, revolves in a certain stationary orbit.
C. The density of nuclear matter depends on the size of the nucleus.
D. A free neutron is stable but a free proton decay is possible.
E. Radioactivity is an indication of the instability of nuclei.
Choose the correct answer from the options given below :
[$$\lambda$$ is the radioactive decay constant]
(where $$\lambda$$ is the decay constant)
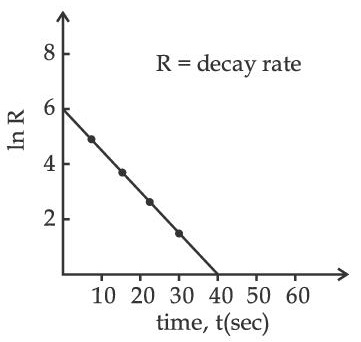
[Take 'c' as the speed of electromagnetic wave]
The transitions A, B and C respectively represent :

mp = 1.0072 u, mn = 1.0087 u, me = 0.000548 u,
$${m_{\overline v }}$$ = 0, md = 2.0141 u, where p $$ \equiv $$ proton, n $$ \equiv $$ neutron,
e $$ \equiv $$ electron, $$\overline v $$ $$ \equiv $$ antineutrino and d $$ \equiv $$ deuteron. Which of the following process is allowed by momentum and energy conservation?
Mass of $${}_2^4He$$ = 4.0026u
and Mass of $${}_1^1H$$ = 1.0079u.
When 20 g of $${}_3^7Li$$ is converted into $${}_2^4He$$ by proton capture, the energy liberated, (in kWh), is :
[Mass of nucleon = 1 GeV/c2]
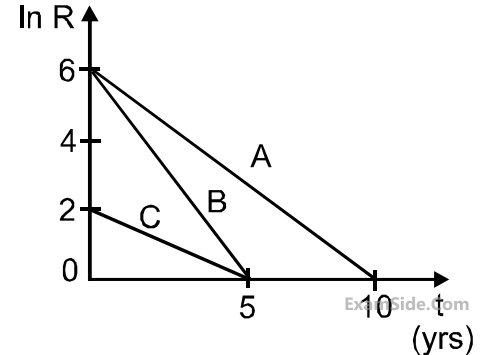
$${T_{{1 \over 2}}}\left( A \right)$$ : $${T_{{1 \over 2}}}\left( B \right)$$ : $${T_{{1 \over 2}}}\left( C \right)$$ are in the ratio :
R = (1.3 $$ \times $$ 10–15)A1/3 m.
It follows that the mass density of a nucleus is of the order of :
(Mprot. $$ \cong $$ Mneut $$ \simeq $$ 1.67 $$ \times $$ 10–27 kg)
$$\theta $$ : Scattering angle
Y : Number of scattered $$\alpha $$-particles detected (Plots are schematic and not to scale)
(Given : H = 6.63 × 10–34 Js; c = 3 × 108 ms –1)
Ne20 $$ \to $$ 2He4 + C12
Given that the binding energy/ nucleon of Ne20, He4 and C12 are, respectively, 8.03 MeV, 7.07 MeV and 7.86 MeV, identify the correct statement -
(A) Radis of the muonic orbit is 200 times smaller than that of the electron.
(B) The speed of the $$\mu $$$$-$$ in the nth orbit is $${1 \over {200}}$$ times that of the electron in the nth orbit.
(C) The ionization energy of muonic atom is 200 timesmore than of an hydroen atom.
(D) The momentum of the muon in the nth orbit is 200 times more than that of the electron.
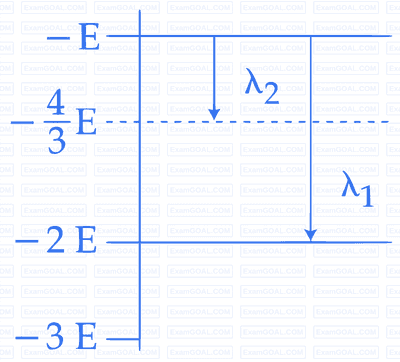
The binding energy per nucleon for the parent nucleus is $${E_1}$$ and that for the daughter nuclei is $${E_2}.$$ Then
The speed of daughter nuclei is
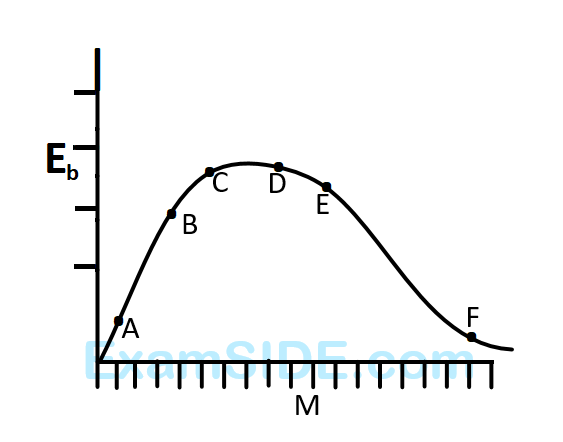
The above is a plot of binding energy per nucleon $${E_b},$$ against the nuclear mass $$M;A,B,C,D,E,F$$ correspond to different nuclei. Consider four reactions :
$$\eqalign{
& \left( i \right)\,\,\,\,\,\,\,\,\,\,A + B \to C + \varepsilon \,\,\,\,\,\,\,\,\,\,\left( {ii} \right)\,\,\,\,\,\,\,\,\,\,C \to A + B + \varepsilon \,\,\,\,\,\,\,\,\,\, \cr
& \left( {iii} \right)\,\,\,\,\,\,D + E \to F + \varepsilon \,\,\,\,\,\,\,\,\,\,\left( {iv} \right)\,\,\,\,\,\,\,\,\,F \to D + E + \varepsilon ,\,\,\,\,\,\,\,\,\,\, \cr} $$
where $$\varepsilon $$ is the energy released? In which reactions is $$\varepsilon $$ positive?
Statement- 1:
Energy is released when heavy nuclei undergo fission or light nuclei undergo fusion and
Statement- 2:
For heavy nuclei, binding energy per nucleon increases with increasing $$Z$$ while for light nuclei it decreases with increasing $$Z.$$
Then which of the following is true?
energy of proton must be
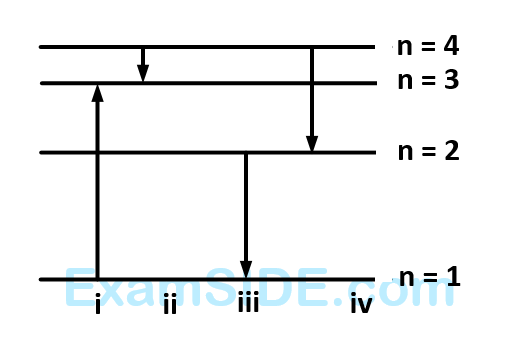
Then $$Z$$ of the resulting nucleus is
given that the repulsive potential energy between the two nuclei is $$ \sim 7.7 \times {10^{ - 14}}J$$, the temperature at which the gases must be heated to initiate the reaction is nearly
[ Boltzmann's Constant $$k = 1.38 \times {10^{ - 23}}\,J/K$$ ]
$$\eqalign{ & \left( i \right)\,\,\,\,\,\,\,electrons\,\,\,\,\,\,\,\,\,\,\,\,\left( {ii} \right)\,\,\,\,\,\,\,protons \cr & \left( {iii} \right)\,\,\,H{e^{2 + }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {iv} \right)\,\,\,\,\,\,\,neutrons \cr} $$
The emission at instant can be
Numerical
An electron in the hydrogen atom initially in the fourth excited state makes a transition to $\mathrm{n}^{\text {th }}$ energy state by emitting a photon of energy 2.86 eV . The integer value of n will be__________.
A star has $$100 \%$$ helium composition. It starts to convert three $${ }^4 \mathrm{He}$$ into one $${ }^{12} \mathrm{C}$$ via triple alpha process as $${ }^4 \mathrm{He}+{ }^4 \mathrm{He}+{ }^4 \mathrm{He} \rightarrow{ }^{12} \mathrm{C}+\mathrm{Q}$$. The mass of the star is $$2.0 \times 10^{32} \mathrm{~kg}$$ and it generates energy at the rate of $$5.808 \times 10^{30} \mathrm{~W}$$. The rate of converting these $${ }^4 \mathrm{He}$$ to $${ }^{12} \mathrm{C}$$ is $$\mathrm{n} \times 10^{42} \mathrm{~s}^{-1}$$, where $$\mathrm{n}$$ is _________. [ Take, mass of $${ }^4 \mathrm{He}=4.0026 \mathrm{u}$$, mass of $${ }^{12} \mathrm{C}=12 \mathrm{u}$$]
In an alpha particle scattering experiment distance of closest approach for the $$\alpha$$ particle is $$4.5 \times 10^{-14} \mathrm{~m}$$. If target nucleus has atomic number 80 , then maximum velocity of $$\alpha$$-particle is __________ $$\times 10^5 \mathrm{~m} / \mathrm{s}$$ approximately.
($$\frac{1}{4 \pi \epsilon_0}=9 \times 10^9 \mathrm{SI}$$ unit, mass of $$\alpha$$ particle $$=6.72 \times 10^{-27} \mathrm{~kg}$$)
Radius of a certain orbit of hydrogen atom is 8.48 $$\mathop A\limits^o$$. If energy of electron in this orbit is $$E / x$$. then $$x=$$ ________ (Given $$\mathrm{a}_0=0.529$$ $$\mathop A\limits^o$$, $$E=$$ energy of electron in ground state).
The shortest wavelength of the spectral lines in the Lyman series of hydrogen spectrum is $$915\mathop A\limits^o$$. The longest wavelength of spectral lines in the Balmer series will be _______ $$\mathop A\limits^o$$.
If three helium nuclei combine to form a carbon nucleus then the energy released in this reaction is ________ $$\times 10^{-2} \mathrm{~MeV}$$. (Given $$1 \mathrm{u}=931 \mathrm{~MeV} / \mathrm{c}^2$$, atomic mass of helium $$=4.002603 \mathrm{u}$$)
The disintegration energy $$Q$$ for the nuclear fission of $${ }^{235} \mathrm{U} \rightarrow{ }^{140} \mathrm{Ce}+{ }^{94} \mathrm{Zr}+n$$ is _______ $$\mathrm{MeV}$$.
Given atomic masses of $${ }^{235} \mathrm{U}: 235.0439 u ;{ }^{140} \mathrm{Ce}: 139.9054 u, { }^{94} \mathrm{Zr}: 93.9063 u ; n: 1.0086 u$$, Value of $$c^2=931 \mathrm{~MeV} / \mathrm{u}$$.
A hydrogen atom changes its state from $$n=3$$ to $$n=2$$. Due to recoil, the percentage change in the wave length of emitted light is approximately $$1 \times 10^{-n}$$. The value of $$n$$ is _______.
[Given Rhc $$=13.6 \mathrm{~eV}, \mathrm{hc}=1242 \mathrm{~eV} \mathrm{~nm}, \mathrm{h}=6.6 \times 10^{-34} \mathrm{~J} \mathrm{~s}$$ mass of the hydrogenatom $$=1.6 \times 10^{-27} \mathrm{~kg}$$]
A nucleus has mass number $$A_1$$ and volume $$V_1$$. Another nucleus has mass number $$A_2$$ and Volume $$V_2$$. If relation between mass number is $$A_2=4 A_1$$, then $$\frac{V_2}{V_1}=$$ __________.
The mass defect in a particular reaction is $$0.4 \mathrm{~g}$$. The amount of energy liberated is $$n \times 10^7 \mathrm{~kWh}$$, where $$n=$$ __________. (speed of light $$\left.=3 \times 10^8 \mathrm{~m} / \mathrm{s}\right)$$
A electron of hydrogen atom on an excited state is having energy $$\mathrm{E}_{\mathrm{n}}=-0.85 \mathrm{~eV}$$. The maximum number of allowed transitions to lower energy level is _________.
Hydrogen atom is bombarded with electrons accelerated through a potential difference of $$\mathrm{V}$$, which causes excitation of hydrogen atoms. If the experiment is being performed at $$\mathrm{T}=0 \mathrm{~K}$$, the minimum potential difference needed to observe any Balmer series lines in the emission spectra will be $$\frac{\alpha}{10} \mathrm{~V}$$, where $$\alpha=$$ __________.
When a hydrogen atom going from $$n=2$$ to $$n=1$$ emits a photon, its recoil speed is $$\frac{x}{5} \mathrm{~m} / \mathrm{s}$$. Where $$x=$$ ________. (Use, mass of hydrogen atom $$=1.6 \times 10^{-27} \mathrm{~kg}$$)
If Rydberg's constant is $$R$$, the longest wavelength of radiation in Paschen series will be $$\frac{\alpha}{7 R}$$, where $$\alpha=$$ ________.
In a nuclear fission process, a high mass nuclide $$(A \approx 236)$$ with binding energy $$7.6 \mathrm{~MeV} /$$ Nucleon dissociated into middle mass nuclides $$(\mathrm{A} \approx 118)$$, having binding energy of $$8.6 \mathrm{~MeV} / \mathrm{Nucleon}$$. The energy released in the process would be ______ $$\mathrm{MeV}$$.

The radius of $$2^{\text {nd }}$$ orbit of $$\mathrm{He}^{+}$$ of Bohr's model is $$r_{1}$$ and that of fourth orbit of $$\mathrm{Be}^{3+}$$ is represented as $$r_{2}$$. Now the ratio $$\frac{r_{2}}{r_{1}}$$ is $$x: 1$$. The value of $$x$$ is ___________.
A common example of alpha decay is $${ }_{92}^{238} \mathrm{U} \longrightarrow{ }_{90}^{234} \mathrm{Th}+{ }_{2} \mathrm{He}^{4}+\mathrm{Q}$$
Given :
$${ }_{92}^{238} \mathrm{U}=238.05060 ~\mathrm{u}$$,
$${ }_{90}^{234} \mathrm{Th}=234.04360 ~\mathrm{u}$$,
$${ }_{2}^{4} \mathrm{He}=4.00260 ~\mathrm{u}$$ and
$$1 \mathrm{u}=931.5 \frac{\mathrm{MeV}}{c^{2}}$$
The energy released $$(Q)$$ during the alpha decay of $${ }_{92}^{238} \mathrm{U}$$ is __________ MeV
A nucleus disintegrates into two nuclear parts, in such a way that ratio of their nuclear sizes is $$1: 2^{1 / 3}$$. Their respective speed have a ratio of $$n: 1$$. The value of $n$ is __________.
If 917 $$\mathop A\limits^o $$ be the lowest wavelength of Lyman series then the lowest wavelength of Balmer series will be ___________ $$\mathop A\limits^o $$.
The decay constant for a radioactive nuclide is 1.5 $$\times$$ 10$$^{-5}$$ s$$^{-1}$$. Atomic weight of the substance is 60 g mole$$^{-1}$$, ($$N_A=6\times10^{23}$$). The activity of 1.0 $$\mu$$g of the substance is ___________ $$\times$$ 10$$^{10}$$ Bq.
The ratio of wavelength of spectral lines $$\mathrm{H}_{\alpha}$$ and $$\mathrm{H}_{\beta}$$ in the Balmer series is $$\frac{x}{20}$$. The value of $$x$$ is _________.
A nucleus with mass number 242 and binding energy per nucleon as $$7.6~ \mathrm{MeV}$$ breaks into two fragment each with mass number 121. If each fragment nucleus has binding energy per nucleon as $$8.1 ~\mathrm{MeV}$$, the total gain in binding energy is _________ $$\mathrm{MeV}$$.
Experimentally it is found that $$12.8 ~\mathrm{eV}$$ energy is required to separate a hydrogen atom into a proton and an electron. So the orbital radius of the electron in a hydrogen atom is $$\frac{9}{x} \times 10^{-10} \mathrm{~m}$$. The value of the $$x$$ is __________.
$$\left(1 \mathrm{eV}=1.6 \times 10^{-19} \mathrm{~J}, \frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} \mathrm{Nm}^{2} / \mathrm{C}^{2}\right.$$ and electronic charge $$\left.=1.6 \times 10^{-19} \mathrm{C}\right)$$
The radius of fifth orbit of the $$\mathrm{Li}^{++}$$ is __________ $$\times 10^{-12} \mathrm{~m}$$.
Take: radius of hydrogen atom $$ = 0.51\,\mathop A\limits^o $$
Nucleus A having $$Z=17$$ and equal number of protons and neutrons has $$1.2 ~\mathrm{MeV}$$ binding energy per nucleon.
Another nucleus $$\mathrm{B}$$ of $$Z=12$$ has total 26 nucleons and $$1.8 ~\mathrm{MeV}$$ binding energy per nucleons.
The difference of binding energy of $$\mathrm{B}$$ and $$\mathrm{A}$$ will be _____________ $$\mathrm{MeV}$$.
A light of energy $$12.75 ~\mathrm{eV}$$ is incident on a hydrogen atom in its ground state. The atom absorbs the radiation and reaches to one of its excited states. The angular momentum of the atom in the excited state is $$\frac{x}{\pi} \times 10^{-17} ~\mathrm{eVs}$$. The value of $$x$$ is ___________ (use $$h=4.14 \times 10^{-15} ~\mathrm{eVs}, c=3 \times 10^{8} \mathrm{~ms}^{-1}$$ ).
For hydrogen atom, $$\lambda_{1}$$ and $$\lambda_{2}$$ are the wavelengths corresponding to the transitions 1 and 2 respectively as shown in figure. The ratio of $$\lambda_{1}$$ and $$\lambda_{2}$$ is $$\frac{x}{32}$$. The value of $$x$$ is __________.

A radioactive nucleus decays by two different process. The half life of the first process is 5 minutes and that of the second process is $30 \mathrm{~s}$. The effective half-life of the nucleus is calculated to be $\frac{\alpha}{11} \mathrm{~s}$. The value of $\alpha$ is __________.
A radioactive element $$_{92}^{242}$$X emits two $$\alpha$$-particles, one electron and two positrons. The product nucleus is represented by $$_{\mathrm{P}}^{234}$$Y. The value of P is __________.
A nucleus disintegrates into two smaller parts, which have their velocities in the ratio 3 : 2. The ratio of their nuclear sizes will be $${\left( {{x \over 3}} \right)^{{1 \over 3}}}$$. The value of '$$x$$' is :-
The wavelength of the radiation emitted is $$\lambda_0$$ when an electron jumps from the second excited state to the first excited state of hydrogen atom. If the electron jumps from the third excited state to the second orbit of the hydrogen atom, the wavelength of the radiation emitted will $$\frac{20}{x}\lambda_0$$. The value of $$x$$ is _____________.
The energy released per fission of nucleus of $$^{240}$$X is 200 MeV. The energy released if all the atoms in 120g of pure $$^{240}$$X undergo fission is ____________ $$\times$$ 10$$^{25}$$ MeV.
(Given $$\mathrm{N_A=6\times10^{23}}$$)
Assume that protons and neutrons have equal masses. Mass of a nucleon is $$1.6\times10^{-27}$$ kg and radius of nucleus is $$1.5\times10^{-15}~\mathrm{A^{1/3}}$$ m. The approximate ratio of the nuclear density and water density is $$n\times10^{13}$$. The value of $$n$$ is __________.
Two radioactive materials A and B have decay constants $$25 \lambda$$ and $$16 \lambda$$ respectively. If initially they have the same number of nuclei, then the ratio of the number of nuclei of B to that of A will be "e" after a time $$\frac{1}{a \lambda}$$. The value of a is _________.
A freshly prepared radioactive source of half life 2 hours 30 minutes emits radiation which is 64 times the permissible safe level. The minimum time, after which it would be possible to work safely with source, will be _________ hours.
Two lighter nuclei combine to form a comparatively heavier nucleus by the relation given below :
$${ }_{1}^{2} X+{ }_{1}^{2} X={ }_{2}^{4} Y$$
The binding energies per nucleon for $$\frac{2}{1} X$$ and $${ }_{2}^{4} Y$$ are $$1.1 \,\mathrm{MeV}$$ and $$7.6 \,\mathrm{MeV}$$ respectively. The energy released in this process is _______________ $$\mathrm{MeV}$$.
In the hydrogen spectrum, $$\lambda$$ be the wavelength of first transition line of Lyman series. The wavelength difference will be "a$$\lambda$$'' between the wavelength of $$3^{\text {rd }}$$ transition line of Paschen series and that of $$2^{\text {nd }}$$ transition line of Balmer series where $$\mathrm{a}=$$ ___________.
$${x \over {x + 4}}$$ is the ratio of energies of photons produced due to transition of an electron of hydrogen atom from its
(i) third permitted energy level to the second level and
(ii) the highest permitted energy level to the second permitted level.
The value of x will be ____________.
A hydrogen atom in its first excited state absorbs a photon of energy x $$\times$$ 10$$-$$2 eV and excited to a higher energy state where the potential energy of electron is $$-$$1.08 eV. The value of x is ______________.
The half life of a radioactive substance is 5 years. After x years a given sample of the radioactive substance gets reduced to 6.25% of its initial value. The value of x is ____________.
$$\sqrt {{d_1}} $$ and $$\sqrt {{d_2}} $$ are the impact parameters corresponding to scattering angles 60$$^\circ$$ and 90$$^\circ$$ respectively, when an $$\alpha$$ particle is approaching a gold nucleus. For d1 = x d2, the value of x will be ____________.
A beam of monochromatic light is used to excite the electron in Li+ + from the first orbit to the third orbit. The wavelength of monochromatic light is found to be x $$\times$$ 10$$-$$10 m. The value of x is ___________.
[Given hc = 1242 eV nm]
A sample contains 10$$-$$2 kg each of two substances A and B with half lives 4 s and 8 s respectively. The ratio of their atomic weights is 1 : 2. The ratio of the amounts of A and B after 16 s is $${x \over {100}}$$. The value of x is ___________.
[h = 4.14 $$\times$$ 10$$-$$15 eVs, c = 3 $$\times$$ 108 ms$$-$$1]
Mass of neutron = 1.00866 u
Mass of proton = 1.00726 u
Mass of Aluminium nucleus = 27.18846 u
(Assume 1 u corresponds to x J of energy)
(Round off to the nearest integer)
central potential field U(r) = U0r4. If Bohr's quantization conditions
are applied, radii of possible
orbitals rn vary with $${n^{{1 \over \alpha }}}$$, where $$\alpha$$ is ____________.
given $$\lambda$$1, $$\lambda$$2, $$\lambda$$3 considering the Bohr atomic model, the wave lengths of first and third spectral lines $$\left( \frac{\lambda_{1} }{\lambda_{3} } \right) $$ are related by a factor of approximately 'x' $$\times$$ 10$$-$$1.
The value of x, to the nearest integer, is _________.
$${N \over 4}$$. The value of N is :
(Given the mass of the hydrogen atom to be 1 GeV/c2) ______ .