Electromagnetic Waves · Physics · JEE Main
MCQ (Single Correct Answer)
| List - I | List - II | ||
|---|---|---|---|
| (I) | Doublet of sodium | (A) | Visible radiation |
| (II) | Wavelength corresponding to temperature associated with the isotropic radiation filling all space |
(B) | Microwave |
| (III | Wavelength emitted by atomic hydrogen in interstellar space |
(C) | Short radiowave |
| (IV) | Wavelength of radiation arising from two close energy levels in hydrogen |
(D) | X - rays |

The unit of $\sqrt{\frac{2I}{\varepsilon_0 c}}$ is :
(I = intensity of an electromagnetic wave, c = speed of light)
A plane electromagnetic wave propagates along the + x direction in free space. The components of the electric field, $\vec{E}$ and magnetic field, $\vec{B}$ vectors associated with the wave in Cartesian frame are
Given below are two statements: one is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : Electromagnetic waves carry energy but not momentum.
Reason (R) : Mass of a photon is zero.
In the light of the above statements, choose the most appropriate answer from the options given below :
The magnetic field of an E.M. wave is given by $\vec{B} = \left( \frac{\sqrt{3}}{2} \hat{i} + \frac{1}{2} \hat{j} \right) 30 \sin \left[ \omega \left( t - \frac{z}{c} \right) \right]$ (S.I. Units).
The corresponding electric field in S.I. units is:
Due to presence of an em-wave whose electric component is given by $E=100 \sin (\omega t-k x) \mathrm{NC}^{-1}$ a cylinder of length 200 cm holds certain amount of em-energy inside it. If another cylinder of same length but half diameter than previous one holds same amount of em-energy, the magnitude of the electric field of the corresponding em-wave should be modified as
Arrange the following in the ascending order of wavelength $(\lambda)$ :
(A) Microwaves $\left(\lambda_1\right)$
(B) Ultraviolet rays $\left(\lambda_2\right)$
(C) Infrared rays $\left(\lambda_3\right)$
(D) X-rays $\left(\lambda_4\right)$
Choose the most appropriate answer from the options given below :
A plane electromagnetic wave of frequency 20 MHz travels in free space along the $+x$ direction. At a particular point in space and time, the electric field vector of the wave is $\mathrm{E}_y=9.3 \mathrm{Vm}^{-1}$. Then, the magnetic field vector of the wave at that point is
The electric field of an electromagnetic wave in free space is $\overrightarrow{\mathrm{E}}=57 \cos \left[7.5 \times 10^6 \mathrm{t}-5 \times 10^{-3}(3 x+4 y)\right](4 \hat{i}-3 \hat{j}) N / C$. The associated magnetic field in Tesla is
The magnetic field in a plane electromagnetic wave is $$\mathrm{B}_{\mathrm{y}}=\left(3.5 \times 10^{-7}\right) \sin \left(1.5 \times 10^3 x+0.5 \times 10^{11} t\right) \mathrm{T}$$. The corresponding electric field will be :
A plane EM wave is propagating along $$x$$ direction. It has a wavelength of $$4 \mathrm{~mm}$$. If electric field is in $$y$$ direction with the maximum magnitude of $$60 \mathrm{~Vm}^{-1}$$, the equation for magnetic field is :
Average force exerted on a non-reflecting surface at normal incidence is $$2.4 \times 10^{-4} \mathrm{~N}$$. If $$360 \mathrm{~W} / \mathrm{cm}^2$$ is the light energy flux during span of 1 hour 30 minutes, Then the area of the surface is:
In the given electromagnetic wave $$\mathrm{E}_{\mathrm{y}}=600 \sin (\omega t-\mathrm{kx}) \mathrm{Vm}^{-1}$$, intensity of the associated light beam is (in $$\mathrm{W} / \mathrm{m}^2$$ : (Given $$\epsilon_0=9 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}$$ )
Electromagnetic waves travel in a medium with speed of $$1.5 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}$$. The relative permeability of the medium is 2.0. The relative permittivity will be:
Match List I with List II :
| LIST I EM-Wave |
LIST II Wavelength Range |
||
|---|---|---|---|
| A. | Infra-red | I. | $$<10^{-3}$$ nm |
| B. | Ultraviolet | II. | 400 nm to 1 nm |
| C. | X-rays | III. | 1 mm to 700 nm |
| D. | Gamma rays | IV. | 1 nm to $$10^{-3}$$ nm |
Choose the correct answer from the options given below :
Arrange the following in the ascending order of wavelength:
A. Gamma rays $$\left(\lambda_1\right)$$
B. $$x$$ - rays $$\left(\lambda_2\right)$$
C. Infrared waves $$\left(\lambda_3\right)$$
D. Microwaves $$\left(\lambda_4\right)$$
Choose the most appropriate answer from the options given below
The electric field in an electromagnetic wave is given by $$\overrightarrow{\mathrm{E}}=\hat{i} 40 \cos \omega(\mathrm{t}-z / \mathrm{c}) \mathrm{NC}^{-1}$$. The magnetic field induction of this wave is (in SI unit) :
Given below are two statements:
Statement I: Electromagnetic waves carry energy as they travel through space and this energy is equally shared by the electric and magnetic fields.
Statement II: When electromagnetic waves strike a surface, a pressure is exerted on the surface.
In the light of the above statements, choose the most appropriate answer from the options given below:
In a plane EM wave, the electric field oscillates sinusoidally at a frequency of $$5 \times 10^{10} \mathrm{~Hz}$$ and an amplitude of $$50 \mathrm{~Vm}^{-1}$$. The total average energy density of the electromagnetic field of the wave is : [Use $$\varepsilon_0=8.85 \times 10^{-12} \mathrm{C}^2 / \mathrm{Nm}^2$$ ]
The electric field of an electromagnetic wave in free space is represented as $$\overrightarrow{\mathrm{E}}=\mathrm{E}_0 \cos (\omega \mathrm{t}-\mathrm{kz}) \hat{i}$$. The corresponding magnetic induction vector will be :
A plane electromagnetic wave of frequency $$35 \mathrm{~MHz}$$ travels in free space along the $$X$$-direction. At a particular point (in space and time) $$\vec{E}=9.6 \hat{j} \mathrm{~V} / \mathrm{m}$$. The value of magnetic field at this point is :
An object is placed in a medium of refractive index 3 . An electromagnetic wave of intensity $$6 \times 10^8 \mathrm{~W} / \mathrm{m}^2$$ falls normally on the object and it is absorbed completely. The radiation pressure on the object would be (speed of light in free space $$=3 \times 10^8 \mathrm{~m} / \mathrm{s}$$ ) :
A plane electromagnetic wave propagating in $$\mathrm{x}$$-direction is described by
$$E_y=\left(200 \mathrm{Vm}^{-1}\right) \sin \left[1.5 \times 10^7 t-0.05 x\right] \text {; }$$
The intensity of the wave is :
(Use $$\epsilon_0=8.85 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}$$)
| List I | List II |
|---|---|
| (A) Microwave | (I) $400 \mathrm{~nm}$ to $1 \mathrm{~nm}$ |
| (B) Ultraviolet | (II) $1 \mathrm{~nm}$ to $10^{-3} \mathrm{~nm}$ |
| (C) X-Ray | (III) $1 \mathrm{~mm}$ to $700 \mathrm{~nm}$ |
| (D) Infra-red | (IV) $0.1 \mathrm{~m}$ to $1 \mathrm{~mm}$ |
Choose the correct answer from the options given below:
In an electromagnetic wave, at an instant and at particular position, the electric field is along the negative $$z$$-axis and magnetic field is along the positive $$x$$-axis. Then the direction of propagation of electromagnetic wave is:
Which of the following Maxwell's equation is valid for time varying conditions but not valid for static conditions :
Given below are two statements: one is labelled as Assertion $$\mathbf{A}$$ and the other is labelled as Reason $$\mathbf{R}$$
Assertion A : EM waves used for optical communication have longer wavelengths than that of microwave, employed in Radar technology.
Reason R : Infrared EM waves are more energetic than microwaves, (used in Radar)
In the light of given statements, choose the correct answer from the options given below.
A plane electromagnetic wave of frequency $$20 ~\mathrm{MHz}$$ propagates in free space along $$\mathrm{x}$$-direction. At a particular space and time, $$\overrightarrow{\mathrm{E}}=6.6 \hat{j} \mathrm{~V} / \mathrm{m}$$. What is $$\overrightarrow{\mathrm{B}}$$ at this point?
The electric field in an electromagnetic wave is given as
$$\overrightarrow{\mathrm{E}}=20 \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{c}}\right) \overrightarrow{\mathrm{j}} \mathrm{NC}^{-1}$$
where $$\omega$$ and $$c$$ are angular frequency and velocity of electromagnetic wave respectively. The energy contained in a volume of $$5 \times 10^{-4} \mathrm{~m}^{3}$$ will be
(Given $$\varepsilon_{0}=8.85 \times 10^{-12} \mathrm{C}^{2} / \mathrm{Nm}^{2}$$ )
The amplitude of magnetic field in an electromagnetic wave propagating along y-axis is $$6.0 \times 10^{-7} \mathrm{~T}$$. The maximum value of electric field in the electromagnetic wave is
The energy of an electromagnetic wave contained in a small volume oscillates with
The energy density associated with electric field $$\vec{E}$$ and magnetic field $$\vec{B}$$ of an electromagnetic wave in free space is given by $$\left(\epsilon_{0}-\right.$$ permittivity of free space, $$\mu_{0}-$$ permeability of free space)
For the plane electromagnetic wave given by $$E=E_{0} \sin (\omega t-k x)$$ and $$B=B_{0} \sin (\omega t-k x)$$, the ratio of average electric energy density to average magnetic energy density is
The ratio of average electric energy density and total average energy density of electromagnetic wave is :
Match List I with List II :
| List I | List II | ||
|---|---|---|---|
| A. | Microwaves | I. | Radio active decay of the nucleus |
| B. | Gamma rays | II. | Rapid acceleration and deceleration of electron in aerials |
| C. | Radio waves | III. | Inner shell electrons |
| D. | X-rays | IV. | Klystron valve |
Choose the correct answer from the options given below :
| LIST I | LIST II | ||
|---|---|---|---|
| A. | Microwaves | I. | Physiotherapy |
| B. | UV rays | II. | Treatment of cancer |
| C. | Infra-red light | III. | Lasik eye surgery |
| D. | X-ray | IV. | Aircraft navigation |
Choose the correct answer from the options given below:
Given below are two statements :
Statement I : Electromagnetic waves are not deflected by electric and magnetic field.
Statement II : The amplitude of electric field and the magnetic field in electromagnetic waves are related to each other as $${E_0} = \sqrt {{{{\mu _0}} \over {{\varepsilon _0}}}} {B_0}$$.
In the light of the above statements, choose the correct answer from the options given below :
Which of the following are true?
A. Speed of light in vacuum is dependent on the direction of propagation.
B. Speed of light in a medium is independent of the wavelength of light.
C. The speed of light is independent of the motion of the source.
D. The speed of light in a medium is independent of intensity.
Choose the correct answer from the options given below:
Match List I with List II
| List I | List II | ||
|---|---|---|---|
| A. | Gauss's Law in Electrostatics | I. | $$\oint {\overrightarrow E \,.\,d\overrightarrow l = - {{d{\phi _B}} \over {dt}}} $$ |
| B. | Faraday's Law | II. | $$\oint {\overrightarrow B \,.\,d\overrightarrow A = 0} $$ |
| C. | Gauss's Law in Magnetism | III. | $$\oint {\overrightarrow B \,.\,d\overrightarrow l = {\mu _0}{i_c} + {\mu _0}{ \in _0}{{d{\phi _E}} \over {dt}}} $$ |
| D. | Ampere-Maxwell Law | IV. | $$\oint {\overrightarrow E \,.\,d\overrightarrow s = {q \over {{ \in _0}}}} $$ |
Choose the correct answer from the options given below :
An electromagnetic wave is transporting energy in the negative $$z$$ direction. At a certain point and certain time the direction of electric field of the wave is along positive $$y$$ direction. What will be the direction of the magnetic field of the wave at that point and instant?
The electric field and magnetic field components of an electromagnetic wave going through vacuum is described by
$$\mathrm{{E_x} = {E_o}\sin (kz - \omega t)}$$
$$\mathrm{{B_y} = {B_o}\sin (kz - \omega t)}$$
Then the correct relation between E$$_0$$ and B$$_0$$ is given by
In $$\overrightarrow E $$ and $$\overrightarrow K $$ represent electric field and propagation vectors of the EM waves in vacuum, then magnetic field vector is given by :
($$\omega$$ - angular frequency) :
Match List - I with List - II :
| List - I | List - II | ||
|---|---|---|---|
| (a) | UV rays | (i) | Diagnostic tool in medicine |
| (b) | X-rays | (ii) | Water purification |
| (c) | Microwave | (iii) | Communication, Radar |
| (d) | Infrared wave | (iv) | Improving visibility in foggy days |
Choose the correct answer from the options given below :
Sun light falls normally on a surface of area $$36 \mathrm{~cm}^{2}$$ and exerts an average force of $$7.2 \times 10^{-9} \mathrm{~N}$$ within a time period of 20 minutes. Considering a case of complete absorption, the energy flux of incident light is
Identify the correct statements from the following descriptions of various properties of electromagnetic waves.
(A) In a plane electromagnetic wave electric field and magnetic field must be perpendicular to each other and direction of propagation of wave should be along electric field or magnetic field.
(B) The energy in electromagnetic wave is divided equally between electric and magnetic fields.
(C) Both electric field and magnetic field are parallel to each other and perpendicular to the direction of propagation of wave.
(D) The electric field, magnetic field and direction of propagation of wave must be perpendicular to each other.
(E) The ratio of amplitude of magnetic field to the amplitude of electric field is equal to speed of light.
Choose the most appropriate answer from the options given below :
A beam of light travelling along $$X$$-axis is described by the electric field $$E_{y}=900 \sin \omega(\mathrm{t}-x / c)$$. The ratio of electric force to magnetic force on a charge $$\mathrm{q}$$ moving along $$Y$$-axis with a speed of $$3 \times 10^{7} \mathrm{~ms}^{-1}$$ will be :
(Given speed of light $$=3 \times 10^{8} \mathrm{~ms}^{-1}$$)
The oscillating magnetic field in a plane electromagnetic wave is given by
$$B_{y}=5 \times 10^{-6} \sin 1000 \pi\left(5 x-4 \times 10^{8} t\right) T$$. The amplitude of electric field will be :
A velocity selector consists of electric field $$\vec{E}=E \,\hat{k}$$ and magnetic field $$\vec{B}=B \,\hat{j}$$ with $$B=12 \,m T$$. The value of $$E$$ required for an electron of energy $$728 \,\mathrm{e} V$$ moving along the positive $$x$$-axis to pass undeflected is :
(Given, mass of electron $$=9.1 \times 10^{-31} \mathrm{~kg}$$ )
The magnetic field of a plane electromagnetic wave is given by :
$$ \overrightarrow{\mathrm{B}}=2 \times 10^{-8} \sin \left(0.5 \times 10^{3} x+1.5 \times 10^{11} \mathrm{t}\right) \,\hat{j} \mathrm{~T}$$.
The amplitude of the electric field would be :
Light wave travelling in air along x-direction is given by $${E_y} = 540\sin \pi \times {10^4}(x - ct)\,V{m^{ - 1}}$$. Then, the peak value of magnetic field of wave will be (Given c = 3 $$\times$$ 108 ms$$-$$1)
The rms value of conduction current in a parallel plate capacitor is $$6.9 \,\mu \mathrm{A}$$. The capacity of this capacitor, if it is connected to $$230 \mathrm{~V}$$ ac supply with an angular frequency of $$600 \,\mathrm{rad} / \mathrm{s}$$, will be :
An expression for oscillating electric field in a plane electromagnetic wave is given as Ez = 300 sin(5$$\pi$$ $$\times$$ 103x $$-$$ 3$$\pi$$ $$\times$$ 1011t) Vm$$-$$1
Then, the value of magnetic field amplitude will be :
(Given : speed of light in Vacuum c = 3 $$\times$$ 108 ms$$-$$1)
An EM wave propagating in x-direction has a wavelength of 8 mm. The electric field vibrating y-direction has maximum magnitude of 60 Vm$$-$$1. Choose the correct equations for electric and magnetic fields if the EM wave is propagating in vacuum :
A radar sends an electromagnetic signal of electric field (E0) = 2.25 V/m and magnetic field (B0) = 1.5 $$\times$$ 10$$-$$8 T which strikes a target on line of sight at a distance of 3 km in a medium. After that, a part of signal (echo) reflects back towards the radar with same velocity and by same path. If the signal was transmitted at time t = 0 from radar, then after how much time echo will reach to the radar?
Given below are two statements :
Statement I : A time varying electric field is a source of changing magnetic field and vice-versa. Thus a disturbance in electric or magnetic field creates EM waves.
Statement II : In a material medium, the EM wave travels with speed $$v = {1 \over {\sqrt {{\mu _0}{ \in _0}} }}$$. In the light of the above statements, choose the correct answer from the options given below.
Match List-I with List-II :
| List - I | List - II | ||
|---|---|---|---|
| (a) | Ultraviolet rays | (i) | Study crystal structure |
| (b) | Microwaves | (ii) | Greenhouse effect |
| (c) | Infrared rays | (iii) | Sterilizing surgical instrument |
| (d) | X-rays | (iv) | Radar system |
Choose the correct answer from the options given below :
Which is the correct ascending order of wavelengths?
If Electric field intensity of a uniform plane electromagnetic wave is given as $$E = - 301.6\sin (kz - \omega t){\widehat a_x} + 452.4\sin (kz - \omega t){\widehat a_y}{V \over m}$$. Then magnetic intensity 'H' of this wave in Am$$-$$1 will be :
[Given : Speed of light in vacuum $$c = 3 \times {10^8}$$ ms$$-$$1, Permeability of vacuum $${\mu _0} = 4\pi \times {10^{ - 7}}$$ NA$$-$$2]
In free space, an electromagnetic wave of 3 GHz frequency strikes over the edge of an object of size $${\lambda \over {100}}$$, where $$\lambda$$ is the wavelength of the wave in free space. The phenomenon, which happens there will be :
The electromagnetic waves travel in a medium at a speed of 2.0 $$\times$$ 108 m/s. The relative permeability of the medium is 1.0. The relative permittivity of the medium will be :
The electric field in an electromagnetic wave is given by E = 56.5 sin $$\omega$$(t $$-$$ x/c) NC$$-$$1. Find the intensity of the wave if it is propagating along x-axis in the free space.
(Given : $$\varepsilon $$0 = 8.85 $$\times$$ 10$$-$$12C2N$$-$$1m$$-$$2)
An electric bulb is rated as 200 W. What will be the peak magnetic field at 4 m distance produced by the radiations coming from this bulb? Consider this bulb as a point source with 3.5% efficiency.
A plane electromagnetic wave travels in a medium of relative permeability 1.61 and relative permittivity 6.44. If magnitude of magnetic intensity is 4.5 $$\times$$ 10$$-$$2 Am$$-$$1 at a point, what will be the approximate magnitude of electric field intensity at that point?
(Given : Permeability of free space $$\mu$$0 = 4$$\pi$$ $$\times$$ 10$$-$$7 NA$$-$$2, speed of light in vacuum c = 3 $$\times$$ 108 ms$$-$$1)
E = 20cos(2 $$\times$$ 1010 t $$-$$ 200x) V/m. The dielectric constant of the medium is equal to : (Take $$\mu$$r = 1)
(Given C = speed of light in vacuum)
(Given $$\mu$$r = 1)
$$E = 3.1\cos \left[ {(1.8)z - (5.4 \times {{10}^6})t} \right]\widehat iN/C$$
is incident normally on a perfectly reflecting wall at z = a. Choose the correct option
($${\varepsilon _0} = 8.85 \times {10^{ - 12}}{C^2}{N^{ - 1}}{m^{ - 2}}$$)
$$\overrightarrow B $$ = 8.0 $$\times$$ 10$$-$$8 $$\widehat z$$T. The value of electric field at this point is :
(speed of light = 3 $$\times$$ 108 ms$$-$$1)
$$\widehat x$$, $$\widehat y$$, $$\widehat z$$ are unit vectors along x, y and z directions.
| List I | List II | ||
|---|---|---|---|
| (a) | Source of microwave frequency | (i) | Radioactive decay of nucleus |
| (b) | Source of infrared frequency | (ii) | Magnetron |
| (c) | Source of Gamma Rays | (iii) | Inner shell electrons |
| (d) | Source of X-rays | (iv) | Vibration of atoms and molecules |
| (v) | LASER | ||
| (vi) | RC circuit |
Choose the correct answer from the options given below :
$$\overrightarrow B \left( {x,t} \right)$$ = $$\left[ {1.2 \times {{10}^{ - 7}}\sin \left( {0.5 \times {{10}^3}x + 1.5 \times {{10}^{11}}t} \right)\widehat k} \right]$$ T
The instantaneous electric field $$\overrightarrow E $$ corresponding to $$\overrightarrow B $$ is :
(speed of light c = 3 × 108 ms–1)
| I | II |
|---|---|
| Radiation | Wavelength |
| (a) Microwave | (i) 100 m |
| (b) Gamma rays | (ii) 10–15 m |
| (c) A.M. radio waves | (iii) 10–10 m |
| (d) X-rays | (iv) 10–3 m |
$$\overrightarrow E = 30\widehat j\sin \left( {1.5 \times {{10}^7}t - 5 \times {{10}^{ - 2}}x} \right)$$ V/m.
The maximum magnetic force experienced by the electron will be :
(given c = 3 $$ \times $$ 108 ms–1 and electron charge = 1.6 $$ \times $$ 10–19 C)
$$\overrightarrow E = {E_0}\left( {\widehat x + \widehat y} \right)\sin \left( {kz - \omega t} \right)$$
Its magnetic field will be given by :
$$\overrightarrow E = {E_0}\widehat j\cos \left( {\omega t - kx} \right)$$.
The magnetic field $$\overrightarrow B $$ , at the moment t = 0 is :
$$\overrightarrow B = 3 \times {10^{ - 8}}\sin \left[ {200\pi \left( {y + ct} \right)} \right]\widehat i$$ T
where c = 3 $$ \times $$ 108 ms–1 is the speed of light. The corresponding electric field is :
frequency of 2.0 $$ \times $$ 1010 Hz and its energy density is 1.02 $$ \times $$ 10–8 J/m3 in vacuum. The amplitude of the magnetic field of the wave is close to
( $${1 \over {4\pi {\varepsilon _0}}} = 9 \times {10^9}{{N{m^2}} \over {{C^2}}}$$ and speed of light
= 3 $$ \times $$ 108 ms–1)
$$\overrightarrow {{E_1}} = {E_0}\widehat j\cos \left( {\omega t - kx} \right)$$ and
$$\overrightarrow {{E_2}} = {E_0}\widehat k\cos \left( {\omega t - ky} \right)$$
At t = 0, a particle of charge q is at origin with
a velocity $$\overrightarrow v = 0.8c\widehat j$$ (c is the speed of light in vacuum). The instantaneous force experienced by the particle is :
$$\overrightarrow E = {E_0}{{\widehat i + \widehat j} \over {\sqrt 2 }}\cos \left( {kz + \omega t} \right)$$
At t = 0, a positively charged particle is at the point (x, y, z) = $$\left( {0,0,{\pi \over k}} \right)$$.
If its instantaneous velocity at (t = 0) is $${v_0}\widehat k$$ , the force acting on it due to the wave is :
$$\overrightarrow B $$ = 3 $$ \times $$ 10-8 sin(1.6 $$ \times $$ 103x + 48 $$ \times $$ 1010t)$$\widehat j$$ T, then what will be expression for electric field ?
$$\overrightarrow E = {E_0}\widehat i\cos (kz)cos(\omega t)$$
The corresponding magnetic field $$\overrightarrow B $$ is then given by
$$$\overline B = {B_0}\widehat i\left[ {\cos (kz - \omega t)} \right] + {B_i}\widehat j\cos (kz + \omega t)$$$ B0 = 3 × 10–5 T and B1 = 2 × 10–6 T.
The rms value of the force experienced by a stationary charge Q = 10–4 C at z = 0 is closest to :
$$\mathop B\limits^ \to = 1.6 \times {10^{ - 6}}\cos \left( {2 \times {{10}^7}z + 6 \times {{10}^{15}}t} \right)\left( {2\mathop i\limits^ \wedge + \mathop j\limits^ \wedge } \right){{Wb} \over {{m^2}}}$$
The associated electric field will be :-
[Given permittivity of space $$ \in $$0 = 9 $$ \times $$ 10–12 SI units, Speed of light c = 3 $$ \times $$ 108 m/s]
$$\overrightarrow {{E_1}} $$ = $${E_{01}}\widehat x\cos \left[ {2\pi v\left( {{z \over c} - t} \right)} \right]$$ in air and
$$\overrightarrow {{E_2}} $$ = $${E_{02}}\widehat x\cos \left[ {k\left( {2z - ct} \right)} \right]$$ in medium,
where the wave number k and frequency $$\nu $$ refer to their values in air. The medium is non-magnetic. If $${\varepsilon _{{r_1}}}$$ and $${\varepsilon _{{r_2}}}$$ refer to relative permittivities of air and medium respectively, which of the following options is correct ?
It is polarized along the $$\widehat k$$ direction. The acceptable form for the magnetic field is :
$$\overrightarrow E $$ = 2 E0 $$\widehat i$$ cos kz cos $$\omega $$t
Its magnetic field $$\overrightarrow B $$ is then given by :
$$\overrightarrow B $$ = B0 sin (k x + $$\omega $$t) $$\widehat j\,T$$
Expression for corresponding electric field will be :
Where c is speed of light.
A : Blue light B : Yellow light
C : X-ray D : Radiowave.
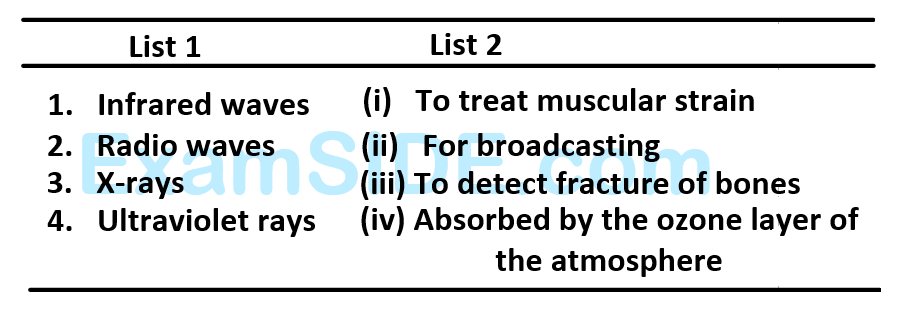
Numerical
A time varying potential difference is applied between the plates of a parallel plate capacitor of capacitance $2.5 \mu \mathrm{~F}$. The dielectric constant of the medium between the capacitor plates is 1 . It produces an instantaneous displacement current of 0.25 mA in the intervening space between the capacitor plates, the magnitude of the rate of change of the potential difference will be _________ $\mathrm{Vs}^{-1}$.
A parallel plate capacitor of area $A=16 \mathrm{~cm}^2$ and separation between the plates 10 cm , is charged by a DC current. Consider a hypothetical plane surface of area $\mathrm{A}_0=3.2 \mathrm{~cm}^2$ inside the capacitor and parallel to the plates. At an instant, the current through the circuit is 6A. At the same instant the displacement current through $\mathrm{A}_0$ is __________ mA .
In a medium the speed of light wave decreases to $$0.2$$ times to its speed in free space The ratio of relative permittivity to the refractive index of the medium is $$x: 1$$. The value of $$x$$ is _________.
(Given speed of light in free space $$=3 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}$$ and for the given medium $$\mu_{\mathrm{r}}=1$$)
A point source of light is placed at the centre of curvature of a hemispherical surface. The source emits a power of $$24 \mathrm{~W}$$. The radius of curvature of hemisphere is $$10 \mathrm{~cm}$$ and the inner surface is completely reflecting. The force on the hemisphere due to the light falling on it is ____________ $$\times~10^{-8} \mathrm{~N}$$.
Nearly 10% of the power of a $$110 \mathrm{~W}$$ light bulb is converted to visible radiation. The change in average intensities of visible radiation, at a distance of $$1 \mathrm{~m}$$ from the bulb to a distance of $$5 \mathrm{~m}$$ is $$a \times 10^{-2} \mathrm{~W} / \mathrm{m}^{2}$$. The value of 'a' will be _________.
The displacement current of 4.425 $$\mu$$A is developed in the space between the plates of parallel plate capacitor when voltage is changing at a rate of 106 Vs$$-$$1. The area of each plate of the capacitor is 40 cm2. The distance between each plate of the capacitor is x $$\times$$ 10$$-$$3 m. The value of x is __________.
(Permittivity of free space, E0 = 8.85 $$\times$$ 10$$-$$12 C2 N$$-$$1 m$$-$$2).
The intensity of the light from a bulb incident on a surface is 0.22 W/m2. The amplitude of the magnetic field in this light-wave is ______________ $$\times$$ 10$$-$$9 T.
(Given : Permittivity of vacuum $$\in$$0 = 8.85 $$\times$$ 10$$-$$12 C2 N$$-$$1-m$$-$$2, speed of light in vacuum c = 3 $$\times$$ 108 ms$$-$$1)
The energy contained in a cylinder of volume V is 5.5 $$\times$$ 10$$-$$12 J. The value of V is _____________ cm3. (given $$\in$$0 = 8.8 $$\times$$ 10$$-$$12C2N$$-$$1m$$-$$2)
$$\overrightarrow E = 200\cos \left[ {\left( {{{0.5 \times {{10}^3}} \over m}} \right)x - \left( {1.5 \times {{10}^{11}}{{rad} \over s} \times t} \right)} \right]{V \over m}\widehat j$$. If this wave falls normally on a perfectly reflecting surface having an area of 100 cm2. If the radiation pressure exerted by the E.M. wave on the surface during a 10 minute exposure is $${x \over {{{10}^9}}}{N \over {{m^2}}}$$. Find the value of x .
(Assume complete absorption and normal incidence conditions are there)
The rms electric field, in units of V/m associated with this source is close to the nearest integer is __________.
$$ \in $$0 = 8.86 × 10–12 C2 Nm–2; c = 3 × 108 ms–1)