Magnetic Effect of Current · Physics · JEE Main
MCQ (Single Correct Answer)
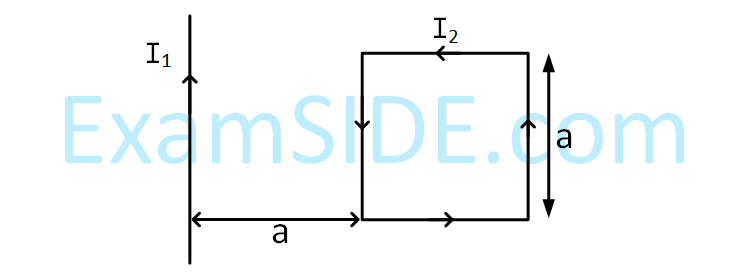
Figure shows a current carrying square loop ABCD of edge length is ‘a’ lying in a plane. If the resistance of the ABC part is r and that of ADC part is 2r, then the magnitude of the resultant magnetic field at centre of the square loop is

A particle of charge $q$, mass $m$ and kinetic energy $E$ enters in magnetic field perpendicular to its velocity and undergoes a circular arc of radius (r). Which of the following curves represents the variation of $r$ with $E$ ?
Uniform magnetic fields of different strengths $\left(B_1\right.$ and $\left.B_2\right)$, both normal to the plane of the paper exist as shown in the figure. A charged particle of mass $m$ and charge $q$, at the interface at an instant, moves into the region 2 with velocity $v$ and returns to the interface. It continues to move into region 1 and finally reaches the interface. What is the displacement of the particle during this movement along the interface?

(Consider the velocity of the particle to be normal to the magnetic field and $\mathrm{B}_2>\mathrm{B}_1$ )
Given below are two statements: one is labelled as $\mathbf{A s s e r t i o n} \mathbf{A}$ and the other is labelled as Reason $\mathbf{R}$
Assertion A : If Oxygen ion $\left(\mathrm{O}^{-2}\right)$ and Hydrogen ion $\left(\mathrm{H}^{+}\right)$enter normal to the magnetic field with equal momentum, then the path of $\mathrm{O}^{-2}$ ion has a smaller curvature than that of $\mathrm{H}^{+}$.
Reason R : A proton with same linear momentum as an electron will form a path of smaller radius of curvature on entering a uniform magnetic field perpendicularly.
In the light of the above statements, choose the correct answer from the options given below
In a moving coil galvanometer, two moving coils $\mathrm{M}_1$ and $\mathrm{M}_2$ have the following particulars :
$$ \begin{aligned} & \mathrm{R}_1=5 \Omega, \mathrm{~N}_1=15, \mathrm{~A}_1=3.6 \times 10^{-3} \mathrm{~m}^2, \mathrm{~B}_1=0.25 \mathrm{~T} \\ & \mathrm{R}_2=7 \Omega, \mathrm{~N}_2=21, \mathrm{~A}_2=1.8 \times 10^{-3} \mathrm{~m}^2, \mathrm{~B}_2=0.50 \mathrm{~T} \end{aligned} $$
Assuming that torsional constant of the springs are same for both coils, what will be the ratio of voltage sensitivity of $M_1$ and $M_2$ ?
Let $B_1$ be the magnitude of magnetic field at center of a circular coil of radius $R$ carrying current I. Let $\mathrm{B}_2$ be the magnitude of magnetic field at an axial distance ' $x$ ' from the center. For $x: \mathrm{R}=3: 4, \frac{\mathrm{~B}_2}{\mathrm{~B}_1}$ is :
Consider a long straight wire of a circular cross-section (radius a) carrying a steady current I. The current is uniformly distributed across this cross-section. The distances from the centre of the wire’s cross-section at which the magnetic field [inside the wire, outside the wire] is half of the maximum possible magnetic field, any where due to the wire, will be :

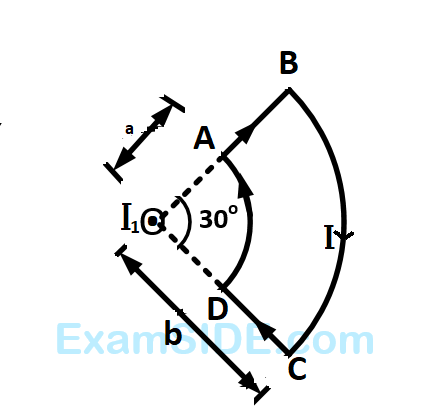
An infinite wire has a circular bend of radius a, and carrying a current I as shown in the figure. The magnitude of magnetic field at the origin O of the arc is given by:
Consider a long thin conducting wire carrying a uniform current I. A particle having mass "M" and charge " $q$ " is released at a distance " $a$ " from the wire with a speed $v_0$ along the direction of current in the wire. The particle gets attracted to the wire due to magnetic force. The particle turns round when it is at distance $x$ from the wire. The value of $x$ is [ $\mu_0$ is vacuum permeability]

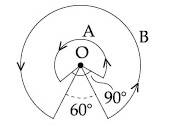
N equally spaced charges each of value q , are placed on a circle of radius R . The circle rotates about its axis with an angular velocity $\omega$ as shown in the figure. A bigger Amperian loop B encloses the whole circle where as a smaller Amperian loop A encloses a small segment. The difference between enclosed currents, $I_A-I_B$, for the given Amperian loops is
Given below are two statements. One is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : A electron in a certain region of uniform magnetic field is moving with constant velocity in a straight line path.
Reason (R) : The magnetic field in that region is along the direction of velocity of the electron. In the light of the above statements, choose the correct answer from the options given below :
A long straight wire of a circular cross-section with radius ' a ' carries a steady current I . The current I is uniformly distributed across this cross-section. The plot of magnitude of magnetic field B with distance $r$ from the centre of the wire is given by
An electron projected perpendicular to a uniform magnetic field B moves in a circle. If Bohr's quantization is applicable, then the radius of the electronic orbit in the first excited state is :
A proton and a deutron $$(q=+\mathrm{e}, m=2.0 \mathrm{u})$$ having same kinetic energies enter a region of uniform magnetic field $$\vec{B}$$, moving perpendicular to $$\vec{B}$$. The ratio of the radius $$r_d$$ of deutron path to the radius $$r_p$$ of the proton path is:
Given below are two statements :
Statement (I) : When currents vary with time, Newton's third law is valid only if momentum carried by the electromagnetic field is taken into account
Statement (II) : Ampere's circuital law does not depend on Biot-Savart's law.
In the light of the above statements, choose the correct answer from the options given below :
A long straight wire of radius a carries a steady current I. The current is uniformly distributed across its cross section. The ratio of the magnetic field at $$\frac{a}{2}$$ and $$2 a$$ from axis of the wire is :
An element $$\Delta l=\Delta x\hat{i}$$ is placed at the origin and carries a large current $$I=10 \mathrm{~A}$$. The magnetic field on the $$y$$-axis at a distance of $$0.5 \mathrm{~m}$$ from the elements $$\Delta x$$ of $$1 \mathrm{~cm}$$ length is:

The electrostatic force $$\left(\vec{F_1}\right)$$ and magnetic force $$\left(\vec{F}_2\right)$$ acting on a charge $$q$$ moving with velocity $$v$$ can be written :
An electron is projected with uniform velocity along the axis inside a current carrying long solenoid. Then :
A uniform magnetic field of $$2 \times 10^{-3} \mathrm{~T}$$ acts along positive $$Y$$-direction. A rectangular loop of sides $$20 \mathrm{~cm}$$ and $$10 \mathrm{~cm}$$ with current of $$5 \mathrm{~A}$$ is in $$Y-Z$$ plane. The current is in anticlockwise sense with reference to negative $$X$$ axis. Magnitude and direction of the torque is:
A rigid wire consists of a semicircular portion of radius $$R$$ and two straight sections. The wire is partially immerged in a perpendicular magnetic field $$B=B_0 \hat{k}$$ as shown in figure. The magnetic force on the wire if it has a current $$i$$ is:

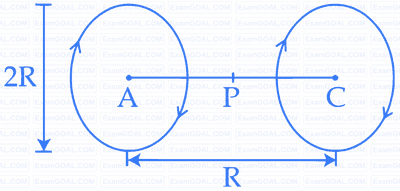
Two insulated circular loop A and B of radius '$$a$$' carrying a current of '$$\mathrm{I}$$' in the anti clockwise direction as shown in the figure. The magnitude of the magnetic induction at the centre will be :

Two particles $$X$$ and $$Y$$ having equal charges are being accelerated through the same potential difference. Thereafter they enter normally in a region of uniform magnetic field and describes circular paths of radii $$R_1$$ and $$R_2$$ respectively. The mass ratio of $$X$$ and $$Y$$ is :
A proton moving with a constant velocity passes through a region of space without any change in its velocity. If $$\overrightarrow{\mathrm{E}}$$ and $$\overrightarrow{\mathrm{B}}$$ represent the electric and magnetic fields respectively, then the region of space may have :
(A) $$\mathrm{E}=0, \mathrm{~B}=0$$
(B) $$\mathrm{E}=0, \mathrm{~B} \neq 0$$
(C) $$\mathrm{E} \neq 0, \mathrm{~B}=0$$
(D) $$\mathrm{E} \neq 0, \mathrm{~B} \neq 0$$
Choose the most appropriate answer from the options given below :
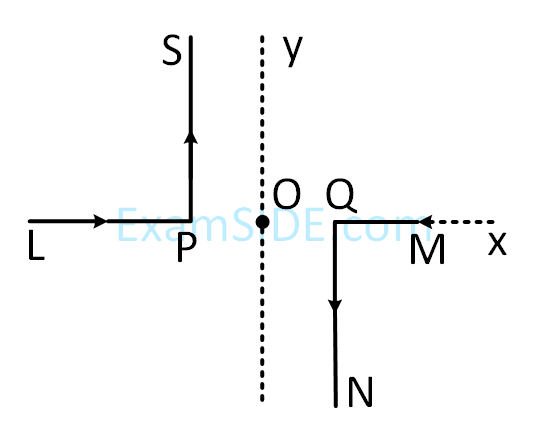
An electron is moving along the positive $$\mathrm{x}$$-axis. If the uniform magnetic field is applied parallel to the negative z-axis, then
A. The electron will experience magnetic force along positive y-axis
B. The electron will experience magnetic force along negative y-axis
C. The electron will not experience any force in magnetic field
D. The electron will continue to move along the positive $$\mathrm{x}$$-axis
E. The electron will move along circular path in magnetic field
Choose the correct answer from the options given below:
The source of time varying magnetic field may be
(A) a permanent magnet
(B) an electric field changing linearly with time
(C) direct current
(D) a decelerating charge particle
(E) an antenna fed with a digital signal
Choose the correct answer from the options given below:
An electron is allowed to move with constant velocity along the axis of current carrying straight solenoid.
A. The electron will experience magnetic force along the axis of the solenoid.
B. The electron will not experience magnetic force.
C. The electron will continue to move along the axis of the solenoid.
D. The electron will be accelerated along the axis of the solenoid.
E. The electron will follow parabolic path-inside the solenoid.
Choose the correct answer from the options given below:
A charge particle moving in magnetic field B, has the components of velocity along B as well as perpendicular to B. The path of the charge particle will be
A long straight wire of circular cross-section (radius a) is carrying steady current I. The current I is uniformly distributed across this cross-section. The magnetic field is
As shown in the figure, a long straight conductor with semicircular arc of radius $$\frac{\pi}{10}$$m is carrying current $$\mathrm{I=3A}$$. The magnitude of the magnetic field, at the center O of the arc is :
(The permeability of the vacuum $$=4\pi\times10^{-7}~\mathrm{NA}^{-2}$$)

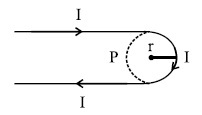
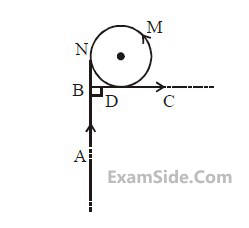
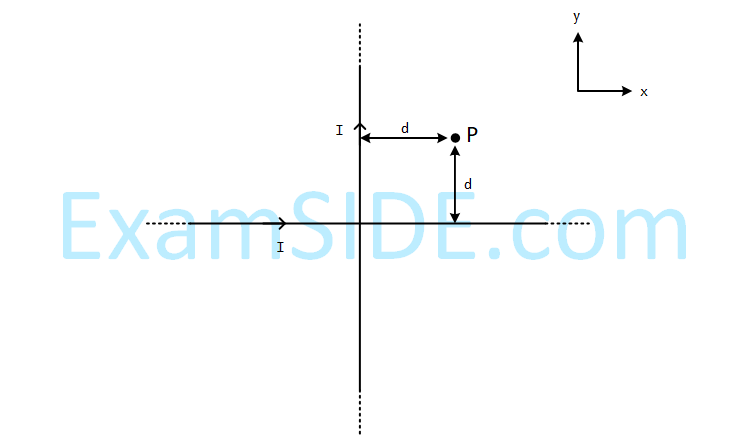
Find the magnetic field at the point $$\mathrm{P}$$ in figure. The curved portion is a semicircle connected to two long straight wires.

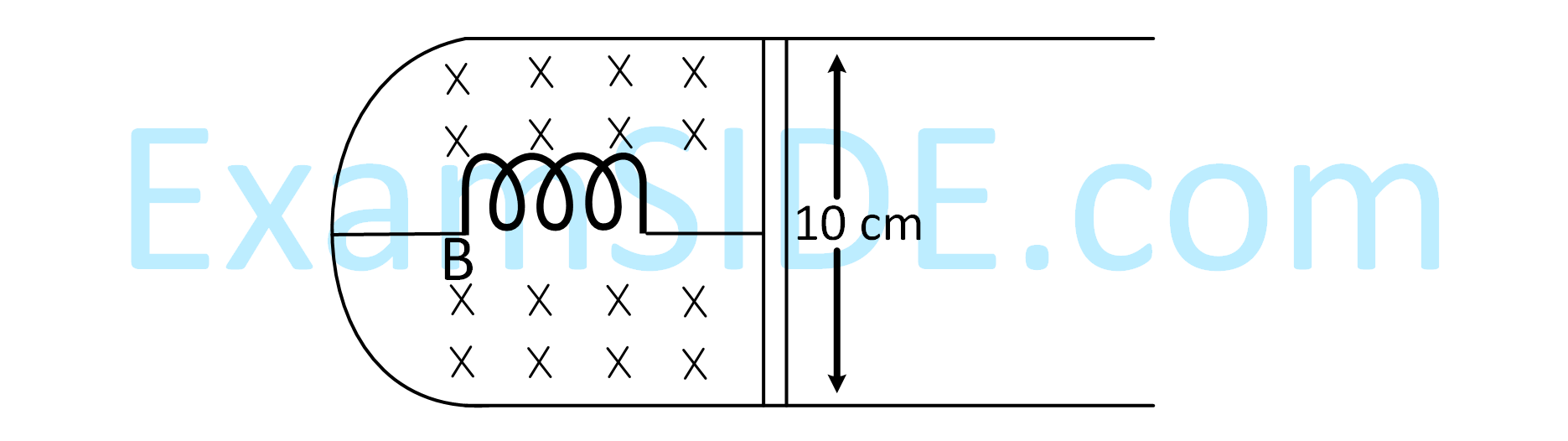
A rod with circular cross-section area $$2 \mathrm{~cm}^{2}$$ and length $$40 \mathrm{~cm}$$ is wound uniformly with 400 turns of an insulated wire. If a current of $$0.4 \mathrm{~A}$$ flows in the wire windings, the total magnetic flux produced inside windings is $$4 \pi \times 10^{-6} \mathrm{~Wb}$$. The relative permeability of the rod is
(Given : Permeability of vacuum $$\mu_{0}=4 \pi \times 10^{-7} \mathrm{NA}^{-2}$$)
As shown in the figure, a current of $2 \mathrm{~A}$ flowing in an equilateral triangle of side $4 \sqrt{3} \mathrm{~cm}$. The magnetic field at the centroid $\mathrm{O}$ of the triangle is

(Neglect the effect of earth's magnetic field)
A current carrying rectangular loop PQRS is made of uniform wire. The length $P R=Q S=5 \mathrm{~cm}$ and $P Q=R S=100 \mathrm{~cm}$. If ammeter current reading changes from I to $2 I$, the ratio of magnetic forces per unit length on the wire $P Q$ due to wire $R S$ in the two cases respectively $\left(f_{P Q}^I: f_{P Q}^{2 t}\right)$ is:

A massless square loop, of wire of resistance $$10 \Omega$$, supporting a mass of $$1 \mathrm{~g}$$, hangs vertically with one of its sides in a uniform magnetic field of $$10^{3} \mathrm{G}$$, directed outwards in the shaded region. A dc voltage $$\mathrm{V}$$ is applied to the loop. For what value of $$\mathrm{V}$$, the magnetic force will exactly balance the weight of the supporting mass of $$1 \mathrm{~g}$$ ?
(If sides of the loop $$=10 \mathrm{~cm}, \mathrm{~g}=10 \mathrm{~ms}^{-2}$$)

The magnetic moments associated with two closely wound circular coils $$\mathrm{A}$$ and $$\mathrm{B}$$ of radius $$\mathrm{r}_{\mathrm{A}}=10$$ $$\mathrm{cm}$$ and $$\mathrm{r}_{\mathrm{B}}=20 \mathrm{~cm}$$ respectively are equal if : (Where $$\mathrm{N}_{\mathrm{A}}, \mathrm{I}_{\mathrm{A}}$$ and $$\mathrm{N}_{\mathrm{B}}, \mathrm{I}_{\mathrm{B}}$$ are number of turn and current of $$\mathrm{A}$$ and $$\mathrm{B}$$ respectively)
The electric current in a circular coil of four turns produces a magnetic induction 32 T at its centre. The coil is unwound and is rewound into a circular coil of single turn, the magnetic induction at the centre of the coil by the same current will be :
The magnitude of magnetic induction at mid point $$\mathrm{O}$$ due to current arrangement as shown in Fig will be

A single current carrying loop of wire carrying current I flowing in anticlockwise direction seen from +ve $$\mathrm{z}$$ direction and lying in $$x y$$ plane is shown in figure. The plot of $$\hat{j}$$ component of magnetic field (By) at a distance '$$a$$' (less than radius of the coil) and on $$y z$$ plane vs $$z$$ coordinate looks like

For a moving coil galvanometer, the deflection in the coil is 0.05 rad when a current of 10 mA is passes through it. If the torsional constant of suspension wire is $$4.0\times10^{-5}\mathrm{N~m~rad^{-1}}$$, the magnetic field is 0.01T and the number of turns in the coil is 200, the area of each turn (in cm$$^2$$) is :
Match List I with List II
| List I (Current configuration) |
List II (Magnitude of Magnetic Field at point O) |
||
|---|---|---|---|
| A. |  |
I. | $${B_0} = {{{\mu _0}I} \over {4\pi r}}[\pi + 2]$$ |
| B. |  |
II. | $${B_0} = {{{\mu _0}} \over {4 }}{I \over r}$$ |
| C. |  |
III. | $${B_0} = {{{\mu _0}I} \over {2\pi r}}[\pi - 1]$$ |
| D. |  |
IV. | $${B_0} = {{{\mu _0}I} \over {4\pi r}}[\pi + 1]$$ |
Choose the correct answer from the options given below :
A long solenoid is formed by winding 70 turns cm$$^{-1}$$. If 2.0 A current flows, then the magnetic field produced inside the solenoid is ____________ ($$\mu_0=4\pi\times10^{-7}$$ TmA$$^{-1}$$)
Two long straight wires P and Q carrying equal current 10A each were kept parallel to each other at 5 cm distance. Magnitude of magnetic force experienced by 10 cm length of wire P is F$$_1$$. If distance between wires is halved and currents on them are doubled, force F$$_2$$ on 10 cm length of wire P will be:
A circular loop of radius $$r$$ is carrying current I A. The ratio of magnetic field at the center of circular loop and at a distance r from the center of the loop on its axis is :
A wire X of length $$50 \mathrm{~cm}$$ carrying a current of $$2 \mathrm{~A}$$ is placed parallel to a long wire $$\mathrm{Y}$$ of length $$5 \mathrm{~m}$$. The wire $$\mathrm{Y}$$ carries a current of $$3 \mathrm{~A}$$. The distance between two wires is $$5 \mathrm{~cm}$$ and currents flow in the same direction. The force acting on the wire $$\mathrm{Y}$$ is

A triangular shaped wire carrying $$10 \mathrm{~A}$$ current is placed in a uniform magnetic field of $$0.5 \mathrm{~T}$$, as shown in figure. The magnetic force on segment $$\mathrm{CD}$$ is
(Given $$\mathrm{BC}=\mathrm{CD}=\mathrm{BD}=5 \mathrm{~cm}$$.)

The magnetic field at the center of current carrying circular loop is $$B_{1}$$. The magnetic field at a distance of $$\sqrt{3}$$ times radius of the given circular loop from the center on its axis is $$B_{2}$$. The value of $$B_{1} / B_{2}$$ will be
The current sensitivity of a galvanometer can be increased by :
(A) decreasing the number of turns
(B) increasing the magnetic field
(C) decreasing the area of the coil
(D) decreasing the torsional constant of the spring
Choose the most appropriate answer from the options given below :
As shown in the figure, a metallic rod of linear density $$0.45 \mathrm{~kg} \mathrm{~m}^{-1}$$ is lying horizontally on a smooth inclined plane which makes an angle of $$45^{\circ}$$ with the horizontal. The minimum current flowing in the rod required to keep it stationary, when $$0.15 \mathrm{~T}$$ magnetic field is acting on it in the vertical upward direction, will be :
{Use $$g=10 \mathrm{~m} / \mathrm{s}^{2}$$}

A cyclotron is used to accelerate protons. If the operating magnetic field is $$1.0 \mathrm{~T}$$ and the radius of the cyclotron 'dees' is $$60 \mathrm{~cm}$$, the kinetic energy of the accelerated protons in MeV will be :
$$[\mathrm{use} \,\,\mathrm{m}_{\mathrm{p}}=1.6 \times 10^{-27} \mathrm{~kg}, \mathrm{e}=1.6 \times 10^{-19} \,\mathrm{C}$$ ]
Two concentric circular loops of radii $$r_{1}=30 \mathrm{~cm}$$ and $$r_{2}=50 \mathrm{~cm}$$ are placed in $$\mathrm{X}-\mathrm{Y}$$ plane as shown in the figure. A current $$I=7 \mathrm{~A}$$ is flowing through them in the direction as shown in figure. The net magnetic moment of this system of two circular loops is approximately :

A charge particle is moving in a uniform magnetic field $$(2 \hat{i}+3 \hat{j}) \,\mathrm{T}$$. If it has an acceleration of $$(\alpha \hat{i}-4 \hat{j})\, \mathrm{m} / \mathrm{s}^{2}$$, then the value of $$\alpha$$ will be :
$$\mathrm{B}_{X}$$ and $$\mathrm{B}_{\mathrm{Y}}$$ are the magnetic fields at the centre of two coils $$\mathrm{X}$$ and $$\mathrm{Y}$$ respectively each carrying equal current. If coil $$X$$ has 200 turns and $$20 \mathrm{~cm}$$ radius and coil $$Y$$ has 400 turns and $$20 \mathrm{~cm}$$ radius, the ratio of $$B_{X}$$ and $$B_{Y}$$ is :
Two charged particles, having same kinetic energy, are allowed to pass through a uniform magnetic field perpendicular to the direction of motion. If the ratio of radii of their circular paths is $$6: 5$$ and their respective masses ratio is $$9: 4$$. Then, the ratio of their charges will be :
A coil of n number of turns wound tightly in the form of a spiral with inner and outer radii r1 and r2 respectively. When a current of strength I is passed through the coil, the magnetic field at its centre will be :
A cyclotron is working at a frequency of 10 MHz. If the radius of its dees is 60 cm. The maximum kinetic energy of accelerated proton will be :
(Take : e = 1.6 $$\times$$ 10$$-$$19 C, mp = 1.67 $$\times$$ 10$$-$$27 kg)
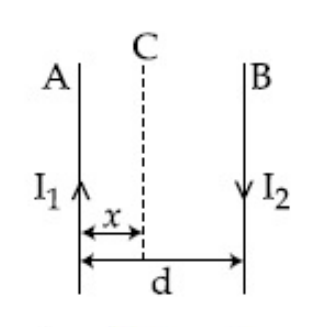
Two long current carrying conductors are placed to each other at a distance of 8 cm between them. The magnitude of magnetic field produced at mid-point between the two conductors due to current flowing in them is 300 $$\mu$$T. The equal current flowing in the two conductors is :
Given below are two statements :
Statement I : The electric force changes the speed of the charged particle and hence changes its kinetic energy; whereas the magnetic force does not change the kinetic energy of the charged particle.
Statement II : The electric force accelerates the positively charged particle perpendicular to the direction of electric field. The magnetic force accelerates the moving charged particle along the direction of magnetic field.
In the light of the above statements, choose the most appropriate answer from the options given below :
A charge particle moves along circular path in a uniform magnetic field in a cyclotron. The kinetic energy of the charge particle increases to 4 times its initial value. What will be the ratio of new radius to the original radius of circular path of the charge particle :
Two parallel, long wires are kept 0.20 m apart in vacuum, each carrying current of x A in the same direction. If the force of attraction per meter of each wire is 2 $$\times$$ 10$$-$$6 N, then the value of x is approximately :
An infinitely long hollow conducting cylinder with radius R carries a uniform current along its surface.
Choose the correct representation of magnetic field (B) as a function of radial distance (r) from the axis of cylinder.
Two long parallel conductors S1 and S2 are separated by a distance 10 cm and carrying currents of 4A and 2A respectively. The conductors are placed along x-axis in X-Y plane. There is a point P located between the conductors (as shown in figure).
A charge particle of 3$$\pi$$ coulomb is passing through the point P with velocity $$\overrightarrow v = (2\widehat i + 3\widehat j)$$ m/s; where $$\widehat i$$ and $$\widehat j$$ represents unit vector along x & y axis respectively.
The force acting on the charge particle is $$4\pi \times {10^{ - 5}}( - x\widehat i + 2\widehat j)$$ N. The value of x is :

A proton and an alpha particle of the same velocity enter in a uniform magnetic field which is acting perpendicular to their direction of motion. The ratio of the radii of the circular paths described by the alpha particle and proton is :
A long solenoid carrying a current produces a magnetic field B along its axis. If the current is doubled and the number of turns per cm is halved, the new value of magnetic field will be equal to
A long straight wire with a circular cross-section having radius R, is carrying a steady current I. The current I is uniformly distributed across this cross-section. Then the variation of magnetic field due to current I with distance r (r < R) from its centre will be :
A proton, a deutron and an $$\alpha$$-particle with same kinetic energy enter into a uniform magnetic field at right angle to magnetic field. The ratio of the radii of their respective circular paths is :
Given below are two statements : One is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : In an uniform magnetic field, speed and energy remains the same for a moving charged particle.
Reason (R) : Moving charged particle experiences magnetic force perpendicular to its direction of motion.
The magnetic field at the centre of a circular coil of radius r, due to current I flowing through it, is B. The magnetic field at a point along the axis at a distance $${r \over 2}$$ from the centre is :
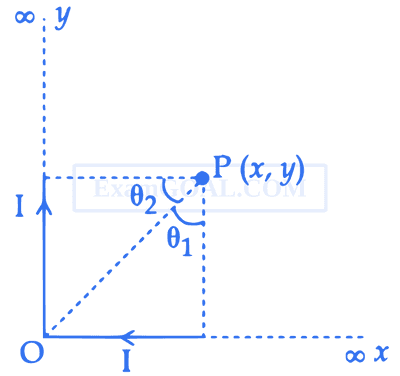
(Assume that the current is flowing in the clockwise direction.)
The ratio of the radii of trajectory of proton to that of $$\alpha$$-particle is 2 : 1. The ratio of Kp : K$$\alpha$$ is :
with velocity $$\left( {2\widehat i + 3\widehat j + 4\widehat k} \right)$$ ms–1. If an external
magnetic field of $$\left( {5\widehat i + 3\widehat j - 6\widehat k} \right)$$× 10–3 T exists in the region where the particle is moving then the
force on the particle is $$\overrightarrow F $$ × 10–9 N. The vector $$\overrightarrow F $$ is :
(mass of proton = 1.67 $$ \times $$ 10–27 kg, charge of the proton = 1.6 $$ \times $$ 10–19 C)
(Mass of the proton = 1.67 $$ \times $$ 10–27 kg, charge
of the proton = 1.69 $$ \times $$ 10–19 C)
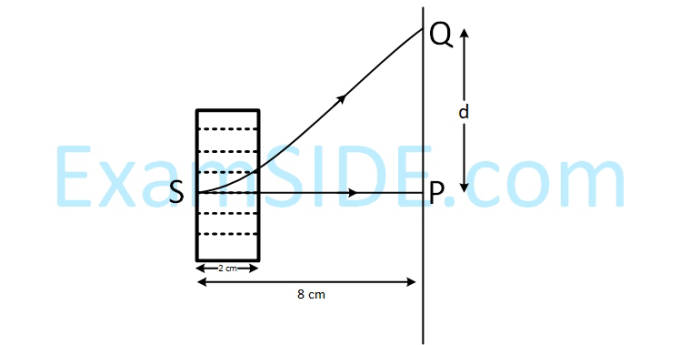
(Trajectory shown is schematic and not to scale) :

(A) E = $${3 \over 4}\left( {{{m{v^2}} \over {qa}}} \right)$$
(B) Rate of work done by the electric field at P is $${3 \over 4}\left( {{{m{v^3}} \over a}} \right)$$
(C) Rate of work done by both the fields at Q is zero
(D) The difference between the magnitude of angular momentum of the particle at P and Q is 2mav.
[Take $$\mu $$0 = 4$$\pi $$ × 10–7 NA–2]
$$\overrightarrow E = 2\widehat i + 3\widehat j;\,\,\,\overrightarrow B = 4\widehat j + 6\widehat k.$$
The charged particle is shifted from he origin to the point P(x = 1; y = 1) along a straight path. The magnitude of the total work done is :


($$g=$$ $$gravitational$$ $$acceleration$$ )

A rectangular loop of sides $$10$$ $$cm$$ and $$5$$ $$cm$$ carrying a current $$1$$ of $$12A$$ is placed in different orientations as shown in the figures below :
If there is a uniform magnetic field of $$0.3$$ $$T$$ in the positive $$z$$ direction, in which orientations the loop would be in $$(i)$$ stable equilibrium and $$(ii)$$ unstable equilibrium ?

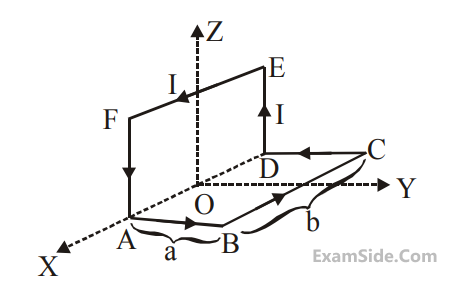
Due to the presence of the current $${I_1}$$ at the origin:

The magnitude of the magnetic field $$(B)$$ due to the loop $$ABCD$$ at the origin $$(O)$$ is :
$$\left( {{\mu _0} = 4\pi \times {{10}^{ - 7}}\,\,Tm\,\,{A^{ - 1}}} \right)$$
$$\left( {\mu = 4\pi \times {{10}^{ - 7}}Wb/A.m} \right)$$
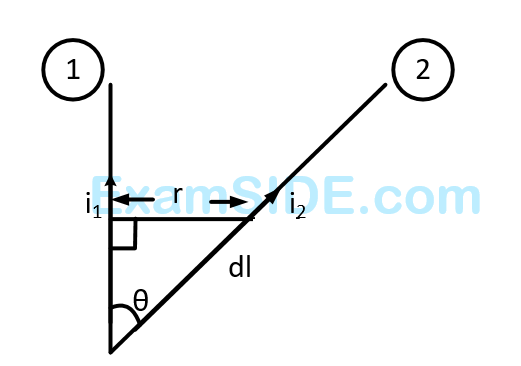
Numerical
If an optical medium possesses a relative permeability of $\frac{10}{\pi}$ and relative permittivity of $\frac{1}{0.0885}$, then the velocity of light is greater in vacuum than that in this medium by _________ times.
$$\left(\mu_0=4 \pi \times 10^{-7} \mathrm{H} / \mathrm{m}, \epsilon_0=8.85 \times 10^{-12} \mathrm{~F} / \mathrm{m}, \mathrm{c}=3 \times 10^8 \mathrm{~m} / \mathrm{s}\right)$$
A loop ABCDA , carrying current $\mathrm{I}=12 \mathrm{~A}$, is placed in a plane, consists of two semi-circular segments of radius $R_1=6 \pi \mathrm{~m}$ and $\mathrm{R}_2=4 \pi \mathrm{~m}$. The magnitude of the resultant magnetic field at center O is $\mathrm{k} \times 10^{-7} \mathrm{~T}$. The value of k is_________.
( Given $\mu_0=4 \pi \times 10^{-7} \mathrm{Tm} \mathrm{A}^{-1}$ )

A tightly wound long solenoid carries a current of 1.5 A . An electron is executing uniform circular motion inside the solenoid with a time period of 75 ns . The number of turns per metre in the solenoid is _________.
[Take mass of electron $\mathrm{m}_{\mathrm{e}}=9 \times 10^{-31} \mathrm{~kg}$, charge of electron $\left|\mathrm{q}_{\mathrm{e}}\right|=1.6 \times 10^{-19} \mathrm{C}$, $$ \left.\mu_0=4 \pi \times 10^{-7} \frac{\mathrm{~N}}{\mathrm{~A}^2}, 1 \mathrm{~ns}=10^{-9} \mathrm{~s}\right] $$
A current of 5 A exists in a square loop of side $\frac{1}{\sqrt{2}} \mathrm{~m}$. Then the magnitude of the magnetic field $B$ at the centre of the square loop will be $p \times 10^{-6} \mathrm{~T}$. where, value of p is ________ $\left[\right.$ Take $\mu_0=4 \pi \times 10^{-7} \mathrm{~T} \mathrm{~mA}^{-1}$ ].
A proton is moving undeflected in a region of crossed electric and magnetic fields at a constant speed of $2 \times 10^5 \mathrm{~ms}^{-1}$. When the electric field is switched off, the proton moves along a circular path of radius 2 cm . The magnitude of electric field is $x \times 10^4 \mathrm{~N} / \mathrm{C}$. The value of $x$ is _________. Take the mass of the proton $=1.6 \times 10^{-27} \mathrm{~kg}$.
Two long parallel wires $X$ and $Y$, separated by a distance of 6 cm , carry currents of 5 A and 4A, respectively, in opposite directions as shown in the figure. Magnitude of the resultant magnetic field at point P at a distance of 4 cm from wire Y is $x \times 10^{-5} \mathrm{~T}$. The value of $x$ is _________ . Take permeability of free space as $\mu_0=4 \pi \times 10^{-7}$ SI units.

A straight magnetic strip has a magnetic moment of $$44 \mathrm{~Am}^2$$. If the strip is bent in a semicircular shape, its magnetic moment will be ________ $$\mathrm{Am}^2$$.
(given $$\pi=\frac{22}{7}$$)
A square loop of edge length $$2 \mathrm{~m}$$ carrying current of $$2 \mathrm{~A}$$ is placed with its edges parallel to the $$x$$-$$y$$ axis. A magnetic field is passing through the $$x$$-$$y$$ plane and expressed as $$\vec{B}=B_0(1+4 x) \hat{k}$$, where $$B_o=5 T$$. The net magnetic force experienced by the loop is _________ $$\mathrm{N}$$.
A square loop PQRS having 10 turns, area $$3.6 \times 10^{-3} \mathrm{~m}^2$$ and resistance $$100 \Omega$$ is slowly and uniformly being pulled out of a uniform magnetic field of magnitude $$\mathrm{B}=0.5 \mathrm{~T}$$ as shown. Work done in pulling the loop out of the field in $$1.0 \mathrm{~s}$$ is _________ $$\times 10^{-6} \mathrm{~J}$$.

An electron with kinetic energy $$5 \mathrm{~eV}$$ enters a region of uniform magnetic field of 3 $$\mu \mathrm{T}$$ perpendicular to its direction. An electric field $$\mathrm{E}$$ is applied perpendicular to the direction of velocity and magnetic field. The value of E, so that electron moves along the same path, is __________ $$\mathrm{NC}^{-1}$$.
(Given, mass of electron $$=9 \times 10^{-31} \mathrm{~kg}$$, electric charge $$=1.6 \times 10^{-19} \mathrm{C}$$)
A coil having 100 turns, area of $$5 \times 10^{-3} \mathrm{~m}^2$$, carrying current of $$1 \mathrm{~mA}$$ is placed in uniform magnetic field of $$0.20 \mathrm{~T}$$ such a way that plane of coil is perpendicular to the magnetic field. The work done in turning the coil through $$90^{\circ}$$ is _________ $$\mu \mathrm{J}$$.
A circular coil having 200 turns, $$2.5 \times 10^{-4} \mathrm{~m}^2$$ area and carrying $$100 \mu \mathrm{A}$$ current is placed in a uniform magnetic field of $$1 \mathrm{~T}$$. Initially the magnetic dipole moment $$(\vec{M})$$ was directed along $$\vec{B}$$. Amount of work, required to rotate the coil through $$90^{\circ}$$ from its initial orientation such that $$\vec{M}$$ becomes perpendicular to $$\vec{B}$$, is ________ $$\mu$$J.
A solenoid of length $$0.5 \mathrm{~m}$$ has a radius of $$1 \mathrm{~cm}$$ and is made up of '$$\mathrm{m}$$' number of turns. It carries a current of $$5 \mathrm{~A}$$. If the magnitude of the magnetic field inside the solenoid is $$6.28 \times 10^{-3} \mathrm{~T}$$ then the value of $$\mathrm{m}$$ is __________.
A 2A current carrying straight metal wire of resistance $$1 \Omega$$, resistivity $$2 \times 10^{-6} \Omega \mathrm{m}$$, area of cross-section $$10 \mathrm{~mm}^2$$ and mass $$500 \mathrm{~g}$$ is suspended horizontally in mid air by applying a uniform magnetic field $$\vec{B}$$. The magnitude of B is ________ $$\times 10^{-1} \mathrm{~T}$$ (given, $$\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$$).
Two parallel long current carrying wire separated by a distance $$2 r$$ are shown in the figure. The ratio of magnetic field at $$A$$ to the magnetic field produced at $$C$$ is $$\frac{x}{7}$$. The value of $$x$$ is __________.

A rod of length $$60 \mathrm{~cm}$$ rotates with a uniform angular velocity $$20 \mathrm{~rad} \mathrm{s}^{-1}$$ about its perpendicular bisector, in a uniform magnetic filed $$0.5 T$$. The direction of magnetic field is parallel to the axis of rotation. The potential difference between the two ends of the rod is _________ V.
The magnetic field existing in a region is given by $$\vec{B}=0.2(1+2 x) \hat{k}$$. A square loop of edge $$50 \mathrm{~cm}$$ carrying 0.5 A current is placed in $$x$$-$$y$$ plane with its edges parallel to the $$x$$-$$y$$ axes, as shown in figure. The magnitude of the net magnetic force experienced by the loop is _________ $$\mathrm{mN}$$.

If an electric current of $4 \pi \sqrt{3}$ A is flowing through the sides of the polygon, the magnetic field at the centre of the polygon would be $x \times 10^{-7} \mathrm{~T}$.
The value of $x$ is _________.
Two circular coils $$P$$ and $$Q$$ of 100 turns each have same radius of $$\pi \mathrm{~cm}$$. The currents in $$P$$ and $$R$$ are $$1 A$$ and $$2 A$$ respectively. $$P$$ and $$Q$$ are placed with their planes mutually perpendicular with their centers coincide. The resultant magnetic field induction at the center of the coils is $$\sqrt{x} ~m T$$, where $$x=$$ __________.
[Use $$\mu_0=4 \pi \times 10^{-7} \mathrm{~TmA}^{-1}$$]
An electron moves through a uniform magnetic field $$\vec{B}=B_0 \hat{i}+2 B_0 \hat{j} T$$. At a particular instant of time, the velocity of electron is $$\vec{u}=3 \hat{i}+5 \hat{j} \mathrm{~m} / \mathrm{s}$$. If the magnetic force acting on electron is $$\vec{F}=5 e \hat{k} N$$, where $$e$$ is the charge of electron, then the value of $$B_0$$ is _________ $$T$$.
The current of $$5 \mathrm{~A}$$ flows in a square loop of sides $$1 \mathrm{~m}$$ is placed in air. The magnetic field at the centre of the loop is $$X \sqrt{2} \times 10^{-7} T$$. The value of $$X$$ is _________.
A charge of $$4.0 \mu \mathrm{C}$$ is moving with a velocity of $$4.0 \times 10^6 \mathrm{~ms}^{-1}$$ along the positive $$y$$ axis under a magnetic field $$\vec{B}$$ of strength $$(2 \hat{k}) \mathrm{T}$$. The force acting on the charge is $$x \hat{i} N$$. The value of $$x$$ is __________.
The magnetic field at the centre of a wire loop formed by two semicircular wires of radii $$R_1=2 \pi \mathrm{m}$$ and $$R_2=4 \pi \mathrm{m}$$, carrying current $$\mathrm{I}=4 \mathrm{~A}$$ as per figure given below is $$\alpha \times 10^{-7} \mathrm{~T}$$. The value of $$\alpha$$ is ________. (Centre $$\mathrm{O}$$ is common for all segments)

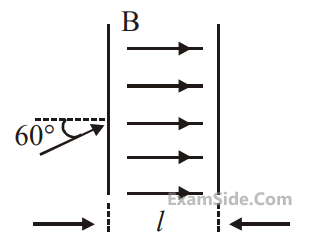
Two long, straight wires carry equal currents in opposite directions as shown in figure. The separation between the wires is $$5.0 \mathrm{~cm}$$. The magnitude of the magnetic field at a point $$\mathrm{P}$$ midway between the wires is _______ $$\mu \mathrm{T}$$
(Given : $$\mu_0=4 \pi \times 10^{-7} \mathrm{TmA}^{-1}$$)

A straight wire $$\mathrm{AB}$$ of mass $$40 \mathrm{~g}$$ and length $$50 \mathrm{~cm}$$ is suspended by a pair of flexible leads in uniform magnetic field of magnitude $$0.40 \mathrm{~T}$$ as shown in the figure. The magnitude of the current required in the wire to remove the tension in the supporting leads is ___________ A.
$$\left(\right.$$ Take $$g=10 \mathrm{~ms}^{-2}$$ ).

A straight wire carrying a current of $$14 \mathrm{~A}$$ is bent into a semi-circular arc of radius $$2.2 \mathrm{~cm}$$ as shown in the figure. The magnetic field produced by the current at the centre $$(\mathrm{O})$$ of the arc. is ____________ $$\times ~10^{-4} \mathrm{~T}$$

The ratio of magnetic field at the centre of a current carrying coil of radius $$r$$ to the magnetic field at distance $$r$$ from the centre of coil on its axis is $$\sqrt{x}: 1$$. The value of $$x$$ is __________
A proton with a kinetic energy of $$2.0 ~\mathrm{eV}$$ moves into a region of uniform magnetic field of magnitude $$\frac{\pi}{2} \times 10^{-3} \mathrm{~T}$$. The angle between the direction of magnetic field and velocity of proton is $$60^{\circ}$$. The pitch of the helical path taken by the proton is __________ $$\mathrm{cm}$$. (Take, mass of proton $$=1.6 \times 10^{-27} \mathrm{~kg}$$ and Charge on proton $$=1.6 \times 10^{-19} \mathrm{C}$$ ).
Two identical circular wires of radius $$20 \mathrm{~cm}$$ and carrying current $$\sqrt{2} \mathrm{~A}$$ are placed in perpendicular planes as shown in figure. The net magnetic field at the centre of the circular wires is __________ $$\times 10^{-8} \mathrm{~T}$$.

(Take $$\pi=3.14$$)
A charge particle of $$2 ~\mu \mathrm{C}$$ accelerated by a potential difference of $$100 \mathrm{~V}$$ enters a region of uniform magnetic field of magnitude $$4 ~\mathrm{mT}$$ at right angle to the direction of field. The charge particle completes semicircle of radius $$3 \mathrm{~cm}$$ inside magnetic field. The mass of the charge particle is __________ $$\times 10^{-18} \mathrm{~kg}$$
Two long parallel wires carrying currents 8A and 15A in opposite directions are placed at a distance of 7 cm from each other. A point P is at equidistant from both the wires such that the lines joining the point P to the wires are perpendicular to each other. The magnitude of magnetic field at P is _____________ $$\times~10^{-6}$$ T.
(Given : $$\sqrt2=1.4$$)
A single turn current loop in the shape of a right angle triangle with sides 5 cm, 12 cm, 13 cm is carrying a current of 2 A. The loop is in a uniform magnetic field of magnitude 0.75 T whose direction is parallel to the current in the 13 cm side of the loop. The magnitude of the magnetic force on the 5 cm side will be $$\frac{x}{130}$$ N. The value of $$x$$ is ____________.
A closely wounded circular coil of radius 5 cm produces a magnetic field of $$37.68 \times 10^{-4} \mathrm{~T}$$ at its center. The current through the coil is _________A.
[Given, number of turns in the coil is 100 and $$\pi=3.14$$]
A wire of length $$314 \mathrm{~cm}$$ carrying current of $$14 \mathrm{~A}$$ is bent to form a circle. The magnetic moment of the coil is ________ A $$-\mathrm{m}^{2}$$. [Given $$\pi=3.14$$]
A singly ionized magnesium atom (A = 24) ion is accelerated to kinetic energy 5 keV, and is projected perpendicularly into a magnetic field B of the magnitude 0.5 T. The radius of path formed will be _____________ cm.
A deuteron and a proton moving with equal kinetic energy enter into a uniform magnetic field at right angle to the field. If rd and rp are the radii of their circular paths respectively, then the ratio $${{{r_d}} \over {{r_p}}}$$ will be $$\sqrt{x}$$ : 1 where x is __________.
Two 10 cm long, straight wires, each carrying a current of 5A are kept parallel to each other. If each wire experienced a force of 10$$-$$5 N, then separation between the wires is ____________ cm.