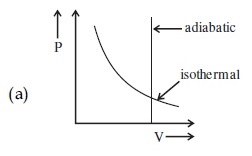
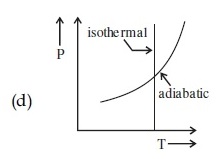
Heat and Thermodynamics · Physics · JEE Main
MCQ (Single Correct Answer)
A monoatomic gas having $ \gamma = \frac{5}{3} $ is stored in a thermally insulated container and the gas is suddenly compressed to $ \left( \frac{1}{8} \right)^{\text{th}} $ of its initial volume. The ratio of final pressure and initial pressure is:
($\gamma$ is the ratio of specific heats of the gas at constant pressure and at constant volume)
Water falls from a height of 200 m into a pool. Calculate the rise in temperature of the water assuming no heat dissipation from the water in the pool.
(Take g = 10 m/s2, specific heat of water = 4200 J/(kg K))
The helium and argon are put in the flask at the same room temperature (300 K). The ratio of average kinetic energies (per molecule) of helium and argon is:
(Give: Molar mass of helium = 4 g/mol, Molar mass of argon = 40 g/mol)
Match List - I with List - II.
| List - I | List - II |
|---|---|
| (A) Isothermal | (I) ΔW (work done) = 0 |
| (B) Adiabatic | (II) ΔQ (supplied heat) = 0 |
| (C) Isobaric | (III) ΔU (change in internal energy) ≠ 0 |
| (D) Isochoric | (IV) ΔU = 0 |
Choose the correct answer from the options given below :
Match the List I with List II
| List - I | List - II | ||
|---|---|---|---|
| (A) | Triatomic rigid gas | (I) | $\frac{C_p}{C_v}=\frac{5}{3}$ |
| (B) | Diatomic non-rigid gas | (II) | $\frac{C_p}{C_v}=\frac{7}{5}$ |
| (C) | Monoatomic gas | (III) | $\frac{C_p}{C_v}=\frac{4}{3}$ |
| (D) | Diatomic rigid gas | (IV) | $\frac{C_p}{C_v}=\frac{9}{7}$ |
Choose the correct answer from the options given below:
Consider a rectangular sheet of solid material of length $l=9 \mathrm{~cm}$ and width $\mathrm{d}=4 \mathrm{~cm}$. The coefficient of linear expansion is $\alpha=3.1 \times 10^{-5} \mathrm{~K}^{-1}$ at room temperature and one atmospheric pressure. The mass of sheet $m=0.1 \mathrm{~kg}$ and the specific heat capacity $C_{\mathrm{v}}=900 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}$. If the amount of heat supplied to the material is $8.1 \times 10^2 \mathrm{~J}$ then change in area of the rectangular sheet is :
There are two vessels filled with an ideal gas where volume of one is double the volume of other. The large vessel contains the gas at 8 kPa at 1000 K while the smaller vessel contains the gas at 7 kPa at 500 K . If the vessels are connected to each other by a thin tube allowing the gas to flow and the temperature of both vessels is maintained at 600 K , at steady state the pressure in the vessels will be (in kPa ).
Match List - I with List - II.
| List - I | List - II |
||
|---|---|---|---|
| (A) | Isobaric | (I) | $\Delta Q=\Delta W$ |
| (B) | Isochoric | (II) | $\Delta Q=\Delta U$ |
| (C) | Adiabatic | (III) | $\Delta Q=$ zero |
| (D) | Isothermal | (IV) | $\Delta Q=\Delta U+P\Delta V$ |
$\Delta Q=$ Heat supplied
$\Delta W=$ Work done by the system
$\Delta \mathrm{U}=$ Change in internal energy
$\mathrm{P}=$ Pressure of the system
$\Delta \mathrm{V}=$ Change in volume of the system
Choose the correct answer from the options given below :
Consider the sound wave travelling in ideal gases of $\mathrm{He}, \mathrm{CH}_4$, and $\mathrm{CO}_2$. All the gases have the same ratio $\frac{P}{\rho}$, where $P$ is the pressure and $\rho$ is the density. The ratio of the speed of sound through the gases $\mathrm{V}_{\mathrm{He}}: \mathrm{V}_{\mathrm{CH}_4}: \mathrm{V}_{\mathrm{CO}_2}$ is given by
The mean free path and the average speed of oxygen molecules at 300 K and 1 atm are $3 \times 10^{-7} \mathrm{~m}$ and $600 \mathrm{~m} / \mathrm{s}$, respectively. Find the frequency of its collisions.
A gas is kept in a container having walls which are thermally non-conducting. Initially the gas has a volume of $800 \mathrm{~cm}^3$ and temperature $27^{\circ} \mathrm{C}$. The change in temperature when the gas is adiabatically compressed to $200 \mathrm{~cm}^3$ is:
(Take $\gamma=1.5 ; \gamma$ is the ratio of specific heats at constant pressure and at constant volume)

A piston of mass $M$ is hung from a massless spring whose restoring force law goes as $F=-k x^3$, where k is the spring constant of appropriate dimension. The piston separates the vertical chamber into two parts, where the bottom part is filled with ' $n$ ' moles of an ideal gas. An external work is done on the gas isothermally (at a constant temperature T) with the help of a heating filament (with negligible volume) mounted in lower part of the chamber, so that the piston goes up from a height $\mathrm{L}_0$ to $\mathrm{L}_1$, the total energy delivered by the filament is:(Assume spring to be in its natural length before heating)
$$ \begin{array}{lll} & \text { List - I } & {List - II }\\ \text { } \\ \text { (A) } & \text { Heat capacity of body } & \text { (I) } \mathrm{J} \mathrm{~kg}^{-1} \\ \text { (B) } & \text { Specific heat capacity of body } & \text { (II) } \mathrm{J} \mathrm{~K}^{-1} \\ \text { (C) } & \text { Latent heat } & \text { (III) } \mathrm{J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1} \\ \text { (D) } & \text { Thermal conductivity } & \text { (IV) } \mathrm{J} \mathrm{~m}^{-1} \mathrm{~K}^{-1} \mathrm{~s}^{-1} \end{array} $$
$$ \text { Choose the correct answer from the options given below : } $$In an adiabatic process, which of the following statements is true?
The equation for real gas is given by $\left(\mathrm{P}+\frac{\mathrm{a}}{\mathrm{V}^2}\right)(\mathrm{V}-\mathrm{b})=\mathrm{RT}$, where $\mathrm{P}, \mathrm{V}, \mathrm{T}$ and R are the pressure, volume, temperature and gas constant, respectively. The dimension of $\mathrm{ab}^{-2}$ is equivalent to that of :
The difference of temperature in a material can convert heat energy into electrical energy. To harvest the heat energy, the material should have
Given below are two statements. One is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : With the increase in the pressure of an ideal gas, the volume falls off more rapidly in an isothermal process in comparison to the adiabatic process.
Reason (R) : In isothermal process, PV = constant, while in adiabatic process $PV^{\gamma}$ = constant. Here $\gamma$ is the ratio of specific heats, P is the pressure and V is the volume of the ideal gas.
In the light of the above statements, choose the correct answer from the options given below:
A cup of coffee cools from 90°C to 80°C in t minutes when the room temperature is 20°C. The time taken by the similar cup of coffee to cool from 80°C to 60°C at the same room temperature is:

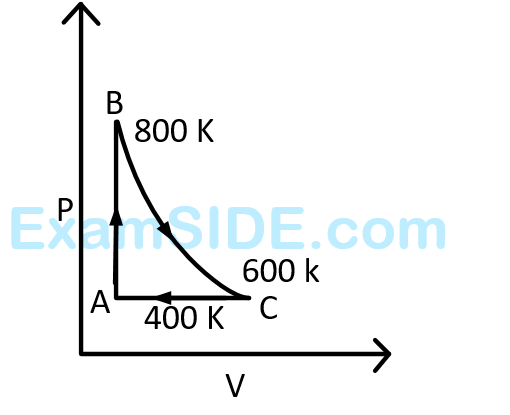
A poly-atomic molecule $\left(C_V=3 R, C_P=4 R\right.$, where $R$ is gas constant) goes from phase space point $\mathrm{A}\left(\mathrm{P}_{\mathrm{A}}=10^5 \mathrm{~Pa}, \mathrm{~V}_{\mathrm{A}}=4 \times 10^{-6} \mathrm{~m}^3\right)$ to point $\mathrm{B}\left(\mathrm{P}_{\mathrm{B}}=5 \times 10^4 \mathrm{~Pa}, \mathrm{~V}_{\mathrm{B}}=6 \times 10^{-6} \mathrm{~m}^3\right)$ to point $\mathrm{C}\left(\mathrm{P}_{\mathrm{C}}=10^4\right.$ $\mathrm{Pa}, \mathrm{V}_C=8 \times 10^{-6} \mathrm{~m}^3$ ). A to $B$ is an adiabatic path and $B$ to $C$ is an isothermal path.
The net heat absorbed per unit mole by the system is :
The work done in an adiabatic change in an ideal gas depends upon only :
The ratio of vapour densities of two gases at the same temperature is $ \frac{4}{25} $, then the ratio of r.m.s. velocities will be :
The kinetic energy of translation of the molecules in 50 g of $ \text{CO}_2 $ gas at 17°C is :
For a particular ideal gas which of the following graphs represents the variation of mean squared velocity of the gas molecules with temperature?
A Carnot engine $(\mathrm{E})$ is working between two temperatures 473 K and 273 K . In a new system two engines - engine $E_1$ works between 473 K to 373 K and engine $E_2$ works between 373 K to 273 K . If $\eta_{12}, \eta_1$ and $\eta_2$ are the efficiencies of the engines $E, E_1$ and $E_2$, respectively, then
The temperature of a body in air falls from $40^{\circ} \mathrm{C}$ to $24^{\circ} \mathrm{C}$ in 4 minutes. The temperature of the air is $16^{\circ} \mathrm{C}$. The temperature of the body in the next 4 minutes will be :
The magnitude of heat exchanged by a system for the given cyclic process ABCA (as shown in figure) is (in SI unit) :

Given below are two statements. One is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : In an insulated container, a gas is adiabatically shrunk to half of its initial volume. The temperature of the gas decreases.
Reason (R) : Free expansion of an ideal gas is an irreversible and an adiabatic process.
In the light of the above statements, choose the correct answer from the options given below :
Which of the following figure represents the relation between Celsius and Fahrenheit temperatures?
An ideal gas goes from an initial state to final state. During the process, the pressure of gas increases linearly with temperature.
A. The work done by gas during the process is zero.
B. The heat added to gas is different from change in its internal energy.
C. The volume of the gas is increased.
D. The internal energy of the gas is increased.
E. The process is isochoric (constant volume process)
Choose the correct answer from the options given below:
Water of mass $m$ gram is slowly heated to increase the temperature from $T_1$ to $T_\gamma$. The change in entropy of the water, given specific heat of water is $1 \mathrm{Jkg}^{-1} \mathrm{~K}^{-1}$, is :

Using the given $P-V$ diagram, the work done by an ideal gas along the path $A B C D$ is :
Match the List - I with List - II
| List - I | List - II | ||
|---|---|---|---|
| (A) | Pressure varies inversely with volume of an ideal gas. | (I) | Adiabatic process |
| (B) | Heat absorbed goes partly to increase internal energy and partly to do work. | (II) | Isochoric process |
| (C) | Heat is neither absorbed nor released by a system. | (III) | Isothermal process |
| (D) | No work is done on or by a gas. | (IV) | Isobaric process |
Choose the correct answer from the options given below:
A gun fires a lead bullet of temperature 300 K into a wooden block. The bullet having melting temperature of 600 K penetrates into the block and melts down. If the total heat required for the process is 625 J , then the mass of the bullet is _______ grams. (Latent heat of fusion of lead $=2.5 \times 10^4 \mathrm{JKg}^{-1}$ and specific heat capacity of lead $=125 \mathrm{JKg}^{-1}$ $\left.\mathrm{K}^{-1}\right)$
Given are statements for certain thermodynamic variables,
(A) Internal energy, volume $(\mathrm{V})$ and mass $(\mathrm{M})$ are extensive variables.
(B) Pressure (P), temperature ( T ) and density ( $\rho$ ) are intensive variables.
(C) Volume (V), temperature (T) and density ( $\rho$ ) are intensive variables.
(D) Mass (M), temperature (T) and internal energy are extensive variables.
Choose the correct answer from the options given below :
For a diatomic gas, if $\gamma_1=\left(\frac{C p}{C v}\right)$ for rigid molecules and $\gamma_2=\left(\frac{C p}{C v}\right)$ for another diatomic molecules, but also having vibrational modes. Then, which one of the following options is correct? (Cp and Cv are specific heats of the gas at constant pressure and volume)
Two spherical bodies of same materials having radii 0.2 m and 0.8 m are placed in same atmosphere. The temperature of the smaller body is 800 K and temperature of the bigger body is 400 K . If the energy radiated from the smaller body is E, the energy radiated from the bigger body is (assume, effect of the surrounding temperature to be negligible),
An amount of ice of mass $10^{-3} \mathrm{~kg}$ and temperature $-10^{\circ} \mathrm{C}$ is transformed to vapour of temperature $110^{\circ} \mathrm{C}$ by applying heat. The total amount of work required for this conversion is, (Take, specific heat of ice $=2100 \mathrm{Jkg}^{-1} \mathrm{~K}^{-1}$, specific heat of water $=4180 \mathrm{Jkg}^{-1} \mathrm{~K}^{-1}$, specific heat of steam $=1920 \mathrm{Jkg}^{-1} \mathrm{~K}^{-1}$, Latent heat of ice $=3.35 \times 10^5 \mathrm{Jkg}^{-1}$ and Latent heat of steam $=2.25 \times 10^6$ $\mathrm{Jkg}^{-1}$ )
A real gas within a closed chamber at $$27^{\circ} \mathrm{C}$$ undergoes the cyclic process as shown in figure. The gas obeys $$P V^3=R T$$ equation for the path $$A$$ to $$B$$. The net work done in the complete cycle is (assuming $$R=8 \mathrm{~J} / \mathrm{mol} \mathrm{K}$$):

The temperature of a gas is $$-78^{\circ} \mathrm{C}$$ and the average translational kinetic energy of its molecules is $$\mathrm{K}$$. The temperature at which the average translational kinetic energy of the molecules of the same gas becomes $$2 \mathrm{~K}$$ is :
The volume of an ideal gas $$(\gamma=1.5)$$ is changed adiabatically from 5 litres to 4 litres. The ratio of initial pressure to final pressure is :
A sample of 1 mole gas at temperature $$T$$ is adiabatically expanded to double its volume. If adiab constant for the gas is $$\gamma=\frac{3}{2}$$, then the work done by the gas in the process is :
A diatomic gas $$(\gamma=1.4)$$ does $$100 \mathrm{~J}$$ of work in an isobaric expansion. The heat given to the gas is :
Given below are two statements :
Statement (I) : The mean free path of gas molecules is inversely proportional to square of molecular diameter.
Statement (II) : Average kinetic energy of gas molecules is directly proportional to absolute temperature of gas.
In the light of the above statements, choose the correct answer from the options given below :
A mixture of one mole of monoatomic gas and one mole of a diatomic gas (rigid) are kept at room temperature $$(27^{\circ} \mathrm{C})$$. The ratio of specific heat of gases at constant volume respectively is:
Two different adiabatic paths for the same gas intersect two isothermal curves as shown in P-V diagram. The relation between the ratio $$\frac{V_a}{V_d}$$ and the ratio $$\frac{V_b}{V_c}$$ is:

Given below are two statements:
Statement (I) : Dimensions of specific heat is $$[\mathrm{L}^2 \mathrm{~T}^{-2} \mathrm{~K}^{-1}]$$.
Statement (II) : Dimensions of gas constant is $$[\mathrm{M} \mathrm{L}^2 \mathrm{~T}^{-1} \mathrm{~K}^{-1}]$$.
In the light of the above statements, choose the most appropriate answer from the options given below.
Energy of 10 non rigid diatomic molecules at temperature $$\mathrm{T}$$ is :
A total of $$48 \mathrm{~J}$$ heat is given to one mole of helium kept in a cylinder. The temperature of helium increases by $$2^{\circ} \mathrm{C}$$. The work done by the gas is: Given, $$\mathrm{R}=8.3 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}$$.
The specific heat at constant pressure of a real gas obeying $$P V^2=R T$$ equation is:
A sample contains mixture of helium and oxygen gas. The ratio of root mean square speed of helium and oxygen in the sample, is :
During an adiabatic process, if the pressure of a gas is found to be proportional to the cube of its absolute temperature, then the ratio of $$\frac{\mathrm{C}_{\mathrm{P}}}{\mathrm{C}_{\mathrm{V}}}$$ for the gas is :
If $$\mathrm{n}$$ is the number density and $$\mathrm{d}$$ is the diameter of the molecule, then the average distance covered by a molecule between two successive collisions (i.e. mean free path) is represented by :
The heat absorbed by a system in going through the given cyclic process is :

If the collision frequency of hydrogen molecules in a closed chamber at $$27^{\circ} \mathrm{C}$$ is $$\mathrm{Z}$$, then the collision frequency of the same system at $$127^{\circ} \mathrm{C}$$ is :
A sample of gas at temperature $$T$$ is adiabatically expanded to double its volume. Adiabatic constant for the gas is $$\gamma=3 / 2$$. The work done by the gas in the process is:
$$(\mu=1 \text { mole })$$
The translational degrees of freedom $$\left(f_t\right)$$ and rotational degrees of freedom $$\left(f_r\right)$$ of $$\mathrm{CH}_4$$ molecule are:
P-T diagram of an ideal gas having three different densities $$\rho_1, \rho_2, \rho_3$$ (in three different cases) is shown in the figure. Which of the following is correct :

The resistances of the platinum wire of a platinum resistance thermometer at the ice point and steam point are $$8 \Omega$$ and $$10 \Omega$$ respectively. After inserting in a hot bath of temperature $$400^{\circ} \mathrm{C}$$, the resistance of platinum wire is :
On celcius scale the temperature of body increases by $$40^{\circ} \mathrm{C}$$. The increase in temperature on Fahrenheit scale is :
The speed of sound in oxygen at S.T.P. will be approximately: (given, $$R=8.3 \mathrm{~JK}^{-1}, \gamma=1.4$$)
A gas mixture consists of 8 moles of argon and 6 moles of oxygen at temperature T. Neglecting all vibrational modes, the total internal energy of the system is:
The given figure represents two isobaric processes for the same mass of an ideal gas, then

The parameter that remains the same for molecules of all gases at a given temperature is :
A block of ice at $$-10^{\circ} \mathrm{C}$$ is slowly heated and converted to steam at $$100^{\circ} \mathrm{C}$$. Which of the following curves represent the phenomenon qualitatively:
If three moles of monoatomic gas $$\left(\gamma=\frac{5}{3}\right)$$ is mixed with two moles of a diatomic gas $$\left(\gamma=\frac{7}{5}\right)$$, the value of adiabatic exponent $$\gamma$$ for the mixture is
Two thermodynamical processes are shown in the figure. The molar heat capacity for process A and B are $$\mathrm{C}_{\mathrm{A}}$$ and $$\mathrm{C}_{\mathrm{B}}$$. The molar heat capacity at constant pressure and constant volume are represented by $$\mathrm{C_P}$$ and $$\mathrm{C_V}$$, respectively. Choose the correct statement.

At which temperature the r.m.s. velocity of a hydrogen molecule equal to that of an oxygen molecule at $$47^{\circ} \mathrm{C}$$ ?
The temperature of a gas having $$2.0 \times 10^{25}$$ molecules per cubic meter at $$1.38 \mathrm{~atm}$$ (Given, $$\mathrm{k}=1.38 \times 10^{-23} \mathrm{JK}^{-1}$$) is :
$$N$$ moles of a polyatomic gas $$(f=6)$$ must be mixed with two moles of a monoatomic gas so that the mixture behaves as a diatomic gas. The value of $$N$$ is :
A thermodynamic system is taken from an original state $$\mathrm{A}$$ to an intermediate state $$B$$ by a linear process as shown in the figure. It's volume is then reduced to the original value from $$\mathrm{B}$$ to $$\mathrm{C}$$ by an isobaric process. The total work done by the gas from $$A$$ to $$B$$ and $$B$$ to $$C$$ would be :

Two vessels $$A$$ and $$B$$ are of the same size and are at same temperature. A contains $$1 \mathrm{~g}$$ of hydrogen and $$B$$ contains $$1 \mathrm{~g}$$ of oxygen. $$\mathrm{P}_{\mathrm{A}}$$ and $$\mathrm{P}_{\mathrm{B}}$$ are the pressures of the gases in $$\mathrm{A}$$ and $$\mathrm{B}$$ respectively, then $$\frac{P_A}{P_B}$$ is:
During an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio of $$\frac{\mathrm{Cp}}{\mathrm{Cv}}$$ for the gas is :
The equation of state of a real gas is given by $$\left(\mathrm{P}+\frac{\mathrm{a}}{\mathrm{V}^2}\right)(\mathrm{V}-\mathrm{b})=\mathrm{RT}$$, where $$\mathrm{P}, \mathrm{V}$$ and $$\mathrm{T}$$ are pressure, volume and temperature respectively and $$\mathrm{R}$$ is the universal gas constant. The dimensions of $$\frac{\mathrm{a}}{\mathrm{b}^2}$$ is similar to that of :
The total kinetic energy of 1 mole of oxygen at $$27^{\circ} \mathrm{C}$$ is : [Use universal gas constant $$(R)=8.31 \mathrm{~J} /$$ mole K]
$$0.08 \mathrm{~kg}$$ air is heated at constant volume through $$5^{\circ} \mathrm{C}$$. The specific heat of air at constant volume is $$0.17 \mathrm{~kcal} / \mathrm{kg}^{\circ} \mathrm{C}$$ and $$\mathrm{J}=4.18$$ joule/$$\mathrm{~cal}$$. The change in its internal energy is approximately.
The average kinetic energy of a monatomic molecule is $$0.414 \mathrm{~eV}$$ at temperature :
(Use $$K_B=1.38 \times 10^{-23} \mathrm{~J} / \mathrm{mol}-\mathrm{K}$$)

(Given: Atomic Weight of $\mathrm{Ar}=39.9$ )
The initial pressure and volume of an ideal gas are P$$_0$$ and V$$_0$$. The final pressure of the gas when the gas is suddenly compressed to volume $$\frac{V_0}{4}$$ will be :
(Given $$\gamma$$ = ratio of specific heats at constant pressure and at constant volume)
The mean free path of molecules of a certain gas at STP is $$1500 \mathrm{~d}$$, where $$\mathrm{d}$$ is the diameter of the gas molecules. While maintaining the standard pressure, the mean free path of the molecules at $$373 \mathrm{~K}$$ is approximately:
The rms speed of oxygen molecule in a vessel at particular temperature is $$\left(1+\frac{5}{x}\right)^{\frac{1}{2}} v$$, where $$v$$ is the average speed of the molecule. The value of $$x$$ will be:
$$\left(\right.$$ Take $$\left.\pi=\frac{22}{7}\right)$$
An engine operating between the boiling and freezing points of water will have
A. efficiency more than 27%.
B. efficiency less than the efficiency of a Carnot engine operating between the same two temperatures.
C. efficiency equal to $$27 \%$$
D. efficiency less than $$27 \%$$
Choose the correct answer from the options given below:
If the r. m.s speed of chlorine molecule is $$490 \mathrm{~m} / \mathrm{s}$$ at $$27^{\circ} \mathrm{C}$$, the r. m. s speed of argon molecules at the same temperature will be (Atomic mass of argon $$=39.9 \mathrm{u}$$, molecular mass of chlorine $$=70.9 \mathrm{u}$$ )
The Thermodynamic process, in which internal energy of the system remains constant is
The root mean square speed of molecules of nitrogen gas at $$27^{\circ} \mathrm{C}$$ is approximately : (Given mass of a nitrogen molecule $$=4.6 \times 10^{-26} \mathrm{~kg}$$ and take Boltzmann constant $$\mathrm{k}_{\mathrm{B}}=1.4 \times 10^{-23} \mathrm{JK}^{-1}$$ )
$$1 \mathrm{~kg}$$ of water at $$100^{\circ} \mathrm{C}$$ is converted into steam at $$100^{\circ} \mathrm{C}$$ by boiling at atmospheric pressure. The volume of water changes from $$1.00 \times 10^{-3} \mathrm{~m}^{3}$$ as a liquid to $$1.671 \mathrm{~m}^{3}$$ as steam. The change in internal energy of the system during the process will be
(Given latent heat of vaporisaiton $$=2257 \mathrm{~kJ} / \mathrm{kg}$$, Atmospheric pressure = $$\left.1 \times 10^{5} \mathrm{~Pa}\right)$$
On a temperature scale '$$\mathrm{X}$$', the boiling point of water is $$65^{\circ} \mathrm{X}$$ and the freezing point is $$-15^{\circ} \mathrm{X}$$. Assume that the $$\mathrm{X}$$ scale is linear. The equivalent temperature corresponding to $$-95^{\circ} \mathrm{X}$$ on the Farenheit scale would be:
Three vessels of equal volume contain gases at the same temperature and pressure. The first vessel contains neon (monoatomic), the second contains chlorine (diatomic) and third contains uranium hexafloride (polyatomic). Arrange these on the basis of their root mean square speed $$\left(v_{\mathrm{rms}}\right)$$ and choose the correct answer from the options given below:
A gas mixture consists of 2 moles of oxygen and 4 moles of neon at temperature T. Neglecting all vibrational modes, the total internal energy of the system will be,
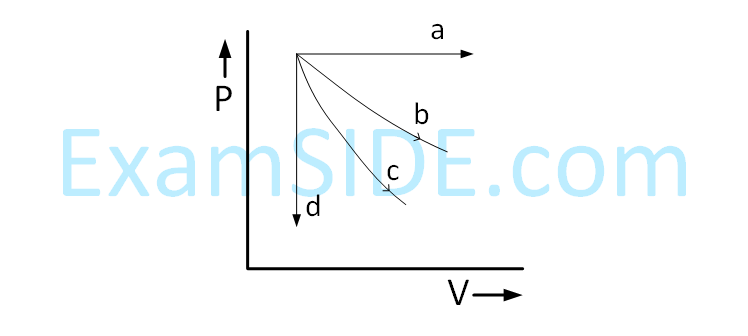
A gas is compressed adiabatically, which one of the following statement is NOT true.
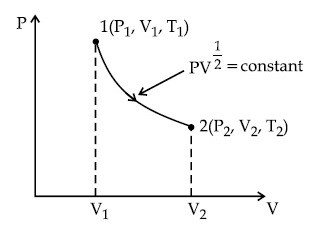
Consider two containers A and B containing monoatomic gases at the same Pressure (P), Volume (V) and Temperature (T). The gas in A is compressed isothermally to $$\frac{1}{8}$$ of its original volume while the gas in B is compressed adiabatically to $$\frac{1}{8}$$ of its original volume. The ratio of final pressure of gas in B to that of gas in A is
Match List I with List II :
| List I | List II | ||
|---|---|---|---|
| (A) | 3 Translational degrees of freedom | (I) | Monoatomic gases |
| (B) | 3 Translational, 2 rotational degrees of freedoms | (II) | Polyatomic gases |
| (C) | 3 Translational, 2 rotational and 1 vibrational degrees of freedom | (III) | Rigid diatomic gases |
| (D) | 3 Translational, 3 rotational and more than one vibrational degrees of freedom | (IV) | Nonrigid diatomic gases |
Choose the correct answer from the options given below:
The temperature at which the kinetic energy of oxygen molecules becomes double than its value at $$27^{\circ} \mathrm{C}$$ is
Work done by a Carnot engine operating between temperatures $$127^{\circ} \mathrm{C}$$ and $$27^{\circ} \mathrm{C}$$ is $$2 \mathrm{~kJ}$$. The amount of heat transferred to the engine by the reservoir is :
Given below are two statements:
Statement I: If heat is added to a system, its temperature must increase.
Statement II: If positive work is done by a system in a thermodynamic process, its volume must increase.
In the light of the above statements, choose the correct answer from the options given below
The temperature of an ideal gas is increased from $$200 \mathrm{~K}$$ to $$800 \mathrm{~K}$$. If r.m.s. speed of gas at $$200 \mathrm{~K}$$ is $$v_{0}$$. Then, r.m.s. speed of the gas at $$800 \mathrm{~K}$$ will be:
A body cools in 7 minutes from $$60^{\circ} \mathrm{C}$$ to $$40^{\circ} \mathrm{C}$$. The temperature of the surrounding is $$10^{\circ} \mathrm{C}$$. The temperature of the body after the next 7 minutes will be:
The ratio of speed of sound in hydrogen gas to the speed of sound in oxygen gas at the same temperature is:
A source supplies heat to a system at the rate of $$1000 \mathrm{~W}$$. If the system performs work at a rate of $$200 \mathrm{~W}$$. The rate at which internal energy of the system increases is
The number of air molecules per cm$$^3$$ increased from $$3\times10^{19}$$ to $$12\times10^{19}$$. The ratio of collision frequency of air molecules before and after the increase in number respectively is:
A Carnot engine operating between two reservoirs has efficiency $$\frac{1}{3}$$. When the temperature of cold reservoir raised by x, its efficiency decreases to $$\frac{1}{6}$$. The value of x, if the temperature of hot reservoir is $$99^\circ$$C, will be :
For three low density gases A, B, C pressure versus temperature graphs are plotted while keeping them at constant volume, as shown in the figure.

The temperature corresponding to the point '$$\mathrm{K}$$' is :
A sample of gas at temperature $$T$$ is adiabatically expanded to double its volume. The work done by the gas in the process is $$\left(\mathrm{given}, \gamma=\frac{3}{2}\right)$$ :
$$\left(P+\frac{a}{V^{2}}\right)(V-b)=R T$$ represents the equation of state of some gases. Where $$P$$ is the pressure, $$V$$ is the volume, $$T$$ is the temperature and $$a, b, R$$ are the constants. The physical quantity, which has dimensional formula as that of $$\frac{b^{2}}{a}$$, will be:
The average kinetic energy of a molecule of the gas is
The pressure of a gas changes linearly with volume from $$\mathrm{A}$$ to $$\mathrm{B}$$ as shown in figure. If no heat is supplied to or extracted from the gas then change in the internal energy of the gas will be

The correct relation between $$\gamma = {{{c_p}} \over {{c_v}}}$$ and temperature T is :
Assertion A: Efficiency of a reversible heat engine will be highest at $-273^{\circ} \mathrm{C}$ temperature of cold reservoir.
Reason R: The efficiency of Carnot's engine depends not only on the temperature of the cold reservoir but it depends on the temperature of the hot reservoir too and is given as $\eta=\left(1-\frac{T_{2}}{T_{1}}\right)$
In the light of the above statements, choose the correct answer from the options given below
The pressure $$(\mathrm{P})$$ and temperature ($$\mathrm{T})$$ relationship of an ideal gas obeys the equation $$\mathrm{PT}^{2}=$$ constant. The volume expansion coefficient of the gas will be :
Heat is given to an ideal gas in an isothermal process.
A. Internal energy of the gas will decrease.
B. Internal energy of the gas will increase.
C. Internal energy of the gas will not change.
D. The gas will do positive work.
E. The gas will do negative work.
Choose the correct answer from the options given below :
Heat energy of 184 kJ is given to ice of mass 600 g at $$-12^\circ \mathrm{C}$$. Specific heat of ice is $$\mathrm{2222.3~J~kg^{-1^\circ}~C^{-1}}$$ and latent heat of ice in 336 $$\mathrm{kJ/kg^{-1}}$$
A. Final temperature of system will be 0$$^\circ$$C.
B. Final temperature of the system will be greater than 0$$^\circ$$C.
C. The final system will have a mixture of ice and water in the ratio of 5 : 1.
D. The final system will have a mixture of ice and water in the ratio of 1 : 5.
E. The final system will have water only.
Choose the correct answer from the options given below :
At 300 K, the rms speed of oxygen molecules is $$\sqrt {{{\alpha + 5} \over \alpha }} $$ times to that of its average speed in the gas. Then, the value of $$\alpha$$ will be
(used $$\pi = {{22} \over 7}$$)
Given below are two statements: One is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: If $$d Q$$ and $$d W$$ represent the heat supplied to the system and the work done on the system respectively. Then according to the first law of thermodynamics $$d Q=d U-d W$$.
Reason R: First law of thermodynamics is based on law of conservation of energy.
In the light of the above statements, choose the correct answer from the options given below:
Match List I with List II
| List I | List II | ||
|---|---|---|---|
| A. | Isothermal Process | I. | Work done by the gas decreases internal energy |
| B. | Adiabatic Process | II. | No change in internal energy |
| C. | Isochoric Process | III. | The heat absorbed goes partly to increase internal energy and partly to do work |
| D. | Isobaric Process | IV. | No work is done on or by the gas |
Choose the correct answer from the options given below :
The graph between two temperature scales P and Q is shown in the figure. Between upper fixed point and lower fixed point there are 150 equal divisions of scale P and 100 divisions on scale Q. The relationship for conversion between the two scales is given by :-

According to law of equipartition of energy the molar specific heat of a diatomic gas at constant volume where the molecule has one additional vibrational mode is :-
The root mean square velocity of molecules of gas is
A Carnot engine with efficiency 50% takes heat from a source at 600 K. In order to increase the efficiency to 70%, keeping the temperature of sink same, the new temperature of the source will be :
Let $$\gamma_1$$ be the ratio of molar specific heat at constant pressure and molar specific heat at constant volume of a monoatomic gas and $$\gamma_2$$ be the similar ratio of diatomic gas. Considering the diatomic gas molecule as a rigid rotator, the ratio, $$\frac{\gamma_1}{\gamma_2}$$ is :
In an Isothermal change, the change in pressure and volume of a gas can be represented for three different temperature; $$\mathrm{T_3 > T_2 > T_1}$$ as :
1 g of a liquid is converted to vapour at 3 $$\times$$ 10$$^5$$ Pa pressure. If 10% of the heat supplied is used for increasing the volume by 1600 cm$$^3$$ during this phase change, then the increase in internal energy in the process will be :
Given below are two statements :
Statement I : The temperature of a gas is $$-73^\circ$$C. When the gas is heated to $$527^\circ$$C, the root mean square speed of the molecules is doubled.
Statement II : The product of pressure and volume of an ideal gas will be equal to translational kinetic energy of the molecules.
In the light of the above statements, choose the correct answer from the option given below :
A thermodynamic system is taken from an original state D to an intermediate state E by the linear process shown in the figure. Its volume is then reduced to the original volume from E to F by an isobaric process. The total work done by the gas from D to E to F will be

The root mean square speed of smoke particles of mass $$5 \times 10^{-17} \mathrm{~kg}$$ in their Brownian motion in air at NTP is approximately. [Given $$\mathrm{k}=1.38 \times 10^{-23} \mathrm{JK}^{-1}$$]
A vessel contains $$14 \mathrm{~g}$$ of nitrogen gas at a temperature of $$27^{\circ} \mathrm{C}$$. The amount of heat to be transferred to the gas to double the r.m.s speed of its molecules will be :
Take $$\mathrm{R}=8.32 \mathrm{~J} \mathrm{~mol}^{-1} \,\mathrm{k}^{-1}$$.
A Carnot engine has efficiency of $$50 \%$$. If the temperature of sink is reduced by $$40^{\circ} \mathrm{C}$$, its efficiency increases by $$30 \%$$. The temperature of the source will be:
Given below are two statements :
Statement I : The average momentum of a molecule in a sample of an ideal gas depends on temperature.
Statement II : The rms speed of oxygen molecules in a gas is $$v$$. If the temperature is doubled and the oxygen molecules dissociate into oxygen atoms, the rms speed will become $$2 v$$.
In the light of the above statements, choose the correct answer from the options given below :
In $$1^{\text {st }}$$ case, Carnot engine operates between temperatures $$300 \mathrm{~K}$$ and $$100 \mathrm{~K}$$. In $$2^{\text {nd }}$$ case, as shown in the figure, a combination of two engines is used. The efficiency of this combination (in $$2^{\text {nd }}$$ case) will be :

Which statements are correct about degrees of freedom ?
(A) A molecule with n degrees of freedom has n$$^{2}$$ different ways of storing energy.
(B) Each degree of freedom is associated with $$\frac{1}{2}$$ RT average energy per mole.
(C) A monatomic gas molecule has 1 rotational degree of freedom where as diatomic molecule has 2 rotational degrees of freedom.
(D) $$\mathrm{CH}_{4}$$ has a total of 6 degrees of freedom.
Choose the correct answer from the options given below :
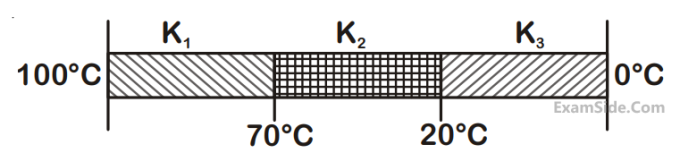
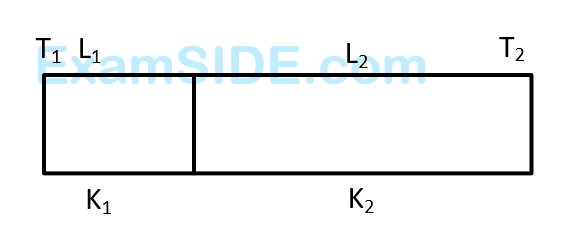
If $$K_{1}$$ and $$K_{2}$$ are the thermal conductivities, $$L_{1}$$ and $$L_{2}$$ are the lengths and $$A_{1}$$ and $$A_{2}$$ are the cross sectional areas of steel and copper rods respectively such that $$\frac{K_{2}}{K_{1}}=9, \frac{A_{1}}{A_{2}}=2, \frac{L_{1}}{L_{2}}=2$$. Then, for the arrangement as shown in the figure, the value of temperature $$\mathrm{T}$$ of the steel - copper junction in the steady state will be:

Read the following statements :
A. When small temperature difference between a liquid and its surrounding is doubled, the rate of loss of heat of the liquid becomes twice.
B. Two bodies $$P$$ and $$Q$$ having equal surface areas are maintained at temperature $$10^{\circ} \mathrm{C}$$ and $$20^{\circ} \mathrm{C}$$. The thermal radiation emitted in a given time by $$\mathrm{P}$$ and $$\mathrm{Q}$$ are in the ratio $$1: 1.15$$.
C. A Carnot Engine working between $$100 \mathrm{~K}$$ and $$400 \mathrm{~K}$$ has an efficiency of $$75 \%$$.
D. When small temperature difference between a liquid and its surrounding is quadrupled, the rate of loss of heat of the liquid becomes twice.
Choose the correct answer from the options given below :
Same gas is filled in two vessels of the same volume at the same temperature. If the ratio of the number of molecules is $$1: 4$$, then
A. The r.m.s. velocity of gas molecules in two vessels will be the same.
B. The ratio of pressure in these vessels will be $$1: 4$$.
C. The ratio of pressure will be $$1: 1$$.
D. The r.m.s. velocity of gas molecules in two vessels will be in the ratio of $$1: 4$$.
Choose the correct answer from the options given below :
An ice cube of dimensions $$60 \mathrm{~cm} \times 50 \mathrm{~cm} \times 20 \mathrm{~cm}$$ is placed in an insulation box of wall thickness $$1 \mathrm{~cm}$$. The box keeping the ice cube at $$0^{\circ} \mathrm{C}$$ of temperature is brought to a room of temperature $$40^{\circ} \mathrm{C}$$. The rate of melting of ice is approximately :
(Latent heat of fusion of ice is $$3.4 \times 10^{5} \mathrm{~J} \mathrm{~kg}^{-1}$$ and thermal conducting of insulation wall is $$0.05 \,\mathrm{Wm}^{-1 \circ} \mathrm{C}^{-1}$$ )
A gas has $$n$$ degrees of freedom. The ratio of specific heat of gas at constant volume to the specific heat of gas at constant pressure will be :
7 mol of a certain monoatomic ideal gas undergoes a temperature increase of $$40 \mathrm{~K}$$ at constant pressure. The increase in the internal energy of the gas in this process is :
(Given $$\mathrm{R}=8.3 \,\mathrm{JK}^{-1} \mathrm{~mol}^{-1}$$ )
A monoatomic gas at pressure $$\mathrm{P}$$ and volume $$\mathrm{V}$$ is suddenly compressed to one eighth of its original volume. The final pressure at constant entropy will be :
Sound travels in a mixture of two moles of helium and n moles of hydrogen. If rms speed of gas molecules in the mixture is $$\sqrt2$$ times the speed of sound, then the value of n will be :
Let $$\eta_{1}$$ is the efficiency of an engine at $$T_{1}=447^{\circ} \mathrm{C}$$ and $$\mathrm{T}_{2}=147^{\circ} \mathrm{C}$$ while $$\eta_{2}$$ is the efficiency at $$\mathrm{T}_{1}=947^{\circ} \mathrm{C}$$ and $$\mathrm{T}_{2}=47^{\circ} \mathrm{C}$$ The ratio $$\frac{\eta_{1}}{\eta_{2}}$$ will be :
A certain amount of gas of volume $$\mathrm{V}$$ at $$27^{\circ} \mathrm{C}$$ temperature and pressure $$2 \times 10^{7} \mathrm{Nm}^{-2}$$ expands isothermally until its volume gets doubled. Later it expands adiabatically until its volume gets redoubled. The final pressure of the gas will be (Use $$\gamma=1.5)$$ :
Following statements are given :
(A) The average kinetic energy of a gas molecule decreases when the temperature is reduced.
(B) The average kinetic energy of a gas molecule increases with increase in pressure at constant temperature.
(C) The average kinetic energy of a gas molecule decreases with increase in volume.
(D) Pressure of a gas increases with increase in temperature at constant pressure.
(E) The volume of gas decreases with increase in temperature.
Choose the correct answer from the options given below :
The pressure of the gas in a constant volume gas thermometer is 100 cm of mercury when placed in melting ice at 1 atm. When the bulb is placed in a liquid, the pressure becomes 180 cm of mercury. Temperature of the liquid is :
(Given 0$$^\circ$$C = 273 K)
A sample of monoatomic gas is taken at initial pressure of 75 kPa. The volume of the gas is then compressed from 1200 cm3 to 150 cm3 adiabatically. In this process, the value of workdone on the gas will be :
At what temperature a gold ring of diameter 6.230 cm be heated so that it can be fitted on a wooden bangle of diameter 6.241 cm ? Both the diameters have been measured at room temperature (27$$^\circ$$C).
(Given : coefficient of linear thermal expansion of gold $$\alpha$$L = 1.4 $$\times$$ 10$$-$$5 K$$-$$1)
Starting with the same initial conditions, an ideal gas expands from volume V1 to V2 in three different ways. The work done by the gas is W1 if the process is purely isothermal, W2, if the process is purely adiabatic and W3 if the process is purely isobaric. Then, choose the correct option
A vessel contains 16g of hydrogen and 128g of oxygen at standard temperature and pressure. The volume of the vessel in cm3 is :
A cylinder of fixed capacity of 44.8 litres contains helium gas at standard temperature and pressure. The amount of heat needed to raise the temperature of gas in the cylinder by 20.0$$^\circ$$C will be :
(Given gas constant R = 8.3 JK$$-$$1-mol$$-$$1)
In van der Waal equation $$\left[ {P + {a \over {{V^2}}}} \right]$$ [V $$-$$ b] = RT; P is pressure, V is volume, R is universal gas constant and T is temperature. The ratio of constants $${a \over b}$$ is dimensionally equal to :
A sample of an ideal gas is taken through the cyclic process ABCA as shown in figure. It absorbs, 40 J of heat during the part AB, no heat during BC and rejects 60 J of heat during CA. A work of 50 J is done on the gas during the part BC. The internal energy of the gas at A is 1560 J. The workdone by the gas during the part CA is :

What will be the effect on the root mean square velocity of oxygen molecules if the temperature is doubled and oxygen molecule dissociates into atomic oxygen?
Given below are two statements :
Statement I : When $$\mu$$ amount of an ideal gas undergoes adiabatic change from state (P1, V1, T1) to state (P2, V2, T2), then work done is $$W = {{\mu R({T_2} - {T_1})} \over {1 - \gamma }}$$, where $$\gamma = {{{C_p}} \over {{C_v}}}$$ and R = universal gas constant.
Statement II : In the above case, when work is done on the gas, the temperature of the gas would rise.
Choose the correct answer from the options given below :
For a perfect gas, two pressures P1 and P2 are shown in figure. The graph shows :

According to kinetic theory of gases,
A. The motion of the gas molecules freezes at 0$$^\circ$$C.
B. The mean free path of gas molecules decreases if the density of molecules is increased.
C. The mean free path of gas molecules increases if temperature is increased keeping pressure constant.
D. Average kinetic energy per molecule per degree of freedom is $${3 \over 2}{k_B}T$$ (for monoatomic gases).
Choose the most appropriate answer from the options given below :
A lead bullet penetrates into a solid object and melts. Assuming that 40% of its kinetic energy is used to heat it, the initial speed of bullet is :
(Given : initial temperature of the bullet = 127$$^\circ$$C, Melting point of the bullet = 327$$^\circ$$C, Latent heat of fusion of lead = 2.5 $$\times$$ 104 J kg$$-$$1, Specific heat capacity of lead = 125 J/kg K)
A mixture of hydrogen and oxygen has volume 2000 cm3, temperature 300 K, pressure 100 kPa and mass 0.76 g. The ratio of number of moles of hydrogen to number of moles of oxygen in the mixture will be:
[Take gas constant R = 8.3 JK$$-$$1mol$$-$$1]
A flask contains argon and oxygen in the ratio of 3 : 2 in mass and the mixture is kept at 27$$^\circ$$C. The ratio of their average kinetic energy per molecule respectively will be :
The efficiency of a Carnot's engine, working between steam point and ice point, will be :
A thermally insulated vessel contains an ideal gas of molecular mass M and ratio of specific heats 1.4. Vessel is moving with speed v and is suddenly brought to rest. Assuming no heat is lost to the surrounding and vessel temperature of the gas increases by :
(R = universal gas constant)
A solid metallic cube having total surface area 24 m2 is uniformly heated. If its temperature is increased by 10$$^\circ$$C, calculate the increase in volume of the cube. (Given $$\alpha$$ = 5.0 $$\times$$ 10$$-$$4 $$^\circ$$C$$-$$1).
A copper block of mass 5.0 kg is heated to a temperature of 500$$^\circ$$C and is placed on a large ice block. What is the maximum amount of ice that can melt? [Specific heat of copper : 0.39 J g$$-$$1 $$^\circ$$C$$-$$1 and latent heat of fusion of water : 335 J g$$-$$1]
The ratio of specific heats $$\left( {{{{C_P}} \over {{C_V}}}} \right)$$ in terms of degree of freedom (f) is given by :
The relation between root mean square speed (vrms) and most probable sped (vp) for the molar mass M of oxygen gas molecule at the temperature of 300 K will be :
A Carnot engine takes 5000 kcal of heat from a reservoir at 727$$^\circ$$C and gives heat to a sink at 127$$^\circ$$C. The work done by the engine is
A 100 g of iron nail is hit by a 1.5 kg hammer striking at a velocity of 60 ms$$-$$1. What will be the rise in the temperature of the nail if one fourth of energy of the hammer goes into heating the nail?
[Specific heat capacity of iron = 0.42 Jg$$-$$1 $$^\circ$$C$$-$$1]
A Carnot engine whose heat sinks at 27$$^\circ$$C, has an efficiency of 25%. By how many degrees should the temperature of the source be changed to increase the efficiency by 100% of the original efficiency?
Two metallic blocks M1 and M2 of same area of cross-section are connected to each other (as shown in figure). If the thermal conductivity of M2 is K then the thermal conductivity of M1 will be :
[Assume steady state heat conduction]

[Given 1 cal = 4.2 J and specific heat of water = 1 cal g$$-$$1 $$^\circ$$0C$$-$$1]
[Take gas constant as 8.3 J mol$$-$$1 K$$-$$1]

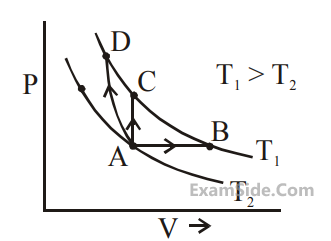
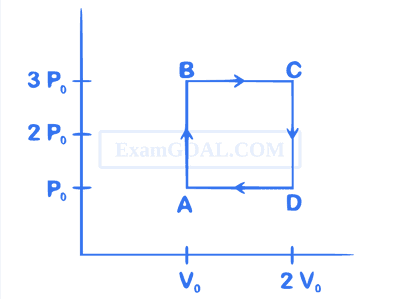
Choose the correct option out of the following for work done if processes BC and DA are adiabatic.

$$S = {\alpha ^2}\beta \ln \left[ {{{\mu kR} \over {J{\beta ^2}}} + 3} \right]$$ where $$\alpha$$ and $$\beta$$ are the constants. $$\mu$$, J, k and R are no. of moles, mechanical equivalent of heat, Boltzmann constant and gas constant respectively.
[Take $$S = {{dQ} \over T}$$]
Choose the incorrect option from the following :
(Molecular weight of oxygen is 32g/mol; R = 8.3 J K$$-$$1 mol$$-$$1)




Statement I : In a diatomic molecule, the rotational energy at a given temperature obeys Maxwell's distribution.
Statement II : In a diatomic molecule, the rotational energy at a given temperature equals the translational kinetic energy for each molecule.
In the light of the above statements, choose the correct answer from the options given below :
Assertion A : When a rod lying freely is heated, no thermal stress is developed in it.
Reason R : On heating, the length of the rod increases.
In the light of the above statements, choose the correct answer from the options given below :

| List I | List II | ||
|---|---|---|---|
| (a) | Isothermal | (i) | Pressure constant |
| (b) | Isochoric | (ii) | Temperature constant |
| (c) | Adiabatic | (iii) | Volume constant |
| (d) | Isobaric | (iv) | Heat content is constant |
Choose the correct answer from the options given below :
A $$ \to $$ B : Isothermal expansion at temperature T so that the volume is doubled from V1 to V2 = 2V1 and pressure charges from P1 to P2
B $$ \to $$ C : Isobaric compression at pressure P2 to initial volume V1.
C $$ \to $$ A : Isochoric change leading to change of pressure from P2 to P1.
Total workdone in the complete cycle ABCA is :

$$\gamma \left( { = {{{C_p}} \over {{C_v}}}} \right)$$ are given, respectively by:
The correct relation between these parameters are :
(Given, mean kinetic energy of a molecule
(at T) is 4 $$ \times $$ 10–14 erg, g = 980 cm/s2, density of
mercury = 13.6 g/cm3)
| Process | Condition |
|---|---|
| (I) Adiabatic | (1) $$\Delta $$W = 0 |
| (II) Isothermal | (2) $$\Delta $$Q = 0 |
| (III) Isochoric | (3) $$\Delta $$U $$ \ne $$ 0, $$\Delta $$W $$ \ne $$ 0, $$\Delta $$Q $$ \ne $$ 0 |
| (IV) Isobaric | (4) $$\Delta $$U = 0 |
| Molecule Type | CP/CV |
|---|---|
| (A) Monatomic | (I) 7/5 |
| (B) Diatomic rigid molecules | (II) 9/7 |
| (C) Diatomic non-rigid molecules | (III) 4/3 |
| (D) Triatomic rigid molecules | (IV) 5/3 |
= 4200 J kg-1K-1 and the latent heat of
ice = 3.4 $$ \times $$ 105 J kg–1. 100 grams of ice at
0oC is placed in 200 g of water at 25oC. The
amount of ice that will melt as the temperature
of water reaches 0oC is close to (in grams) :
(Latent heat of water = 540 cal g–1, specific heat of water = 1 cal g–1 oC–1)
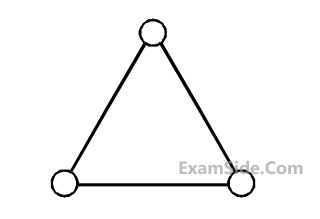 Consider a gas of triatomic molecules. The
molecules are assumed to be triangular and
made of massless rigid rods whose vertices
are occupied by atoms. The internal energy of
a mole of the gas at temperature T is :
Consider a gas of triatomic molecules. The
molecules are assumed to be triangular and
made of massless rigid rods whose vertices
are occupied by atoms. The internal energy of
a mole of the gas at temperature T is :(A) the mean free path of the molecules decreases.
(B) the mean collision time between the molecules decreases.
(C) the mean free path remains unchanged.
(D) the mean collision time remains unchanged.
(Graphs are schematic and are not to scale)

(Graphs are schematic and not drawn to scale)
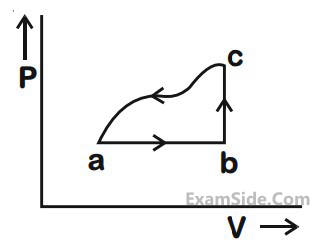
 The P-V diagram that best describes this cycle
is :
The P-V diagram that best describes this cycle
is :(Diagrams are schematic and not to scale)
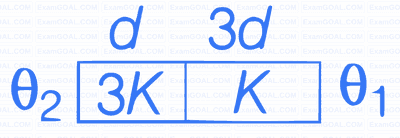
[Boltzmann Constant kB = 1.38 × 10–23 J/K Avogadro Number NA = 6.02 × 1026 /kg Radius of Earth : 6.4 × 106 m Gravitational acceleration on Earth = 10ms–2]
(R is universal gas constant and g is the acceleration due to gravity)
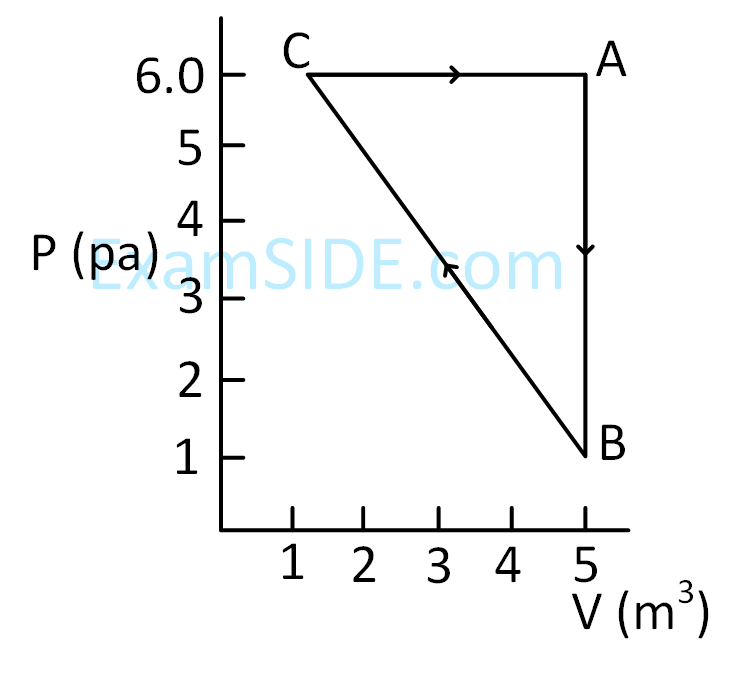

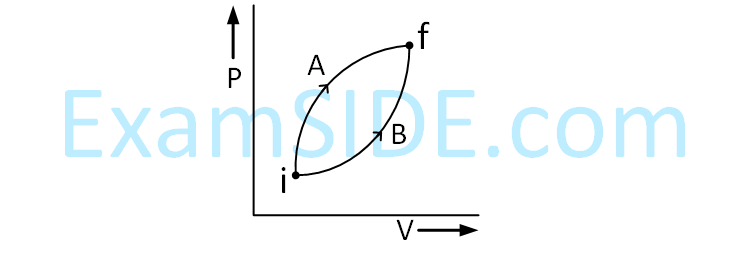
When path ACB is used 60 J of heat flows into the system and 30 J of work is done by the system. If path ADB is used work done by the system is 10 J. The heat Flow into the system in path ADB is :

[kB =1.4 $$ \times $$ 10-23 J/K; mHe = 7 $$ \times $$ 10 -27 kg ]
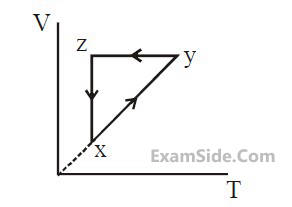
out of the following which one correctly represents the T-P diagram ?

CP – Cv = a for hydrogen gas
CP – Cv = b for nitrogen gas
The correct relation between a and b is
$$(i)$$ Sequentially keeping in contact with $$2$$ reservoirs such that each reservoir
$$\,\,\,\,\,\,\,\,$$supplies same amount of heat.
$$(ii)$$ Sequentially keeping in contact with $$8$$ reservoirs such that each reservoir
$$\,\,\,\,\,\,\,\,\,\,$$supplies same amount of heat.
In both the cases body is brought from initial temperature $${100^ \circ }C$$ to final temperature $${200^ \circ }C$$. Entropy change of the body in the two cases respectively is :

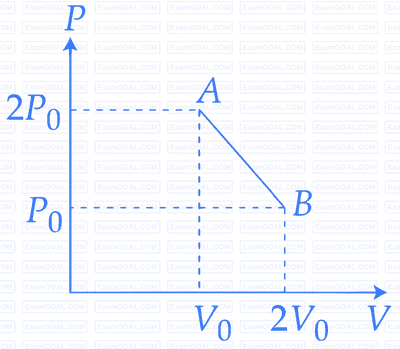
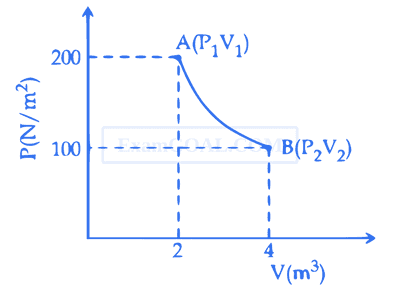
The above $$p$$-$$v$$ diagram represents the thermodynamic cycle of an engine, operating with an ideal monatomic gas. The amount of heat, extracted from the source in a single cycle is
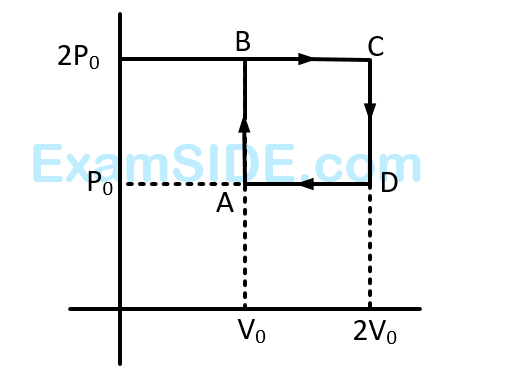


The net work done on the gas in the cycle $$ABCDA$$ is:

Assuming the gas to be ideal the work done on the gas in taking it from $$A$$ to $$B$$ is :
Statement - 2: $$R = {R_0}\left( {1 + \alpha \,\Delta t} \right)$$ is valid only when the change in the temperature $$\Delta T$$ is small and $$\Delta T = \left( {R - {R_0}} \right) < < {R_0}.$$

The work done on the gas in taking it from $$D$$ to $$A$$ is :
Where r0 is the radius of the Earth and $$\sigma $$ is Stefan's constant.

Numerical
A wire of length 10 cm and diameter 0.5 mm is used in a bulb. The temperature of the wire is $1727^{\circ} \mathrm{C}$ and power radiated by the wire is 94.2 W . Its emissivity is $\frac{x}{8}$ where $x=$ _________.
(Given $\sigma=6.0 \times 10^{-8} \mathrm{~W} \mathrm{~m}^{-2} \mathrm{~K}^{-4}, \pi=3.14$ and assume that the emissivity of wire material is same at all wavelength.)
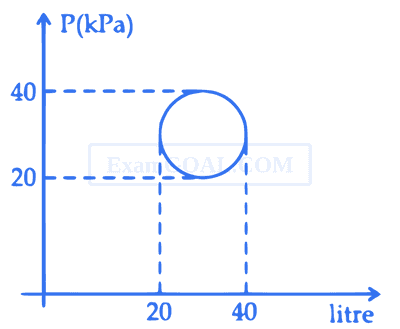
An ideal gas has undergone through the cyclic process as shown in the figure. Work done by the gas in the entire cycle is ________ $\times 10^{-1} \mathrm{~J}$. (Take $\pi=3.14$ )

The internal energy of air in $4 \mathrm{~m} \times 4 \mathrm{~m} \times 3 \mathrm{~m}$ sized room at 1 atmospheric pressure will be___________________$\times 10^6 \mathrm{~J}$
(Consider air as diatomic molecule)
$\gamma_{\mathrm{A}}$ is the specific heat ratio of monoatomic gas A having 3 translational degrees of freedom. $\gamma_B$ is the specific heat ratio of polyatomic gas $B$ having 3 translational, 3 rotational degrees of freedom and 1 vibrational mode. If $\frac{\gamma_A}{\gamma_B}=\left(1+\frac{1}{n}\right)$, then the value of $n$ is ________ .
A container of fixed volume contains a gas at 27°C. To double the pressure of the gas, the temperature of gas should be raised to _____ °C.
The temperature of 1 mole of an ideal monoatomic gas is increased by $50^{\circ} \mathrm{C}$ at constant pressure. The total heat added and change in internal energy are $E_1$ and $E_2$, respectively. If $\frac{E_1}{E_2}=\frac{x}{9}$ then the value of $x$ is _________.
An ideal gas initially at $0^{\circ} \mathrm{C}$ temperature, is compressed suddenly to one fourth of its volume. If the ratio of specific heat at constant pressure to that at constant volume is $3 / 2$, the change in temperature due to the thermodynamic process is _________ K.
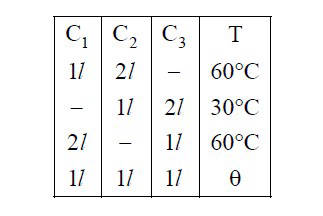
Three conductors of same length having thermal conductivity $k_1, k_2$ and $k_3$ are connected as shown in figure.

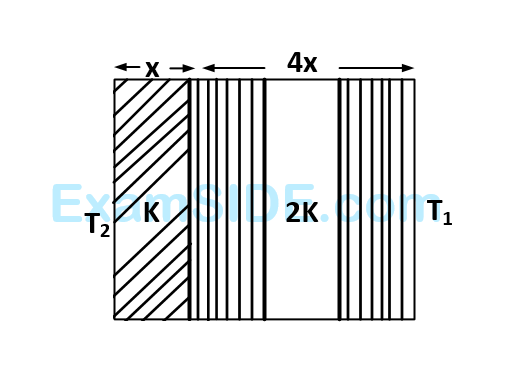
Area of cross sections of $1^{\text {st }}$ and $2^{\text {nd }}$ conductor are same and for $3^{\text {rd }}$ conductor it is double of the $1^{\text {st }}$ conductor. The temperatures are given in the figure. In steady state condition, the value of $\theta$ is _________ ${ }^{\circ} \mathrm{C}$. (Given : $\mathrm{k}_1=60 \mathrm{Js}^{-1} \mathrm{~m}^{-1} \mathrm{~K}^{-1}, \mathrm{k}_2=120 \mathrm{Js}^{-1} \mathrm{~m}^{-1} \mathrm{~K}^{-1}, \mathrm{k}_3=135 \mathrm{Js}^{-1} \mathrm{~m}^{-1} \mathrm{~K}^{-1}$ )
Two plates $$\mathrm{A}$$ and $$\mathrm{B}$$ have thermal conductivities $$84 ~\mathrm{Wm}^{-1} \mathrm{~K}^{-1}$$ and $$126 ~\mathrm{Wm}^{-1} \mathrm{~K}^{-1}$$ respectively. They have same surface area and same thickness. They are placed in contact along their surfaces. If the temperatures of the outer surfaces of $$\mathrm{A}$$ and $$\mathrm{B}$$ are kept at $$100^{\circ} \mathrm{C}$$ and $$0{ }^{\circ} \mathrm{C}$$ respectively, then the temperature of the surface of contact in steady state is _____________ $${ }^{\circ} \mathrm{C}$$.
A steel rod of length $$1 \mathrm{~m}$$ and cross sectional area $$10^{-4} \mathrm{~m}^{2}$$ is heated from $$0^{\circ} \mathrm{C}$$ to $$200^{\circ} \mathrm{C}$$ without being allowed to extend or bend. The compressive tension produced in the rod is ___________ $$\times 10^{4} \mathrm{~N}$$. (Given Young's modulus of steel $$=2 \times 10^{11} \mathrm{Nm}^{-2}$$, coefficient of linear expansion $$=10^{-5} \mathrm{~K}^{-1}$$ )
(Assume that the specific heat capacity of water remains constant over the temperature range of the water).
A hole is drilled in a metal sheet. At $$\mathrm{27^\circ C}$$, the diameter of hole is 5 cm. When the sheet is heated to $$\mathrm{177^\circ C}$$, the change in the diameter of hole is $$\mathrm{d\times10^{-3}}$$ cm. The value of d will be __________ if coefficient of linear expansion of the metal is $$1.6\times10^{-5}/^\circ$$C.
The pressure $$\mathrm{P}_{1}$$ and density $$\mathrm{d}_{1}$$ of diatomic gas $$\left(\gamma=\frac{7}{5}\right)$$ changes suddenly to $$\mathrm{P}_{2}\left(>\mathrm{P}_{1}\right)$$ and $$\mathrm{d}_{2}$$ respectively during an adiabatic process. The temperature of the gas increases and becomes ________ times of its initial temperature. (given $$\frac{\mathrm{d}_{2}}{\mathrm{~d}_{1}}=32$$)
One mole of a monoatomic gas is mixed with three moles of a diatomic gas. The molecular specific heat of mixture at constant volume is $$\frac{\alpha^{2}}{4} \mathrm{R} \,\mathrm{J} / \mathrm{mol} \,\mathrm{K}$$; then the value of $$\alpha$$ will be _________. (Assume that the given diatomic gas has no vibrational mode).
At a certain temperature, the degrees of freedom per molecule for gas is 8. The gas performs 150 J of work when it expands under constant pressure. The amount of heat absorbed by the gas will be _________ J.
A block of ice of mass 120 g at temperature 0$$^\circ$$C is put in 300 g of water at 25$$^\circ$$C. The x g of ice melts as the temperature of the water reaches 0$$^\circ$$C. The value of x is _____________.
[Use specific heat capacity of water = 4200 Jkg$$-$$1K$$-$$1, Latent heat of ice = 3.5 $$\times$$ 105 Jkg$$-$$1]
A unit scale is to be prepared whose length does not change with temperature and remains $$20 \mathrm{~cm}$$, using a bimetallic strip made of brass and iron each of different length. The length of both components would change in such a way that difference between their lengths remains constant. If length of brass is $$40 \mathrm{~cm}$$ and length of iron will be __________ $$\mathrm{cm}$$. $$\left(\alpha_{\text {iron }}=1.2 \times 10^{-5} \mathrm{~K}^{-1}\right.$$ and $$\left.\alpha_{\text {brass }}=1.8 \times 10^{-5} \mathrm{~K}^{-1}\right)$$.
Two coils require 20 minutes and 60 minutes respectively to produce same amount of heat energy when connected separately to the same source. If they are connected in parallel arrangement to the same source; the time required to produce same amount of heat by the combination of coils, will be ___________ min.
As per the given figure, two plates A and B of thermal conductivity K and 2 K are joined together to form a compound plate. The thickness of plates are 4.0 cm and 2.5 cm respectively and the area of cross-section is 120 cm2 for each plate. The equivalent thermal conductivity of the compound plate is $$\left( {1 + {5 \over \alpha }} \right)$$ K, then the value of $$\alpha$$ will be ______________.

300 cal. of heat is given to a heat engine and it rejects 225 cal. If source temperature is 227$$^\circ$$C, then the temperature of sink will be ______________ $$^\circ$$C.
The total internal energy of two mole monoatomic ideal gas at temperature T = 300 K will be _____________ J. (Given R = 8.31 J/mol.K)
A diatomic gas ($$\gamma$$ = 1.4) does 400J of work when it is expanded isobarically. The heat given to the gas in the process is __________ J.
In a carnot engine, the temperature of reservoir is 527$$^\circ$$C and that of sink is 200 K. If the work done by the engine when it transfers heat from reservoir to sink is 12000 kJ, the quantity of heat absorbed by the engine from reservoir is ______________ $$\times$$ 106 J.
A geyser heats water flowing at a rate of 2.0 kg per minute from 30$$^\circ$$C to 70$$^\circ$$C. If geyser operates on a gas burner, the rate of combustion of fuel will be ___________ g min$$-$$1.
[Heat of combustion = 8 $$\times$$ 103 Jg$$-$$1, Specific heat of water = 4.2 Jg$$-$$1 $$^\circ$$C$$-$$1]
A heat engine operates with the cold reservoir at temperature 324 K. The minimum temperature of the hot reservoir, if the heat engine takes 300 J heat from the hot reservoir and delivers 180 J heat to the cold reservoir per cycle, is ____________ K.
When a gas filled in a closed vessel is heated by raising the temperature by 1$$^\circ$$C, its pressure increases by 0.4%. The initial temperature of the gas is ___________ K.
A steam engine intakes 50 g of steam at 100$$^\circ$$C per minute and cools it down to 20$$^\circ$$C. If latent heat of vaporization of steam is 540 cal g$$-$$1, then the heat rejected by the steam engine per minute is __________ $$\times$$ 103 cal.
(Given : specific heat capacity of water : 1 cal g$$-$$1 $$^\circ$$C$$-$$1)
A monoatomic gas performs a work of $${Q \over {4}}$$ where Q is the heat supplied to it. The molar heat capacity of the gas will be ______________ R during this transformation. Where R is the gas constant.
0.056 kg of Nitrogen is enclosed in a vessel at a temperature of 127$$^\circ$$C. Th amount of heat required to double the speed of its molecules is ____________ k cal.
Take R = 2 cal mole$$-$$1 K$$-$$1)

(Young's modulus of material of track is 1011 Nm$$-$$2)
(Molar mass of N2 gas 28 g).
If |$$\Delta $$T| = C|$$\Delta $$P| then value of C in (K/atm.) is _________.
ideal diatomic gas ($$\gamma $$ = 1.4) is first compressed
adiabatically from volume V1 to V2 = $${{{V_1}} \over {16}}$$. It is
then allowed to expand isobarically to volume 2V2. If all the processes are the quasi-static then
the final temperature of the gas (in oK) is (to the nearest integer) _____.
 The value of $$\theta $$ (in °C to the nearest integer) is ..........
The value of $$\theta $$ (in °C to the nearest integer) is ..........5 $$ \times $$ 10-5/oC along the x-axis and 5 $$ \times $$ 10-6/oC along the y and the z-axis. If the coefficient of volume expansion of the solid is C $$ \times $$ 10-6/oC then the value of C is
