Circular Motion · Physics · JEE Main
MCQ (Single Correct Answer)
A wheel is rolling on a plane surface. The speed of a particle on the highest point of the rim is $8 \mathrm{~m} / \mathrm{s}$. The speed of the particle on the rim of the wheel at the same level as the centre of wheel, will be :

A body of mass ‘m’ connected to a massless and unstretchable string goes in vertical circle of radius ‘R’ under gravity g. The other end of the string is fixed at the center of circle. If velocity at top of circular path is $n\sqrt{ g R}$ , where, n ≥ 1, then ratio of kinetic energy of the body at bottom to that at top of the circle is :
A car of mass ' $m$ ' moves on a banked road having radius ' $r$ ' and banking angle $\theta$. To avoid slipping from banked road, the maximum permissible speed of the car is $v_0$. The coefficient of friction $\mu$ between the wheels of the car and the banked road is
A body of mass 100 g is moving in circular path of radius 2 m on vertical plane as shown in figure. The velocity of the body at point $A$ is $10 \mathrm{~m} / \mathrm{s}$. The ratio of its kinetic energies at point B and C is :

(Take acceleration due to gravity as $10 \mathrm{~m} / \mathrm{s}^2$)
A bob of mass $m$ is suspended at a point $O$ by a light string of length $l$ and left to perform vertical motion (circular) as shown in figure. Initially, by applying horizontal velocity $v_0$ at the point ' A ', the string becomes slack when, the bob reaches at the point ' $D$ '. The ratio of the kinetic energy of the bob at the points B and C is _________.

A clock has $$75 \mathrm{~cm}, 60 \mathrm{~cm}$$ long second hand and minute hand respectively. In 30 minutes duration the tip of second hand will travel $$x$$ distance more than the tip of minute hand. The value of $$x$$ in meter is nearly (Take $$\pi=3.14$$) :
A car of $$800 \mathrm{~kg}$$ is taking turn on a banked road of radius $$300 \mathrm{~m}$$ and angle of banking $$30^{\circ}$$. If coefficient of static friction is 0.2 then the maximum speed with which car can negotiate the turn safely: $$(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2, \sqrt{3}=1.73)$$
A man carrying a monkey on his shoulder does cycling smoothly on a circular track of radius $$9 \mathrm{~m}$$ and completes 120 resolutions in 3 minutes. The magnitude of centripetal acceleration of monkey is (in $$\mathrm{m} / \mathrm{s}^2$$ ) :
A cyclist starts from the point $$P$$ of a circular ground of radius $$2 \mathrm{~km}$$ and travels along its circumference to the point $$\mathrm{S}$$. The displacement of a cyclist is:

If this particle is projected with the same speed at an angle $\theta$ to the horizontal, the maximum height attained by it is equal to $4 R$. The angle of projection $\theta$ is then given by :
A coin is placed on a disc. The coefficient of friction between the coin and the disc is $$\mu$$. If the distance of the coin from the center of the disc is $$r$$, the maximum angular velocity which can be given to the disc, so that the coin does not slip away, is :
A stone of mass $$900 \mathrm{~g}$$ is tied to a string and moved in a vertical circle of radius $$1 \mathrm{~m}$$ making $$10 \mathrm{~rpm}$$. The tension in the string, when the stone is at the lowest point is (if $$\pi^2=9.8$$ and $$g=9.8 \mathrm{~m} / \mathrm{s}^2$$) :
If the radius of curvature of the path of two particles of same mass are in the ratio $$3: 4$$, then in order to have constant centripetal force, their velocities will be in the ratio of :
A train is moving with a speed of $$12 \mathrm{~m} / \mathrm{s}$$ on rails which are $$1.5 \mathrm{~m}$$ apart. To negotiate a curve radius $$400 \mathrm{~m}$$, the height by which the outer rail should be raised with respect to the inner rail is (Given, $$g=10 \mathrm{~m} / \mathrm{s}^2)$$ :
A vehicle of mass $$200 \mathrm{~kg}$$ is moving along a levelled curved road of radius $$70 \mathrm{~m}$$ with angular velocity of $$0.2 ~\mathrm{rad} / \mathrm{s}$$. The centripetal force acting on the vehicle is:
A coin placed on a rotating table just slips when it is placed at a distance of $$1 \mathrm{~cm}$$ from the center. If the angular velocity of the table in halved, it will just slip when placed at a distance of _________ from the centre :
As shown in the figure, a particle is moving with constant speed $$\pi ~\mathrm{m} / \mathrm{s}$$. Considering its motion from $$\mathrm{A}$$ to $$\mathrm{B}$$, the magnitude of the average velocity is :

A child of mass $$5 \mathrm{~kg}$$ is going round a merry-go-round that makes 1 rotation in $$3.14 \mathrm{~s}$$. The radius of the merry-go-round is $$2 \mathrm{~m}$$. The centrifugal force on the child will be
A particle is moving with constant speed in a circular path. When the particle turns by an angle $$90^{\circ}$$, the ratio of instantaneous velocity to its average velocity is $$\pi: x \sqrt{2}$$. The value of $$x$$ will be -
A small block of mass $$100 \mathrm{~g}$$ is tied to a spring of spring constant $$7.5 \mathrm{~N} / \mathrm{m}$$ and length $$20 \mathrm{~cm}$$. The other end of spring is fixed at a particular point A. If the block moves in a circular path on a smooth horizontal surface with constant angular velocity $$5 ~\mathrm{rad} / \mathrm{s}$$ about point $$\mathrm{A}$$, then tension in the spring is -
An object moves at a constant speed along a circular path in a horizontal plane with center at the origin. When the object is at $$x=+2~\mathrm{m}$$, its velocity is $$\mathrm{ - 4\widehat j}$$ m/s. The object's velocity (v) and acceleration (a) at $$x=-2~\mathrm{m}$$ will be
A car is moving on a horizontal curved road with radius 50 m. The approximate maximum speed of car will be, if friction between tyres and road is 0.34. [take g = 10 ms$$^{-2}$$]
A car is moving with a constant speed of 20 m/s in a circular horizontal track of radius 40 m. A bob is suspended from the roof of the car by a massless string. The angle made by the string with the vertical will be : (Take g = 10 m/s$$^2$$)
A body of mass 200g is tied to a spring of spring constant 12.5 N/m, while the other end of spring is fixed at point O. If the body moves about O in a circular path on a smooth horizontal surface with constant angular speed 5 rad/s. Then the ratio of extension in the spring to its natural length will be :
A smooth circular groove has a smooth vertical wall as shown in figure. A block of mass m moves against the wall with a speed v. Which of the following curve represents the correct relation between the normal reaction on the block by the wall (N) and speed of the block (v) ?

A person moved from A to B on a circular path as shown in figure. If the distance travelled by him is $$60 \mathrm{~m}$$, then the magnitude of displacement would be :
(Given $$\left.\cos 135^{\circ}=-0.7\right)$$

A particle of mass m is moving in a circular path of constant radius r such that its centripetal acceleration (a) is varying with time t as a = k2rt2, where k is a constant. The power delivered to the particle by the force acting on it is given as
A stone tide to a spring of length L is whirled in a vertical circle with the other end of the spring at the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of change in its velocity, as it reaches a position where the string is horizontal, is $$\sqrt {x({u^2} - gL)} $$. The value of x is -
A ball is released from rest from point P of a smooth semi-spherical vessel as shown in figure. The ratio of the centripetal force and normal reaction on the ball at point Q is A while angular position of point Q is $$\alpha$$ with respect to point P. Which of the following graphs represent the correct relation between A and $$\alpha$$ when ball goes from Q to R?

A disc with a flat small bottom beaker placed on it at a distance R from its center is revolving about an axis passing through the center and perpendicular to its plane with an angular velocity $$\omega$$. The coefficient of static friction between the bottom of the beaker and the surface of the disc is $$\mu$$. The beaker will revolve with the disc if :
For a particle in uniform circular motion, the acceleration $$\overrightarrow a $$ at any point P(R, $$\theta$$) on the circular path of radius R is (when $$\theta$$ is measured from the positive x-axis and v is uniform speed) :
A stone of mass m, tied to a string is being whirled in a vertical circle with a uniform speed. The tension in the string is
A fly wheel is accelerated uniformly from rest and rotates through 5 rad in the first second. The angle rotated by the fly wheel in the next second, will be :
A boy ties a stone of mass 100 g to the end of a 2 m long string and whirls it around in a horizontal plane. The string can withstand the maximum tension of 80 N. If the maximum speed with which the stone can revolve is $${K \over \pi }$$ rev./min. The value of K is :
(Assume the string is massless and unstretchable)
Given : 1 ly = 9.46 $$\times$$ 1015 m
1 AU = 1.5 $$\times$$ 1011 m
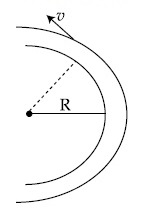
Statement II : If the road is banked at an angle of 45$$^\circ$$, cyclist can cross the curve of 2m radius with the speed of 18.5 kmh$$-$$1 without slipping.
In the light of the above statements, choose the correct answer from the options given below.
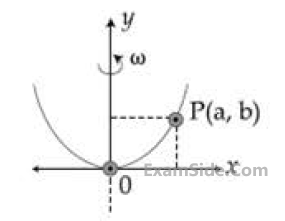
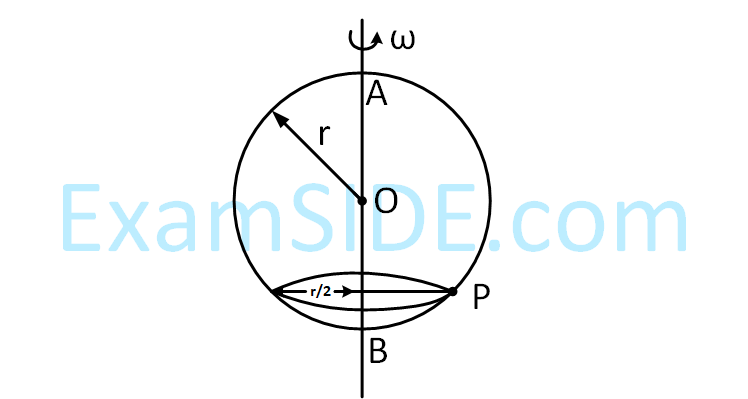
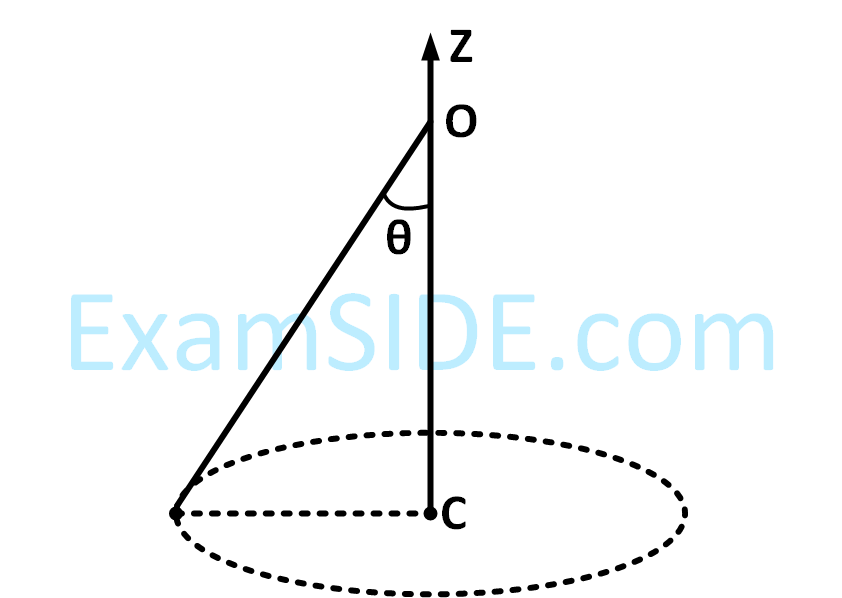

Numerical
A particle of charge $1.6 \mu \mathrm{C}$ and mass $16 \mu \mathrm{~g}$ is present in a strong magnetic field of 6.28 T . The particle is then fired perpendicular to magnetic field. The time required for the particle to return to original location for the first time is _________ s. $(\pi=3.14)$

A string of length $L$ is fixed at one end and carries a mass of $M$ at the other end. The mass makes $\left(\frac{3}{\pi}\right)$ rotations per second about the vertical axis passing through end of the string as shown. The tension in the string is __________ ML.
A tube of length 1 m is filled completely with an ideal liquid of mass 2 M , and closed at both ends. The tube is rotated uniformly in horizontal plane about one of its ends. If the force exerted by the liquid at the other end is F then angular velocity of the tube is $\sqrt{\frac{\mathrm{F}}{\alpha \mathrm{M}}}$ in SI unit. The value of $\alpha$ is _________.
A particle is moving in a circle of radius $$50 \mathrm{~cm}$$ in such a way that at any instant the normal and tangential components of it's acceleration are equal. If its speed at $$\mathrm{t}=0$$ is $$4 \mathrm{~m} / \mathrm{s}$$, the time taken to complete the first revolution will be $$\frac{1}{\alpha}\left[1-e^{-2 \pi}\right] \mathrm{s}$$, where $$\alpha=$$ _________.
A car is moving on a circular path of radius 600 m such that the magnitudes of the tangential acceleration and centripetal acceleration are equal. The time taken by the car to complete first quarter of revolution, if it is moving with an initial speed of 54 km/hr is $$t(1-e^{-\pi/2})s$$. The value of t is ____________.
A person starts his journey from centre 'O' of the park and comes back to the same position following path OPQO as shown in the figure. The radius of path taken by the person is 200 m and he takes 3 min 58 sec to complete his journey. The average speed of the person is _____________ ms$$-$$1. (take $$\pi$$ = 3.14)

A pendulum of length 2 m consists of a wooden bob of mass 50 g. A bullet of mass 75 g is fired towards the stationary bob with a speed v. The bullet emerges out of the bob with a speed $${v \over 3}$$ and the bob just completes the vertical circle. The value of v is ___________ ms$$-$$1. (if g = 10 m/s2).
A curved in a level road has a radius 75 m. The maximum speed of a car turning this curved road can be 30 m/s without skidding. If radius of curved road is changed to 48 m and the coefficient of friction between the tyres and the road remains same, then maximum allowed speed would be ___________ m/s.