Waves · Physics · JEE Main
MCQ (Single Correct Answer)
Given below are two statements: one is labelled as $\mathbf{A s s e r t i o n} \mathbf{A}$ and the other is labelled as Reason $\mathbf{R}$
Assertion A: A sound wave has higher speed in solids than gases.
Reason R: Gases have higher value of Bulk modulus than solids.
In the light of the above statements, choose the correct answer from the options given below
The equation of a transverse wave travelling along a string is $y(x, t)=4.0 \sin \left[20 \times 10^{-3} x+600 t\right] \mathrm{mm}$, where $x$ is in mm and $t$ is in second. The velocity of the wave is :
A closed organ and an open organ tube are filled by two different gases having same bulk modulus but different densities $\rho_1$ and $\rho_2$, respectively. The frequency of $9^{\text {th }}$ harmonic of closed tube is identical with $4^{\text {th }}$ harmonic of open tube. If the length of the closed tube is 10 cm and the density ratio of the gases is $\rho_1: \rho_2=1: 16$, then the length of the open tube is :
A plane progressive wave is given by $$y=2 \cos 2 \pi(330 \mathrm{t}-x) \mathrm{m}$$. The frequency of the wave is :
The fundamental frequency of a closed organ pipe is equal to the first overtone frequency of an open organ pipe. If length of the open pipe is $$60 \mathrm{~cm}$$, the length of the closed pipe will be:
A car P travelling at $$20 \mathrm{~ms}^{-1}$$ sounds its horn at a frequency of $$400 \mathrm{~Hz}$$. Another car $$\mathrm{Q}$$ is travelling behind the first car in the same direction with a velocity $$40 \mathrm{~ms}^{-1}$$. The frequency heard by the passenger of the car $$\mathrm{Q}$$ is approximately [Take, velocity of sound $$=360 \mathrm{~ms}^{-1}$$ ]
For a periodic motion represented by the equation
$$y=\sin \omega \mathrm{t}+\cos \omega \mathrm{t}$$
the amplitude of the motion is
The engine of a train moving with speed $$10 \mathrm{~ms}^{-1}$$ towards a platform sounds a whistle at frequency $$400 \mathrm{~Hz}$$. The frequency heard by a passenger inside the train is: (neglect air speed. Speed of sound in air $$=330 \mathrm{~ms}^{-1}$$ )
A steel wire with mass per unit length $$7.0 \times 10^{-3} \mathrm{~kg} \mathrm{~m}^{-1}$$ is under tension of $$70 \mathrm{~N}$$. The speed of transverse waves in the wire will be:
A person observes two moving trains, 'A' reaching the station and 'B' leaving the station with equal speed of $$30 \mathrm{~m} / \mathrm{s}$$. If both trains emit sounds with frequency $$300 \mathrm{~Hz}$$, (Speed of sound: $$330 \mathrm{~m} / \mathrm{s}$$) approximate difference of frequencies heard by the person will be:
A travelling wave is described by the equation
$$y(x,t) = [0.05\sin (8x - 4t)]$$ m
The velocity of the wave is : [all the quantities are in SI unit]
In the wave equation
$$ y=0.5 \sin \frac{2 \pi}{\lambda}(400 \mathrm{t}-x) \,\mathrm{m} $$
the velocity of the wave will be:
A transverse wave is represented by $$y=2 \sin (\omega t-k x)\, \mathrm{cm}$$. The value of wavelength (in $$\mathrm{cm}$$) for which the wave velocity becomes equal to the maximum particle velocity, will be :
Which of the following equations correctly represents a travelling wave having wavelength $$\lambda$$ = 4.0 cm, frequency v = 100 Hz and travelling in positive x-axis direction?
A longitudinal wave is represented by $$x = 10\sin 2\pi \left( {nt - {x \over \lambda }} \right)$$ cm. The maximum particle velocity will be four times the wave velocity if the determined value of wavelength is equal to :
The velocity of sound in a gas, in which two wavelengths 4.08 m and 4.16 m produce 40 beats in 12s, will be :
If a wave gets refracted into a denser medium, then which of the following is true?
An observer moves towards a stationary source of sound with a velocity equal to one-fifth of the velocity of sound. The percentage change in the frequency will be :
The equations of two waves are given by :
y1 = 5 sin 2$$\pi$$(x - vt) cm
y2 = 3 sin 2$$\pi$$(x $$-$$ vt + 1.5) cm
These waves are simultaneously passing through a string. The amplitude of the resulting wave is :
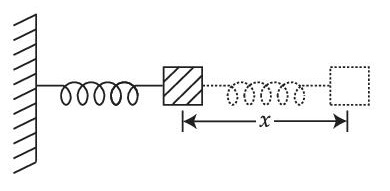
The equation of motion is given by
x(t) = A sin$$\omega$$t + B cos$$\omega$$t with $$\omega$$ = $$\sqrt {{K \over m}} $$
Suppose that at time t = 0, the position of mass is x(0) and velocity v(0), then its displacement can also be represented as x(t) = C cos($$\omega$$t $$-$$ $$\phi$$), where C and $$\phi$$ are :
(t0 represents the instant when the distance between the source and observer is minimum)
For this wave, the phase $$\phi $$ is :
(speed of sound in air = 340 ms–1) :-
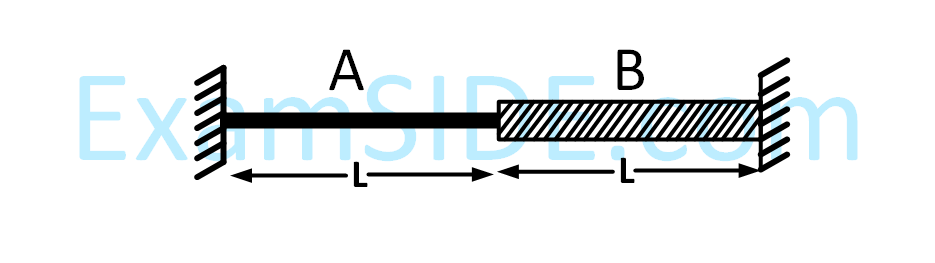A wire of length 2L, is made by joining two
wires A and B of same length but different radii
r and 2r and made of the same material. It is
vibrating at a frequency such that the joint of
the two wires forms a node. If the number of
antinodes in wire A is p and that in B is q then
the ratio p : q is :y(x, t) = 0.5 sin $$\left( {{{5\pi } \over 4}x} \right)\,$$ cos(200 $$\pi $$t).
What is the speed of the travelling wave moving in the positive x direction ?
(x and t are in meter and second, respectively.)
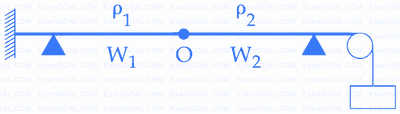
(take $${\,\,g = 10m{s^{ - 2}}}$$ )
The tension in the string is
where $$x$$ is expressed in metres and $$t$$ in seconds. The speed of the wave - motion, in $$m{s^{ - 1}}$$, is
Numerical
A closed and an open organ pipe have same lengths. If the ratio of frequencies of their seventh overtones is $$\left(\frac{a-1}{a}\right)$$ then the value of $$a$$ is _________.
Two open organ pipes of lengths $$60 \mathrm{~cm}$$ and $$90 \mathrm{~cm}$$ resonate at $$6^{\text {th }}$$ and $$5^{\text {th }}$$ harmonics respectively. The difference of frequencies for the given modes is _________ $$\mathrm{Hz}$$. (Velocity of sound in air $$=333 \mathrm{~m} / \mathrm{s}$$)
A sonometer wire of resonating length $$90 \mathrm{~cm}$$ has a fundamental frequency of $$400 \mathrm{~Hz}$$ when kept under some tension. The resonating length of the wire with fundamental frequency of $$600 \mathrm{~Hz}$$ under same tension _______ $$\mathrm{cm}$$.
A point source is emitting sound waves of intensity $$16 \times 10^{-8} \mathrm{~Wm}^{-2}$$ at the origin. The difference in intensity (magnitude only) at two points located at a distances of $$2 m$$ and $$4 m$$ from the origin respectively will be _________ $$\times 10^{-8} \mathrm{~Wm}^{-2}$$.
In a closed organ pipe, the frequency of fundamental note is $$30 \mathrm{~Hz}$$. A certain amount of water is now poured in the organ pipe so that the fundamental frequency is increased to $$110 \mathrm{~Hz}$$. If the organ pipe has a cross-sectional area of $$2 \mathrm{~cm}^2$$, the amount of water poured in the organ tube is __________ g. (Take speed of sound in air is $$330 \mathrm{~m} / \mathrm{s}$$)
A closed organ pipe $$150 \mathrm{~cm}$$ long gives 7 beats per second with an open organ pipe of length $$350 \mathrm{~cm}$$, both vibrating in fundamental mode. The velocity of sound is __________ $$\mathrm{m} / \mathrm{s}$$.
In an experiment with sonometer when a mass of $$180 \mathrm{~g}$$ is attached to the string, it vibrates with fundamental frequency of $$30 \mathrm{~Hz}$$. When a mass $$\mathrm{m}$$ is attached, the string vibrates with fundamental frequency of $$50 \mathrm{~Hz}$$. The value of $$\mathrm{m}$$ is ___________ g.
For a certain organ pipe, the first three resonance frequencies are in the ratio of $$1:3:5$$ respectively. If the frequency of fifth harmonic is $$405 \mathrm{~Hz}$$ and the speed of sound in air is $$324 \mathrm{~ms}^{-1}$$ the length of the organ pipe is _________ $$\mathrm{m}$$.
The equation of wave is given by
$$\mathrm{Y}=10^{-2} \sin 2 \pi(160 t-0.5 x+\pi / 4)$$
where $$x$$ and $$Y$$ are in $$\mathrm{m}$$ and $$\mathrm{t}$$ in $$s$$. The speed of the wave is ________ $$\mathrm{km} ~\mathrm{h}^{-1}$$.
A transverse harmonic wave on a string is given by
$$y(x,t) = 5\sin (6t + 0.003x)$$
where x and y are in cm and t in sec. The wave velocity is _______________ ms$$^{-1}$$.
A guitar string of length 90 cm vibrates with a fundamental frequency of 120 Hz. The length of the string producing a fundamental frequency of 180 Hz will be _________ cm.
An organ pipe $$40 \mathrm{~cm}$$ long is open at both ends. The speed of sound in air is $$360 \mathrm{~ms}^{-1}$$. The frequency of the second harmonic is ___________ $$\mathrm{Hz}$$.
A person driving car at a constant speed of $$15 \mathrm{~m} / \mathrm{s}$$ is approaching a vertical wall. The person notices a change of $$40 \mathrm{~Hz}$$ in the frequency of his car's horn upon reflection from the wall. The frequency of horn is _______________ $$\mathrm{Hz}$$.
(Given: Speed of sound : $$330 \mathrm{~m} / \mathrm{s}$$ )
$y_{1}=10 \sin \left(\omega t+\frac{\pi}{3}\right) \mathrm{cm}, y_{2}=5[\sin \omega t+\sqrt{3} \cos \omega t] \mathrm{cm}$ respectively.
The amplitude of the resultant wave is _______ $\mathrm{cm}$.
Two simple harmonic waves having equal amplitudes of 8 cm and equal frequency of 10 Hz are moving along the same direction. The resultant amplitude is also 8 cm. The phase difference between the individual waves is _________ degree.
A train blowing a whistle of frequency 320 Hz approaches an observer standing on the platform at a speed of 66 m/s. The frequency observed by the observer will be (given speed of sound = 330 ms$$^{-1}$$) __________ Hz.
The distance between two consecutive points with phase difference of 60$$^\circ$$ in a wave of frequency 500 Hz is 6.0 m. The velocity with which wave is travelling is __________ km/s
The frequency of echo will be __________ Hz if the train blowing a whistle of frequency 320 Hz is moving with a velocity of 36 km/h towards a hill from which an echo is heard by the train driver. Velocity of sound in air is 330 m/s.
A wire of length 30 cm, stretched between rigid supports, has it's nth and (n + 1)th harmonics at 400 Hz and 450 Hz, respectively. If tension in the string is 2700 N, it's linear mass density is ____________ kg/m.
When a car is approaching the observer, the frequency of horn is $$100 \mathrm{~Hz}$$. After passing the observer, it is $$50 \mathrm{~Hz}$$. If the observer moves with the car, the frequency will be $$\frac{x}{3} \mathrm{~Hz}$$ where $$x=$$ ________________.
Two waves executing simple harmonic motions travelling in the same direction with same amplitude and frequency are superimposed. The resultant amplitude is equal to the $$\sqrt3$$ times of amplitude of individual motions. The phase difference between the two motions is ___________ (degree).
An observer is riding on a bicycle and moving towards a hill at $$18 \,\mathrm{kmh}^{-1}$$. He hears a sound from a source at some distance behind him directly as well as after its reflection from the hill. If the original frequency of the sound as emitted by source is $$640 \mathrm{~Hz}$$ and velocity of the sound in air is $$320 \mathrm{~m} / \mathrm{s}$$, the beat frequency between the two sounds heard by observer will be _____________ $$\mathrm{Hz}$$.
An employee of a factory moving away from his workplace by a car listens to the siren of the factory. He drives the car at the speed of 72 kmh$$-$$1 in the direction of wind which is blowing at 72 kmh$$-$$1 speed. Frequency of siren is 720 Hz. The employee hears an apparent frequency of ____________ Hz.
(Assume speed of sound to be 340 ms$$-$$1)
In an experiment to determine the velocity of sound in air at room temperature using a resonance tube, the first resonance is observed when the air column has a length of 20.0 cm for a tuning fork of frequency 400 Hz is used. The velocity of the sound at room temperature is 336 ms$$-$$1. The third resonance is observed when the air column has a length of _____________ cm.
A tunning fork of frequency 340 Hz resonates in the fundamental mode with an air column of length 125 cm in a cylindrical tube closed at one end. When water is slowly poured in it, the minimum height of water required for observing resonance once again is ___________ cm.
(Velocity of sound in air is 340 ms$$-$$1)
A set of 20 tuning forks is arranged in a series of increasing frequencies. If each fork gives 4 beats with respect to the preceding fork and the frequency of the last fork is twice the frequency of the first, then the frequency of last fork is _________ Hz.
The first overtone frequency of an open organ pipe is equal to the fundamental frequency of a closed organ pipe. If the length of the closed organ pipe is 20 cm. The length of the open organ pipe is _____________ cm.
Two travelling waves of equal amplitudes and equal frequencies move in opposite directions along a string. They interfere to produce a stationary wave whose equation is given by $$y = (10\cos \pi x\sin {{2\pi t} \over T})$$ cm
The amplitude of the particle at $$x = {4 \over 3}$$ cm will be ___________ cm.
y1 = A1 sin k(x $$-$$ vt), y2 = A2 sin k(x $$-$$ vt + x0). Given amplitudes A1 = 12 mm and A2 = 5 mm, x0 = 3.5 cm and wave number k = 6.28 cm$$-$$1. The amplitude of resulting wave will be ................ mm.
y = 1.0 mm cos(1.57 cm$$-$$1) x sin(78.5 s$$-$$1)t.
The node closest to the origin in the region x > 0 will be at x = .............. cm.