Units & Measurements · Physics · JEE Main
MCQ (Single Correct Answer)
A quantity Q is formulated as $X^{-2}Y^{+\frac{3}{2}}Z^{-\frac{2}{5}}$. X, Y, and Z are independent parameters which have fractional errors of 0.1, 0.2, and 0.5, respectively in measurement. The maximum fractional error of Q is
The dimension of $ \sqrt{\frac{\mu_0}{\epsilon_0}} $ is equal to that of:
($ \mu_0 $ = Vacuum permeability and $ \epsilon_0 $ = Vacuum permittivity)
Match List - I with List - II.
| List - I | List - II |
|---|---|
| (A) Mass density | (I) [ML2T−3] |
| (B) Impulse | (II) [MLT−1] |
| (C) Power | (III) [ML2T0] |
| (D) Moment of inertia | (IV) [ML−3T0] |
Choose the correct answer from the options given below :
In an electromagnetic system, a quantity defined as the ratio of electric dipole moment and magnetic dipole moment has dimension of $\left[\mathrm{M}^{\mathrm{P}} \mathrm{L}^{\mathrm{Q}} \mathrm{T}^R A^{\mathrm{S}}\right]$. The value of P and Q are :
For the determination of refractive index of glass slab, a travelling microscope is used whose main scale contains 300 equal divisions equals to 15 cm . The vernier scale attached to the microscope has 25 divisions equals to 24 divisions of main scale. The least count (LC) of the travelling microscope is (in cm ) :
In an electromagnetic system, the quantity representing the ratio of electric flux and magnetic flux has dimension of $M^P L^Q T^R A^S$, where value of ' $Q$ ' and ' $R$ ' are
$$ \text { Match the LIST-I with LIST-II } $$
| LIST-I |
LIST-II |
||
|---|---|---|---|
| A. | $$ \text { Boltzmann constant } $$ |
I | $$ \mathrm{ML}^2 \mathrm{~T}^{-1} $$ |
| B | $$ \text { Coefficient of viscosity } $$ |
II | $$ \mathrm{MLT}^{-3} \mathrm{~K}^{-1} $$ |
| C | $$ \text { Planck's constant } $$ |
III | $$ \mathrm{ML}^2 \mathrm{~T}^{-2} \mathrm{~K}^{-1} $$ |
| D | $$ \text { Thermal conductivity } $$ |
IV | $$ \mathrm{ML}^{-1} \mathrm{~T}^{-1} $$ |
A person measures mass of 3 different particles as $435.42 \mathrm{~g}, 226.3 \mathrm{~g}$ and 0.125 g . According to the rules for arithmetic operations with significant figures, the addition of the masses of 3 particles will be.
Match List I with List II.
| List - I | List - II | ||
|---|---|---|---|
| (A) | Coefficient of viscosity | (I) | $\left[\mathrm{ML}^0 \mathrm{~T}^{-3}\right]$ |
| (B) | Intensity of wave | (II) | $\left[\mathrm{ML}^{-2} \mathrm{~T}^{-2}\right]$ |
| (C) | Pressure gradient | (III) | $\left[\mathrm{M}^{-1} \mathrm{LT}^2\right]$ |
| (D) | Compressibility | (IV) | $\left[\mathrm{ML}^{-1} \mathrm{~T}^{-1}\right]$ |
Choose the correct answer from the options given below:
Match List - I with List - II.
| List - I | List - II |
|---|---|
| (A) Young’s Modulus | (I) M L-1 T-1 |
| (B) Torque | (II) M L-1 T-2 |
| (C) Coefficient of Viscosity | (III) M-1 L3 T-2 |
| (D) Gravitational Constant | (IV) M L2 T-2 |
Choose the correct answer from the options given below :
The pair of physical quantities not having the same dimensions is :
The expression given below shows the variation of velocity (v) with time (t),
$v=\mathrm{At}^2+\frac{\mathrm{Bt}}{\mathrm{C}+\mathrm{t}}$.
The dimension of ABC is :
Match List - I with List - II.
| List - I | List - II |
|---|---|
| (A) Angular Impulse | (I) M0 L2 T-2 |
| (B) Latent Heat | (II) M L2 T-3 A-1 |
| (C) Electrical resistivity | (III) M L2 T-1 |
| (D) Electromotive force | (IV) M L3 T-3 A-2 |
Choose the correct answer from the options given below:
For an experimental expression $y=\frac{32.3 \times 1125}{27.4}$, where all the digits are significant. Then to report the value of $y$ we should write
Match List - I with List - II
| List - I | List - II | ||
|---|---|---|---|
| (A) | Permeability of free space | (I) | $\left[\mathrm{M} \mathrm{L}^2 \mathrm{~T}^{-2}\right]$ |
| (B) | Magnetic field | (II) | $\left[\mathrm{M} \mathrm{T}^{-2} \mathrm{~A}^{-1}\right]$ |
| (C) | Magnetic moment | (III) | $\left[\mathrm{M} \mathrm{L} \mathrm{T}^{-2} \mathrm{~A}^{-2}\right]$ |
| (D) | Torsional constant | (IV) | $\left[\mathrm{L}^2 \mathrm{~A}\right]$ |
Choose the correct answer from the options given below :
The position of a particle moving on $x$-axis is given by $x(t)=A \sin t+B \cos ^2 t+C t^2+D$, where $t$ is time. The dimension of $\frac{A B C}{D}$ is
The maximum percentage error in the measurment of density of a wire is
[Given, mass of wire $=(0.60 \pm 0.003) \mathrm{g}$
radius of wire $=(0.50 \pm 0.01) \mathrm{cm}$
length of wire $=(10.00 \pm 0.05) \mathrm{cm}]$
If $B$ is magnetic field and $\mu_0$ is permeability of free space, then the dimensions of $\left(B / \mu_0\right)$ is
Given below are two statements :
Statement I: In a vernier callipers, one vernier scale division is always smaller than one main scale division.
Statement II : The vernier constant is given by one main scale division multiplied by the number of vernier scale divisions.
In the light of the above statements, choose the correct answer from the options given below.
The de-Broglie wavelength associated with a particle of mass $$m$$ and energy $$E$$ is $$h / \sqrt{2 m E}$$. The dimensional formula for Planck's constant is :
The dimensional formula of latent heat is :
One main scale division of a vernier caliper is equal to $$\mathrm{m}$$ units. If $$\mathrm{n}^{\text {th }}$$ division of main scale coincides with $$(n+1)^{\text {th }}$$ division of vernier scale, the least count of the vernier caliper is :
If $$\epsilon_{\mathrm{o}}$$ is the permittivity of free space and $$\mathrm{E}$$ is the electric field, then $$\epsilon_{\mathrm{o}} \mathrm{E}^2$$ has the dimensions :
There are 100 divisions on the circular scale of a screw gauge of pitch $$1 \mathrm{~mm}$$. With no measuring quantity in between the jaws, the zero of the circular scale lies 5 divisions below the reference line. The diameter of a wire is then measured using this screw gauge. It is found that 4 linear scale divisions are clearly visible while 60 divisions on circular scale coincide with the reference line. The diameter of the wire is :
Least count of a vernier caliper is $$\frac{1}{20 \mathrm{~N}} \mathrm{~cm}$$. The value of one division on the main scale is $$1 \mathrm{~mm}$$. Then the number of divisions of main scale that coincide with $$\mathrm{N}$$ divisions of vernier scale is :
In an expression $$a \times 10^b$$ :
The diameter of a sphere is measured using a vernier caliper whose 9 divisions of main scale are equal to 10 divisions of vernier scale. The shortest division on the main scale is equal to $$1 \mathrm{~mm}$$. The main scale reading is $$2 \mathrm{~cm}$$ and second division of vernier scale coincides with a division on main scale. If mass of the sphere is 8.635 $$\mathrm{g}$$, the density of the sphere is:
In a vernier calliper, when both jaws touch each other, zero of the vernier scale shifts towards left and its $$4^{\text {th }}$$ division coincides exactly with a certain division on main scale. If 50 vernier scale divisions equal to 49 main scale divisions and zero error in the instrument is $$0.04 \mathrm{~mm}$$ then how many main scale divisions are there in $$1 \mathrm{~cm}$$ ?
In finding out refractive index of glass slab the following observations were made through travelling microscope 50 vernier scale division $$=49 \mathrm{~MSD} ; 20$$ divisions on main scale in each $$\mathrm{cm}$$
For mark on paper
$$\text { MSR }=8.45 \mathrm{~cm}, \mathrm{VC}=26$$
For mark on paper seen through slab
$$\mathrm{MSR}=7.12 \mathrm{~cm}, \mathrm{VC}=41$$
For powder particle on the top surface of the glass slab
$$\text { MSR }=4.05 \mathrm{~cm}, \mathrm{VC}=1$$
(MSR $$=$$ Main Scale Reading, VC = Vernier Coincidence)
Refractive index of the glass slab is :
To find the spring constant $$(k)$$ of a spring experimentally, a student commits $$2 \%$$ positive error in the measurement of time and $$1 \%$$ negative error in measurement of mass. The percentage error in determining value of $$k$$ is :
Match List I with List II
| LIST I | LIST II | ||
|---|---|---|---|
| A. | Torque | I. | $$ \left[M^1 L^1 T^{-2} A^{-2}\right] $$ |
| B. | Magnetic field | II. | $$ \left[L^2 A^1\right] $$ |
| C. | Magnetic moment | III. | $$ \left[M^1 T^{-2} A^{-1}\right] $$ |
| D. | Permeability of free space | IV. | $$ \left[M^1 L^2 T^{-2}\right] $$ |
Choose the correct answer from the options given below:
While measuring diameter of wire using screw gauge the following readings were noted. Main scale reading is $$1 \mathrm{~mm}$$ and circular scale reading is equal to 42 divisions. Pitch of screw gauge is $$1 \mathrm{~mm}$$ and it has 100 divisions on circular scale. The diameter of the wire is $$\frac{x}{50} \mathrm{~mm}$$. The value of $$x$$ is :
What is the dimensional formula of $$a b^{-1}$$ in the equation $$\left(\mathrm{P}+\frac{\mathrm{a}}{\mathrm{V}^2}\right)(\mathrm{V}-\mathrm{b})=\mathrm{RT}$$, where letters have their usual meaning.
A vernier callipers has 20 divisions on the vernier scale, which coincides with $$19^{\text {th }}$$ division on the main scale. The least count of the instrument is $$0.1 \mathrm{~mm}$$. One main scale division is equal to ________ mm.
Time periods of oscillation of the same simple pendulum measured using four different measuring clocks were recorded as $$4.62 \mathrm{~s}, 4.632 \mathrm{~s}, 4.6 \mathrm{~s}$$ and $$4.64 \mathrm{~s}$$. The arithmetic mean of these readings in correct significant figure is :
Applying the principle of homogeneity of dimensions, determine which one is correct, where $$T$$ is time period, $$G$$ is gravitational constant, $$M$$ is mass, $$r$$ is radius of orbit.
The equation of stationary wave is :
$$y=2 \mathrm{a} \sin \left(\frac{2 \pi \mathrm{nt}}{\lambda}\right) \cos \left(\frac{2 \pi x}{\lambda}\right) \text {. }$$
Which of the following is NOT correct :
| List I (Number) | List II (Significant figure) |
|---|---|
| (A) 1001 | (I) 3 |
| (B) 010.1 | (II) 4 |
| (C) 100.100 | (III) 5 |
| (D) 0.0010010 | (IV) 6 |
Choose the correct answer from the options given below :
$$ \begin{aligned} & \mathrm{r}=(0.35 \pm 0.05) ~\mathrm{cm} \\\\ & \mathrm{R}=(100 \pm 10) ~\mathrm{ohm} \\\\ & l=(15 \pm 0.2)~ \mathrm{cm} \end{aligned} $$
The percentage error in resistivity of the material of the wire is :
Consider two physical quantities $$A$$ and $$B$$ related to each other as $$E=\frac{B-x^2}{A t}$$ where $$E, x$$ and $$t$$ have dimensions of energy, length and time respectively. The dimension of $$A B$$ is
The measured value of the length of a simple pendulum is $$20 \mathrm{~cm}$$ with $$2 \mathrm{~mm}$$ accuracy. The time for 50 oscillations was measured to be 40 seconds with 1 second resolution. From these measurements, the accuracy in the measurement of acceleration due to gravity is $$\mathrm{N} \%$$. The value of $$\mathrm{N}$$ is:
If the percentage errors in measuring the length and the diameter of a wire are $$0.1 \%$$ each. The percentage error in measuring its resistance will be:
A force is represented by $$F=a x^2+b t^{\frac{1}{2}}$$
where $$x=$$ distance and $$t=$$ time. The dimensions of $$b^2 / a$$ are:
If 50 Vernier divisions are equal to 49 main scale divisions of a traveling microscope and one smallest reading of main scale is $$0.5 \mathrm{~mm}$$, the Vernier constant of traveling microscope is
If mass is written as $$m=k \mathrm{c}^{\mathrm{P}} G^{-1 / 2} h^{1 / 2}$$ then the value of $$P$$ will be : (Constants have their usual meaning with $k a$ dimensionless constant)
Match List I with List II.
| List I | List II | ||
|---|---|---|---|
| (A) | Coefficient of viscosity | (I) | $$\left[\mathrm{M} \mathrm{L}^2 \mathrm{~T}^{-2}\right]$$ |
| (B) | Surface tension | (II) | $$\left[\mathrm{M} \mathrm{L}^2 \mathrm{~T}^{-1}\right]$$ |
| (C) | Angular momentum | (III) | $$\left[\mathrm{M} \mathrm{L}^{-1} \mathrm{~T}^{-1}\right]$$ |
| (D) | Rotational kinetic energy | (IV) | $$\left[\mathrm{M} \mathrm{L}^0 \mathrm{~T}^{-2}\right]$$ |
Choose the correct answer from the options given below :
A physical quantity $$Q$$ is found to depend on quantities $$a, b, c$$ by the relation $$Q=\frac{a^4 b^3}{c^2}$$. The percentage error in $$a, b$$ and $$c$$ are $$3 \%, 4 \%$$ and $$5 \%$$ respectively. Then, the percentage error in $$Q$$ is :
The resistance $$R=\frac{V}{I}$$ where $$\mathrm{V}=(200 \pm 5) \mathrm{V}$$ and $$I=(20 \pm 0.2) \mathrm{A}$$, the percentage error in the measurement of $$\mathrm{R}$$ is :
Given below are two statements : one is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : In Vernier calliper if positive zero error exists, then while taking measurements, the reading taken will be more than the actual reading.
Reason (R) : The zero error in Vernier Calliper might have happened due to manufacturing defect or due to rough handling.
In the light of the above statements, choose the correct answer from the options given below :
Given below are two statements :
Statement (I) : Planck's constant and angular momentum have same dimensions.
Statement (II) : Linear momentum and moment of force have same dimensions.
In the light of the above statements, choose the correct answer from the options given below :
In the equation $$\left[X+\frac{a}{Y^{2}}\right][Y-b]=\mathrm{R} T, X$$ is pressure, $$Y$$ is volume, $$\mathrm{R}$$ is universal gas constant and $$T$$ is temperature. The physical quantity equivalent to the ratio $$\frac{a}{b}$$ is:
A body of mass $$(5 \pm 0.5) ~\mathrm{kg}$$ is moving with a velocity of $$(20 \pm 0.4) ~\mathrm{m} / \mathrm{s}$$. Its kinetic energy will be
Match List I with List II
| LIST I | LIST II | ||
|---|---|---|---|
| A. | Spring constant | I. | $$\mathrm{[T^{-1}]}$$ |
| B. | Angular speed | II. | $$\mathrm{[MT^{-2}]}$$ |
| C. | Angular momentum | III. | $$\mathrm{[ML^2]}$$ |
| D. | Moment of inertia | IV. | $$\mathrm{[ML^2T^{-1}]}$$ |
Choose the correct answer from the options given below:
If force (F), velocity (V) and time (T) are considered as fundamental physical quantity, then dimensional formula of density will be :
Given below are two statements :
Statements I : Astronomical unit (Au), Parsec (Pc) and Light year (ly) are units for measuring astronomical distances.
Statements II : $$\mathrm{Au} < \mathrm{Parsec} (\mathrm{Pc}) < \mathrm{ly}$$
In the light of the above statements, choose the most appropriate answer from the options given below:
In an experiment with vernier callipers of least count $$0.1 \mathrm{~mm}$$, when two jaws are joined together the zero of vernier scale lies right to the zero of the main scale and 6th division of vernier scale coincides with the main scale division. While measuring the diameter of a spherical bob, the zero of vernier scale lies in between $$3.2 \mathrm{~cm}$$ and $$3.3 \mathrm{~cm}$$ marks, and 4th division of vernier scale coincides with the main scale division. The diameter of bob is measured as
A physical quantity P is given as
$$P = {{{a^2}{b^3}} \over {c\sqrt d }}$$
The percentage error in the measurement of a, b, c and d are 1%, 2%, 3% and 4% respectively. The percentage error in the measurement of quantity P will be
Match List I with List II
| LIST I | LIST II | ||
|---|---|---|---|
| A. | Torque | I. | $$\mathrm{ML^{-2}T^{-2}}$$ |
| B. | Stress | II. | $$\mathrm{ML^2T^{-2}}$$ |
| C. | Pressure gradient | III. | $$\mathrm{ML^{-1}T^{-1}}$$ |
| D. | Coefficient of viscosity | IV. | $$\mathrm{ML^{-1}T^{-2}}$$ |
Choose the correct answer from the options given below:
Dimension of $$\frac{1}{\mu_{0} \in_{0}}$$ should be equal to
A cylindrical wire of mass $$(0.4 \pm 0.01) \mathrm{g}$$ has length $$(8 \pm 0.04) \mathrm{cm}$$ and radius $$(6 \pm 0.03) \mathrm{mm}$$. The maximum error in its density will be:
Two resistances are given as $$\mathrm{R}_{1}=(10 \pm 0.5) \Omega$$ and $$\mathrm{R}_{2}=(15 \pm 0.5) \Omega$$. The percentage error in the measurement of equivalent resistance when they are connected in parallel is -
If the velocity of light $$\mathrm{c}$$, universal gravitational constant $$\mathrm{G}$$ and Planck's constant $$\mathrm{h}$$ are chosen as fundamental quantities. The dimensions of mass in the new system is :
| LIST I | LIST II | ||
|---|---|---|---|
| A. | Angular momentum | I. | $\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]$ |
| B. | Torque | II. | $\left[\mathrm{ML}^{-2} \mathrm{~T}^{-2}\right]$ |
| C. | Stress | III | $\left[\mathrm{ML}^{2} \mathrm{~T}^{-1}\right]$ |
| D. | Pressure gradient | IV. | $\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]$ |
Choose the correct answer from the options given below:
Match List I with List II:
| List I | List II | ||
|---|---|---|---|
| A. | Torque | I. | $\mathrm{kg} \mathrm{m}^{-1} \mathrm{~s}^{-2}$ |
| B. | Energy density | II. | $\mathrm{kg} \,\mathrm{ms}^{-1}$ |
| C. | Pressure gradient | III. | $\mathrm{kg}\, \mathrm{m}^{-2} \mathrm{~s}^{-2}$ |
| D. | Impulse | IV. | $\mathrm{kg} \,\mathrm{m}^{2} \mathrm{~s}^{-2}$ |
Choose the correct answer from the options given below:
The equation of a circle is given by $$x^2+y^2=a^2$$, where a is the radius. If the equation is modified to change the origin other than (0, 0), then find out the correct dimensions of A and B in a new equation : $${(x - At)^2} + {\left( {y - {t \over B}} \right)^2} = {a^2}$$. The dimensions of t is given as $$[\mathrm{T^{-1}]}$$.
Match List I with List II :
| List I (Physical Quantity) | List II (Dimensional Formula) | ||
|---|---|---|---|
| A. | Pressure gradient | I. | $$\left[\mathrm{M}^{\circ} \mathrm{L}^{2} \mathrm{~T}^{-2}\right]$$ |
| B. | Energy density | II. | $$\left[\mathrm{M}^{1} \mathrm{L}^{-1} \mathrm{~T}^{-2}\right]$$ |
| C. | Electric Field | III. | $$\left[\mathrm{M}^{1} \mathrm{L}^{-2} \mathrm{~T}^{-2}\right]$$ |
| D. | Latent heat | IV. | $$\left[\mathrm{M}^{1} \mathrm{~L}^{1} \mathrm{~T}^{-3} \mathrm{~A}^{-1}\right]$$ |
Choose the correct answer from the options given below:
Match List I with List II
| List I | List II | ||
|---|---|---|---|
| A. | Young's Modulus (Y) | I. | $$\mathrm{[ML^{-1}T^{-1}]}$$ |
| B. | Co-efficient of Viscosity ($$\eta$$) | II. | $$\mathrm{[ML^2T^{-1}]}$$ |
| C. | Planck's Constant (h) | III. | $$\mathrm{[ML^{-1}T^{-2}]}$$ |
| D. | Work function ($$\varphi $$) | IV. | $$\mathrm{[ML^2T^{-2}]}$$ |
Choose the correct answer from the options given below :
Match List I with List II
| List-I |
List-II |
||
|---|---|---|---|
| A. | Planck's constant (h) | I. | $$\mathrm{[{M^1}\,{L^2}\,{T^{ - 2}}]}$$ |
| B. | Stopping potential (Vs) | II. | $$\mathrm{[{M^1}\,{L^1}\,{T^{ - 1}}]}$$ |
| C. | Work function ($$\phi$$) | III. | $$\mathrm{[{M^1}\,{L^2}\,{T^{ - 1}}]}$$ |
| D. | Momentum (p) | IV. | $$\mathrm{[{M^1}\,{L^2}\,{T^{ - 3}}\,{A^{ - 1}}]}$$ |
Choose the correct answer from the options given below :
Match List I with List II.
| List I | List II | ||
|---|---|---|---|
| A. | Torque | I. | Nms$$^{ - 1}$$ |
| B. | Stress | II. | J kg$$^{ - 1}$$ |
| C. | Latent Heat | III. | Nm |
| D. | Power | IV. | Nm$$^{ - 2}$$ |
Choose the correct answer from the options given below :
Given below are two statements : One is labelled as Assertion (A) and other is labelled as Reason (R).
Assertion (A) : Time period of oscillation of a liquid drop depends on surface tension (S), if density of the liquid is $$\rho$$ and radius of the drop is r, then $$\mathrm{T}=\mathrm{K} \sqrt{\rho \mathrm{r}^{3} / \mathrm{S}^{3 / 2}}$$ is dimensionally correct, where K is dimensionless.
Reason (R) : Using dimensional analysis we get R.H.S. having different dimension than that of time period.
In the light of above statements, choose the correct answer from the options given below.
A travelling microscope has 20 divisions per $$\mathrm{cm}$$ on the main scale while its vernier scale has total 50 divisions and 25 vernier scale divisions are equal to 24 main scale divisions, what is the least count of the travelling microscope?
In an experiment to find out the diameter of wire using screw gauge, the following observations were noted :

(A) Screw moves $$0.5 \mathrm{~mm}$$ on main scale in one complete rotation
(B) Total divisions on circular scale $$=50$$
(C) Main scale reading is $$2.5 \mathrm{~mm}$$
(D) $$45^{\text {th }}$$ division of circular scale is in the pitch line
(E) Instrument has 0.03 mm negative error
Then the diameter of wire is :
Consider the efficiency of carnot's engine is given by $$\eta=\frac{\alpha \beta}{\sin \theta} \log_e \frac{\beta x}{k T}$$, where $$\alpha$$ and $$\beta$$ are constants. If T is temperature, k is Boltzmann constant, $$\theta$$ is angular displacement and x has the dimensions of length. Then, choose the incorrect option :
The dimensions of $$\left(\frac{\mathrm{B}^{2}}{\mu_{0}}\right)$$ will be :
(if $$\mu_{0}$$ : permeability of free space and $$B$$ : magnetic field)
An expression of energy density is given by $$u=\frac{\alpha}{\beta} \sin \left(\frac{\alpha x}{k t}\right)$$, where $$\alpha, \beta$$ are constants, $$x$$ is displacement, $$k$$ is Boltzmann constant and t is the temperature. The dimensions of $$\beta$$ will be :
A torque meter is calibrated to reference standards of mass, length and time each with $$5 \%$$ accuracy. After calibration, the measured torque with this torque meter will have net accuracy of :
In a Vernier Calipers, 10 divisions of Vernier scale is equal to the 9 divisions of main scale. When both jaws of Vernier calipers touch each other, the zero of the Vernier scale is shifted to the left of zero of the main scale and $$4^{\text {th }}$$ Vernier scale division exactly coincides with the main scale reading. One main scale division is equal to $$1 \mathrm{~mm}$$. While measuring diameter of a spherical body, the body is held between two jaws. It is now observed that zero of the Vernier scale lies between 30 and 31 divisions of main scale reading and $$6^{\text {th }}$$ Vernier scale division exactly coincides with the main scale reading. The diameter of the spherical body will be :
A screw gauge of pitch $$0.5 \mathrm{~mm}$$ is used to measure the diameter of uniform wire of length $$6.8 \mathrm{~cm}$$, the main scale reading is $$1.5 \mathrm{~mm}$$ and circular scale reading is 7 . The calculated curved surface area of wire to appropriate significant figures is :
[Screw gauge has 50 divisions on its circular scale]
The maximum error in the measurement of resistance, current and time for which current flows in an electrical circuit are $$1 \%, 2 \%$$ and $$3 \%$$ respectively. The maximum percentage error in the detection of the dissipated heat will be :
If momentum [P], area $$[\mathrm{A}]$$ and time $$[\mathrm{T}]$$ are taken as fundamental quantities, then the dimensional formula for coefficient of viscosity is :
If n main scale divisions coincide with (n + 1) vernier scale divisions. The least count of vernier callipers, when each centimetre on the main scale is divided into five equal parts, will be :
Velocity (v) and acceleration (a) in two systems of units 1 and 2 are related as $${v_2} = {n \over {{m^2}}}{v_1}$$ and $${a_2} = {{{a_1}} \over {mn}}$$ respectively. Here m and n are constants. The relations for distance and time in two systems respectively are :
The SI unit of a physical quantity is pascal-second. The dimensional formula of this quantity will be :
A silver wire has a mass (0.6 $$\pm$$ 0.006) g, radius (0.5 $$\pm$$ 0.005) mm and length (4 $$\pm$$ 0.04) cm. The maximum percentage error in the measurement of its density will be :
The dimension of mutual inductance is :
An expression for a dimensionless quantity P is given by $$P = {\alpha \over \beta }{\log _e}\left( {{{kt} \over {\beta x}}} \right)$$; where $$\alpha$$ and $$\beta$$ are constants, x is distance; k is Boltzmann constant and t is the temperature. Then the dimensions of $$\alpha$$ will be :
If $$Z = {{{A^2}{B^3}} \over {{C^4}}}$$, then the relative error in Z will be :
Identify the pair of physical quantities that have same dimensions:
Identify the pair of physical quantities which have different dimensions:
| Physical Quantity |
Least count of the Equipment used for measurement |
Observed value |
|---|---|---|
| Mass (M) | 1 g | 2 kg |
| Length of bar (L) | 1 mm | 1 m |
| Breadth of bar (b) | 0.1 mm | 4 cm |
| Thickness of bar (d) | 0.01 mm | 0.4 cm |
| Depression ($$\delta $$) | 0.01 mm | 5 mm |
Then the fractional error in the measurement of Y is :
| List - I | List - II | ||
|---|---|---|---|
| (a) | Torque | (i) | MLT$$^{ - 1}$$ |
| (b) | Impulse | (ii) | MT$$^{ - 2}$$ |
| (c) | Tension | (iii) | ML$$^{ 2}$$T$$^{ - 2}$$ |
| (d) | Surface Tension | (iv) | MLT$$^{ - 2}$$ |
Choose the most appropriate answer from the option given below :
Where t = time, h = height, s = surface tension, $$\theta$$ = angle, $$\rho$$ = density, a, r = radius, g = acceleration due to gravity, v = volume, p = pressure, W = work done, T = torque, $$\in$$ = permittivity, E = electric field, J = current density, L = length.
| List - I | List - II | ||
|---|---|---|---|
| (a) | $${R_H}$$ (Rydberg constant) | (i) | $$kg\,{m^{ - 1}}{s^{ - 1}}$$ |
| (b) | h (Planck's constant) | (ii) | $$kg\,{m^2}{s^{ - 1}}$$ |
| (c) | $${\mu _B}$$ (Magnetic field energy density) | (iii) | $$\,{m^{ - 1}}$$ |
| (d) | $$\eta $$ (coefficient of viscocity) | (iv) | $$kg\,{m^{ - 1}}{s^{ - 2}}$$ |
Choose the most appropriate answer from the options given below :

Choose the most appropriate answer from the options given below :
If the percentage errors found in y, m, r, l and g are 18, 1, 0.5, 4 and p respectively, then find the value of x and p.
Reason R :
Least Count = $${{Pitch} \over {Total\,divisions\,on\,circular\,scale}}$$
In the light of the above statements, choose the most appropriate answer from the options given below :
F = A cos Bx + C sin Dt
The dimensional formula of $${{AD} \over B}$$ is :
| List I | List II | ||
|---|---|---|---|
| (a) | h (Planck's constant) | (i) | $$[ML{T^{ - 1}}]$$ |
| (b) | E (kinetic energy) | (ii) | $$[M{L^2}{T^{ - 1}}]$$ |
| (c) | V (electric potential) | (iii) | $$[M{L^2}{T^{ - 2}}]$$ |
| (d) | P (linear momentum) | (iv) | $$[M{L^2}{I^{ - 1}}{T^{ - 3}}]$$ |
Choose the correct answer from the options given below :
given by, $$W = \alpha {\beta ^2}{e^{ - {{{x^2}} \over {\alpha kT}}}}$$, where x is the displacement, k is the Boltzmann constant and T is the temperature. $$\alpha$$ and $$\beta$$ are constants. Then the dimensions of $$\beta$$ will be :
of the pencil should therefore be recorded as :
defined where C-capacitance, R-Resistance, l-length, E-Electric field, B-magnetic field and $${{\varepsilon _0}}$$, $${{\mu _0}}$$, - free space permittivity and permeability respectively. Then :
a, b, c and d, as z = $${{{a^2}{b^{{2 \over 3}}}} \over {\sqrt c {d^3}}}$$. The percentages of error in the measurement of a, b, c and d are 2%, 1.5%, 4% and 2.5% respectively. The percentage of error in z is :
(i) A1 = 24.36, B1 = 0.0724, C1 = 256.2
(ii) A2 = 24.44, B2 = 16.082, C2 = 240.2
(iii) A3 = 25.2, B3 = 19.2812, C3 = 236.183
(iv) A4 = 25, B4 = 236.191, C4 = 19.5
The readings of the main scale and the circular scale, for a thin sheet, are 5.5 mm and 48 respectively, the thickness of this sheet is :
The maximum percentage error in the value of A will be :
Which of the following correctly gives the Planck length ?
P = a$$^{{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}$$ b2 c3 d$$-$$4
If the relative errors in the measurement of a, b, c and d respectively, are 2%, 1%, 3% and 5%, then the relative error in P will be :
diameter of capillary, D = 1.25 $$\times$$ 10-2 m
rise of water, h = 1.45 $$\times$$ 10-2m
Using g = 9.80 m/s2 and the simplified relation T = $${{rhg} \over 2} \times {10^3}N/m$$, the possible error in surface tension is closest to :
Main scale reading: 58.5 degree
Vernier scale reading : 09 divisions
Given that 1 division on main scale corresponds to 0.5 degree. Total divisions on the vernier scale is 30 and match with 29 divisions of the main scale. The angle of the prism from the above data
Main scale reading : 0 mm
Circular scale reading : 52 divisions
Given that 1 mm on main scale corresponds to 100 divisions of the circular scale.
The diameter of wire from the above date is:
Numerical
A physical quantity C is related to four other quantities $\mathrm{p}, \mathrm{q}, \mathrm{r}$ and s as follows
$$ C=\frac{p q^2}{r^3 \sqrt{s}} $$
The percentage errors in the measurement of $\mathrm{p}, \mathrm{q}, \mathrm{r}$ and s are $1 \%, 2 \%, 3 \%$ and $2 \%$, respectively. The percentage error in the measurement of $C$ will be__________%
$\text { A physical quantity } Q \text { is related to four observables } a, b, c, d \text { as follows : }$
$Q = \frac{ab^4}{cd}$
where, $\mathrm{a}=(60 \pm 3) \mathrm{Pa} ; \mathrm{b}=(20 \pm 0.1) \mathrm{m} ; \mathrm{c}=(40 \pm 0.2) \mathrm{Nsm}^{-2}$ and $\mathrm{d}=(50 \pm 0.1) \mathrm{m}$, then the percentage error in Q is $\frac{x}{1000}$, where $x=$ _________ .
A tiny metallic rectangular sheet has length and breadth of 5 mm and 2.5 mm , respectively. Using a specially designed screw gauge which has pitch of 0.75 mm and 15 divisions in the circular scale, you are asked to find the area of the sheet. In this measurement, the maximum fractional error will be $\frac{x}{100}$ where $x$ is _______ .
The least count of a screw guage is 0.01 mm . If the pitch is increased by $75 \%$ and number of divisions on the circular scale is reduced by $50 \%$, the new least count will be ________ $\times 10^{-3} \mathrm{~mm}$
In a screw gauge, there are 100 divisions on the circular scale and the main scale moves by $$0.5 \mathrm{~mm}$$ on a complete rotation of the circular scale. The zero of circular scale lies 6 divisions below the line of graduation when two studs are brought in contact with each other. When a wire is placed between the studs, 4 linear scale divisions are clearly visible while $$46^{\text {th }}$$ division the circular scale coincide with the reference line. The diameter of the wire is ______________ $$\times 10^{-2} \mathrm{~mm}$$.
In an experiment to find acceleration due to gravity (g) using simple pendulum, time period of $$0.5 \mathrm{~s}$$ is measured from time of 100 oscillation with a watch of $$1 \mathrm{~s}$$ resolution. If measured value of length is $$10 \mathrm{~cm}$$ known to $$1 \mathrm{~mm}$$ accuracy, The accuracy in the determination of $$\mathrm{g}$$ is found to be $$x \%$$. The value of $$x$$ is ___________.
The one division of main scale of Vernier callipers reads $$1 \mathrm{~mm}$$ and 10 divisions of Vernier scale is equal to the 9 divisions on main scale. When the two jaws of the instrument touch each other, the zero of the Vernier lies to the right of zero of the main scale and its fourth division coincides with a main scale division. When a spherical bob is tightly placed between the two jaws, the zero of the Vernier scale lies in between $$4.1 \mathrm{~cm}$$ and $$4.2 \mathrm{~cm}$$ and $$6^{\text {th }}$$ Vernier division coincides scale division. The diameter of the bob will be ____________ $$\times$$ 10$$-$$2 cm.
The Vernier constant of Vernier callipers is 0.1 mm and it has zero error of ($$-$$0.05) cm. While measuring diameter of a sphere, the main scale reading is 1.7 cm and coinciding vernier division is 5. The corrected diameter will be _________ $$\times$$ 10$$-$$2 cm.
A student in the laboratory measures thickness of a wire using screw gauge. The readings are 1.22 mm, 1.23 mm, 1.19 mm and 1.20 mm. The percentage error is $${x \over {121}}\% $$. The value of x is ____________.
A travelling microscope is used to determine the refractive index of a glass slab. If 40 divisions are there in 1 cm on main scale and 50 Vernier scale divisions are equal to 49 main scale divisions, then least count of the travelling microscope is __________ $$\times$$ 10$$-$$6 m.
In a vernier callipers, each cm on the main scale is divided into 20 equal parts. If tenth vernier scale division coincides with nineth main scale division. Then the value of vernier constant will be _________ $$\times$$ 10$$-$$2 mm.
For $$z = {a^2}{x^3}{y^{{1 \over 2}}}$$, where 'a' is a constant. If percentage error in measurement of 'x' and 'y' are 4% and 12% respectively, then the percentage error for 'z' will be _______________%.
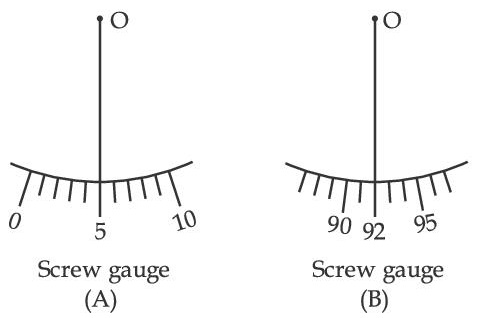
[Figure shows position of reference 'O' when jaws of screw gauge are closed]
Given pitch = 0.1 cm.
| Student No. |
Length of Pendulum (cm) |
No. of oscillations (n) |
Total time for n oscillations |
Time period (s) |
|---|---|---|---|---|
| 1 | 64.0 | 8 | 128.0 | 16.0 |
| 2 | 64.0 | 4 | 64.0 | 16.0 |
| 3 | 20.0 | 4 | 36.0 | 9.0 |
(Least count of length = 0.1 cm and Least count for time = 0.1 s)
If E1, E2 and E3 are the percentage errors in 'g' for students 1, 2 and 3 respectively, then the minimum percentage error is obtained by student no. ______________.
The value of x, to the nearest x, is __________.