Simple Harmonic Motion · Physics · JEE Main
MCQ (Single Correct Answer)
A block of mass 2 kg is attached to one end of a massless spring whose other end is fixed at a wall. The spring-mass system moves on a frictionless horizontal table. The spring's natural length is 2 m and spring constant is 200 N/m. The block is pushed such that the length of the spring becomes 1 m and then released. At distance x m (x < 2) from the wall, the speed of the block will be
Two simple pendulums having lengths $l_1$ and $l_2$ with negligible string mass undergo angular displacements $\theta_1$ and $\theta_2$, from their mean positions, respectively. If the angular accelerations of both pendulums are same, then which expression is correct?

Two blocks of masses $m$ and $M,(M>m)$, are placed on a frictionless table as shown in figure. A massless spring with spring constant k is attached with the lower block. If the system is slightly displaced and released, then ( $\mu=$ coefficient of friction between the two blocks)
A. The time period of small oscillation of the two blocks is $T=2 \pi \sqrt{\frac{(m+M)}{k}}$
B. The acceleration of the blocks is $a=-\frac{k x}{M+m}$ ( $x=$ displacement of the blocks from the mean position)
C. The magnitude of the frictional force on the upper block is $\frac{m \mu|x|}{M+m}$
D. The maximum amplitude of the upper block, if it does not slip, is $\frac{\mu(M+m) g}{k}$
E. Maximum frictional force can be $\mu(\mathrm{M}+\mathrm{m}) \mathrm{g}$.
Choose the correct answer from the options given below :
A particle is subjected to two simple harmonic motions as : $$ x_1=\sqrt{7} \sin 5 \mathrm{tcm} $$ and $x_2=2 \sqrt{7} \sin \left(5 t+\frac{\pi}{3}\right) \mathrm{cm}$ where $x$ is displacement and $t$ is time in seconds. The maximum acceleration of the particle is $x \times 10^{-2} \mathrm{~ms}^{-2}$. The value of $x$ is :
Two bodies A and B of equal mass are suspended from two massless springs of spring constant k1 and k2, respectively. If the bodies oscillate vertically such that their amplitudes are equal, the ratio of the maximum velocity of A to the maximum velocity of B is
Given below are two statements: one is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : Time period of a simple pendulum is longer at the top of a mountain than that at the base of the mountain.
Reason (R) : Time period of a simple pendulum decreases with increasing value of acceleration due to gravity and vice-versa.
In the light of the above statements, choose the most appropriate answer from the options given below :
Given below are two statements. One is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : Knowing initial position $\mathrm{x}_0$ and initial momentum $p_0$ is enough to determine the position and momentum at any time $t$ for a simple harmonic motion with a given angular frequency $\omega$.
Reason (R) : The amplitude and phase can be expressed in terms of $\mathrm{X}_0$ an $\mathrm{p}_0$.
In the light of the above statements, choose the correct answer from the options given below :
A particle oscillates along the $x$-axis according to the law, $x(\mathrm{t})=x_0 \sin ^2\left(\frac{\mathrm{t}}{2}\right)$ where $x_0=1 \mathrm{~m}$. The kinetic energy $(\mathrm{K})$ of the particle as a function of $x$ is correctly represented by the graph
A light hollow cube of side length 10 cm and mass 10 g , is floating in water. It is pushed down and released to execute simple harmonic oscillations. The time period of oscillations is $y \pi \times 10^{-2} \mathrm{~s}$, where the value of $y$ is (Acceleration due to gravity, $g=10 \mathrm{~m} / \mathrm{s}^2$, density of water $=10^3 \mathrm{~kg} / \mathrm{m}^3$ )
Given below are two statements. One is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : A simple pendulum is taken to a planet of mass and radius, 4 times and 2 times, respectively, than the Earth. The time period of the pendulum remains same on earth and the planet.
Reason (R) : The mass of the pendulum remains unchanged at Earth and the other planet.
In the light of the above statements, choose the correct answer from the options given below :
A simple pendulum doing small oscillations at a place $$R$$ height above earth surface has time period of $$T_1=4 \mathrm{~s}$$. $$\mathrm{T}_2$$ would be it's time period if it is brought to a point which is at a height $$2 \mathrm{R}$$ from earth surface. Choose the correct relation [$$\mathrm{R}=$$ radius of earth] :
In simple harmonic motion, the total mechanical energy of given system is $$E$$. If mass of oscillating particle $$P$$ is doubled then the new energy of the system for same amplitude is:

The bob of a pendulum was released from a horizontal position. The length of the pendulum is $$10 \mathrm{~m}$$. If it dissipates $$10 \%$$ of its initial energy against air resistance, the speed with which the bob arrives at the lowest point is:
[Use, $$\mathrm{g}: 10 \mathrm{~ms}^{-2}$$]
(A) Restoring force is directly proportional to the displacement.
(B) The acceleration and displacement are opposite in direction.
(C) The velocity is maximum at mean position.
(D) The acceleration is minimum at extreme points.
Choose the correct answer from the options given below:
A particle executes SHM of amplitude A. The distance from the mean position when its's kinetic energy becomes equal to its potential energy is :
Which graph represents the difference between total energy and potential energy of a particle executing SHM vs it's distance from mean position ?
A particle is executing simple harmonic motion (SHM). The ratio of potential energy and kinetic energy of the particle when its displacement is half of its amplitude will be
The variation of kinetic energy (KE) of a particle executing simple harmonic motion with the displacement $$(x)$$ starting from mean position to extreme position (A) is given by
A particle executes S.H.M. of amplitude A along x-axis. At t = 0, the position of the particle is $$x=\frac{A}{2}$$ and it moves along positive x-axis. The displacement of particle in time t is $$x = A\sin (wt + \delta )$$, then the value of $$\delta$$ will be
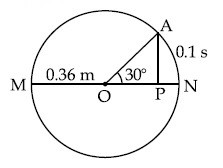
For particle P revolving round the centre O with radius of circular path $$\mathrm{r}$$ and angular velocity $$\omega$$, as shown in below figure, the projection of OP on the $$x$$-axis at time $$t$$ is

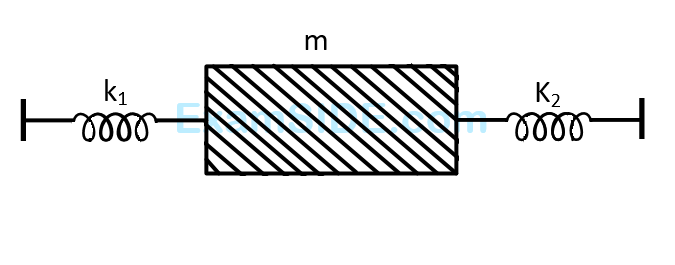
A mass $$m$$ is attached to two strings as shown in figure. The spring constants of two springs are $$\mathrm{K}_{1}$$ and $$\mathrm{K}_{2}$$. For the frictionless surface, the time period of oscillation of mass $$m$$ is :

Choose the correct length (L) versus square of the time period ($$\mathrm{T}^{2}$$) graph for a simple pendulum executing simple harmonic motion.
The maximum potential energy of a block executing simple harmonic motion is $$25 \mathrm{~J}$$. A is amplitude of oscillation. At $$\mathrm{A / 2}$$, the kinetic energy of the block is
For a simple harmonic motion in a mass spring system shown, the surface is frictionless. When the mass of the block is $1 \mathrm{~kg}$, the angular frequency is $\omega_{1}$. When the mass block is $2 \mathrm{~kg}$ the angular frequency is $\omega_{2}$. The ratio $\omega_{2} / \omega_{1}$ is

A particle executes simple harmonic motion between $$x=-A$$ and $$x=+A$$. If time taken by particle to go from $$x=0$$ to $$\frac{A}{2}$$ is 2 s; then time taken by particle in going from $$x=\frac{A}{2}$$ to A is
T is the time period of simple pendulum on the earth's surface. Its time period becomes $$x$$ T when taken to a height R (equal to earth's radius) above the earth's surface. Then, the value of $$x$$ will be :
The time period of oscillation of a simple pendulum of length L suspended from the roof of a vehicle, which moves without friction down an inclined plane of inclination $$\alpha$$, is given by :
Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is -
(consider radius of earth $$R_{E}=6400 \mathrm{~km}$$ and $$\mathrm{g}$$ on earth $$10 \mathrm{~m} / \mathrm{s}^{2}$$ )
When a particle executes Simple Hormonic Motion, the nature of graph of velocity as a function of displacement will be :

In figure $$(\mathrm{A})$$, mass '$$2 \mathrm{~m}^{\text {' }}$$ is fixed on mass '$$\mathrm{m}$$ ' which is attached to two springs of spring constant $$\mathrm{k}$$. In figure (B), mass '$$\mathrm{m}$$' is attached to two springs of spring constant '$$\mathrm{k}$$' and '$$2 \mathrm{k}^{\prime}$$. If mass '$$\mathrm{m}$$' in (A) and in (B) are displaced by distance '$$x^{\prime}$$ horizontally and then released, then time period $$\mathrm{T}_{1}$$ and $$\mathrm{T}_{2}$$ corresponding to $$(\mathrm{A})$$ and (B) respectively follow the relation.
The motion of a simple pendulum executing S.H.M. is represented by the following equation.
$$y = A\sin (\pi t + \phi )$$, where time is measured in second. The length of pendulum is
Motion of a particle in x-y plane is described by a set of following equations $$x = 4\sin \left( {{\pi \over 2} - \omega t} \right)\,m$$ and $$y = 4\sin (\omega t)\,m$$. The path of the particle will be :
The equation of a particle executing simple harmonic motion is given by $$x = \sin \pi \left( {t + {1 \over 3}} \right)m$$. At t = 1s, the speed of particle will be
(Given : $$\pi$$ = 3.14)
The displacement of simple harmonic oscillator after 3 seconds starting from its mean position is equal to half of its amplitude. The time period of harmonic motion is :
Time period of a simple pendulum in a stationary lift is 'T'. If the lift accelerates with $${g \over 6}$$ vertically upwards then the time period will be :
(Where g = acceleration due to gravity)
Two massless springs with spring constants 2 k and 9 k, carry 50 g and 100 g masses at their free ends. These two masses oscillate vertically such that their maximum velocities are equal. Then, the ratio of their respective amplitudes will be :

(1) Potential energy is always equal to its K.E.
(2) Average potential and kinetic energy over any given time interval are always equal.
(3) Sum of the kinetic and potential energy at any point of time is constant.
(4) Average K.E. in one time period is equal to average potential energy in one time period.
Choose the most appropriate option from the options given below :

The potential energy U(x) versus time (t) plot of the particle is correctly shown in figure :
Statement I : A second's pendulum has a time period of 1 second.
Statement II : It takes precisely one second to move between the two extreme positions.
In the light of the above statements, choose the correct answer from the options given below :
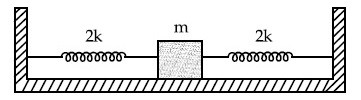


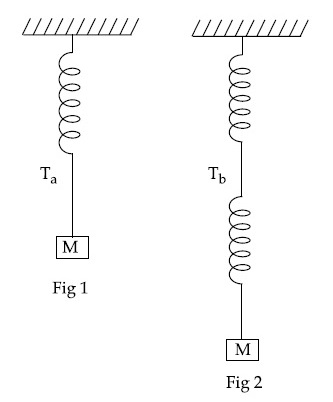
y(t) = y0 sin2 $$\omega $$t, where 'y' is measured from the lower end of unstretched spring. Then $$\omega $$ is:
(sketch is schematic and not to scale)
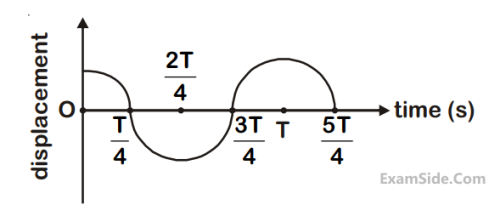
Which of the following statements is/are true for this motion?
(A) The force is zero at t = $${{3T} \over 4}$$
(B) The acceleration is maximum at t = T
(C) The speed is maximum at t = $${{T} \over 4}$$
(D) The P.E. is equal to K.E. of the oscillation at t = $${{T} \over 2}$$
x(t ) = e–0.1t cos (10$$\pi $$t + f).
Here t is in seconds. The time taken for its amplitude of vibration to drop to half of its initial value is close to :
y = 5 (sin 3 $$\pi $$ t + $$\sqrt 3 $$ cos 3 $$\pi $$t) cm
The amplitude and time period of the motion are :

V = $${1 \over 2}$$ k(x $$-$$ X)2. A particle of mass m comes from right with speed u and collides completely inelastically with M and sticks to it. This process repeats every time the oscillator crosses its equilibrium position. The amplitude of oscillations after 13 collisions is : (M = 10, m = 5, u = 1, k = 1)
x(t) = A sin (at + $$\delta $$)
y(t) = B sin (bt)
Identify the correct match below.
$$(graphs$$ $$are$$ $$schematic$$ $$and$$ $$not$$ $$drawn$$ $$to$$ $$scale)$$
($$g=$$ $$gravitational$$ $$acceleration$$)
$$x=4$$$$\left( {\cos \,\pi t + \sin \,\pi t} \right).$$ The amplitude of the particle is
Numerical
A particle of mass $$0.50 \mathrm{~kg}$$ executes simple harmonic motion under force $$F=-50(\mathrm{Nm}^{-1}) x$$. The time period of oscillation is $$\frac{x}{35} s$$. The value of $$x$$ is _________.
(Given $$\pi=\frac{22}{7}$$)
The position, velocity and acceleration of a particle executing simple harmonic motion are found to have magnitudes of $$4 \mathrm{~m}, 2 \mathrm{~ms}^{-1}$$ and $$16 \mathrm{~ms}^{-2}$$ at a certain instant. The amplitude of the motion is $$\sqrt{x}, \mathrm{~m}$$ where $$x$$ is _________.
An object of mass $$0.2 \mathrm{~kg}$$ executes simple harmonic motion along $$x$$ axis with frequency of $$\left(\frac{25}{\pi}\right) \mathrm{Hz}$$. At the position $$x=0.04 \mathrm{~m}$$ the object has kinetic energy $$0.5 \mathrm{~J}$$ and potential energy $$0.4 \mathrm{~J}$$. The amplitude of oscillation is ________ $$\mathrm{cm}$$.
A particle is doing simple harmonic motion of amplitude $$0.06 \mathrm{~m}$$ and time period $$3.14 \mathrm{~s}$$. The maximum velocity of the particle is _________ $$\mathrm{cm} / \mathrm{s}$$.
The displacement of a particle executing SHM is given by $$x=10 \sin \left(w t+\frac{\pi}{3}\right) m$$. The time period of motion is $$3.14 \mathrm{~s}$$. The velocity of the particle at $$t=0$$ is _______ $$\mathrm{m} / \mathrm{s}$$.
The time period of simple harmonic motion of mass $$M$$ in the given figure is $$\pi \sqrt{\frac{\alpha M}{5 k}}$$, where the value of $$\alpha$$ is _________.

A particle performs simple harmonic motion with amplitude $$A$$. Its speed is increased to three times at an instant when its displacement is $$\frac{2 A}{3}$$. The new amplitude of motion is $$\frac{n A}{3}$$. The value of $$n$$ is ___________.
A simple harmonic oscillator has an amplitude $$A$$ and time period $$6 \pi$$ second. Assuming the oscillation starts from its mean position, the time required by it to travel from $$x=$$ A to $$x=\frac{\sqrt{3}}{2}$$ A will be $$\frac{\pi}{x} \mathrm{~s}$$, where $$x=$$ _________.
When the displacement of a simple harmonic oscillator is one third of its amplitude, the ratio of total energy to the kinetic energy is $$\frac{x}{8}$$, where $$x=$$ _________.
A particle executes simple harmonic motion with an amplitude of $$4 \mathrm{~cm}$$. At the mean position, velocity of the particle is $$10 \mathrm{~cm} / \mathrm{s}$$. The distance of the particle from the mean position when its speed becomes $$5 \mathrm{~cm} / \mathrm{s}$$ is $$\sqrt{\alpha} \mathrm{~cm}$$, where $$\alpha=$$ ________.
At a given point of time the value of displacement of a simple harmonic oscillator is given as $$\mathrm{y}=\mathrm{A} \cos \left(30^{\circ}\right)$$. If amplitude is $$40 \mathrm{~cm}$$ and kinetic energy at that time is $$200 \mathrm{~J}$$, the value of force constant is $$1.0 \times 10^{x} ~\mathrm{Nm}^{-1}$$. The value of $$x$$ is ____________.
A rectangular block of mass $$5 \mathrm{~kg}$$ attached to a horizontal spiral spring executes simple harmonic motion of amplitude $$1 \mathrm{~m}$$ and time period $$3.14 \mathrm{~s}$$. The maximum force exerted by spring on block is _________ N
A simple pendulum with length $$100 \mathrm{~cm}$$ and bob of mass $$250 \mathrm{~g}$$ is executing S.H.M. of amplitude $$10 \mathrm{~cm}$$. The maximum tension in the string is found to be $$\frac{x}{40} \mathrm{~N}$$. The value of $$x$$ is ___________.
The amplitude of a particle executing SHM is $$3 \mathrm{~cm}$$. The displacement at which its kinetic energy will be $$25 \%$$ more than the potential energy is: __________ $$\mathrm{cm}$$
In the figure given below, a block of mass $$M=490 \mathrm{~g}$$ placed on a frictionless table is connected with two springs having same spring constant $$\left(\mathrm{K}=2 \mathrm{~N} \mathrm{~m}^{-1}\right)$$. If the block is horizontally displaced through '$$\mathrm{X}$$' $$\mathrm{m}$$ then the number of complete oscillations it will make in $$14 \pi$$ seconds will be _____________.

The general displacement of a simple harmonic oscillator is $$x = A\sin \omega t$$. Let T be its time period. The slope of its potential energy (U) - time (t) curve will be maximum when $$t = {T \over \beta }$$. The value of $$\beta$$ is ______________.
A particle of mass 250 g executes a simple harmonic motion under a periodic force $$\mathrm{F}=(-25~x)\mathrm{N}$$. The particle attains a maximum speed of 4 m/s during its oscillation. The amplitude of the motion is ___________ cm.
A mass m attached to free end of a spring executes SHM with a period of 1s. If the mass is increased by 3 kg the period of the oscillation increases by one second, the value of mass m is ___________ kg.

A block of a mass 2 kg is attached with two identical springs of spring constant 20 N/m each. The block is placed on a frictionless surface and the ends of the springs are attached to rigid supports (see figure). When the mass is displaced from its equilibrium position, it executes a simple harmonic motion. The time period of oscillation is $$\frac{\pi}{\sqrt x}$$ in SI unit. The value of $$x$$ is ____________.
The metallic bob of simple pendulum has the relative density 5. The time period of this pendulum is $$10 \mathrm{~s}$$. If the metallic bob is immersed in water, then the new time period becomes $$5 \sqrt{x}$$ s. The value of $$x$$ will be ________.
The potential energy of a particle of mass $$4 \mathrm{~kg}$$ in motion along the x-axis is given by $$\mathrm{U}=4(1-\cos 4 x)$$ J. The time period of the particle for small oscillation $$(\sin \theta \simeq \theta)$$ is $$\left(\frac{\pi}{K}\right) s$$. The value of $$\mathrm{K}$$ is _________.
A mass $$0.9 \mathrm{~kg}$$, attached to a horizontal spring, executes SHM with an amplitude $$\mathrm{A}_{1}$$. When this mass passes through its mean position, then a smaller mass of $$124 \mathrm{~g}$$ is placed over it and both masses move together with amplitude $$A_{2}$$. If the ratio $$\frac{A_{1}}{A_{2}}$$ is $$\frac{\alpha}{\alpha-1}$$, then the value of $$\alpha$$ will be ___________.
As per given figures, two springs of spring constants $$k$$ and $$2 k$$ are connected to mass $$m$$. If the period of oscillation in figure (a) is $$3 \mathrm{s}$$, then the period of oscillation in figure (b) will be $$\sqrt{x}~ s$$. The value of $$x$$ is ___________.

A body is performing simple harmonic with an amplitude of 10 cm. The velocity of the body was tripled by air jet when it is at 5 cm from its mean position. The new amplitude of vibration is $$\sqrt{x}$$ cm. The value of x is _____________.
A pendulum is suspended by a string of length 250 cm. The mass of the bob of the pendulum is 200 g. The bob is pulled aside until the string is at 60$$^\circ$$ with vertical as shown in the figure. After releasing the bob, the maximum velocity attained by the bob will be ____________ ms$$-$$1. (if g = 10 m/s2)

A particle executes simple harmonic motion. Its amplitude is 8 cm and time period is 6 s. The time it will take to travel from its position of maximum displacement to the point corresponding to half of its amplitude, is ___________ s.
$${x_1} = 5\sin \left( {2\pi t + {\pi \over 4}} \right)$$ and $${x_2} = 5\sqrt 2 (\sin 2\pi t + \cos 2\pi t)$$. The amplitude of second motion is ................ times the amplitude in first motion.
x(t) = A sin($$\omega$$t + $$\phi$$)
If the position and velocity of the particle at t = 0 s are 2 cm and 2$$\omega$$ cm s$$-$$1 respectively, then its amplitude is $$x\sqrt 2 $$ cm where the value of x is _________________.