Properties of Matter · Physics · JEE Main
MCQ (Single Correct Answer)
A 3 m long wire of radius 3 mm shows an extension of 0.1 mm when loaded vertically by a mass of 50 kg in an experiment to determine Young's modulus. The value of Young's modulus of the wire as per this experiment is $P \times 10^{11} \, \text{Nm}^{-2}$, where the value of $P$ is: (Take $g = 3\pi \, \text{m/s}^2$)
A capillary tube of radius 0.1 mm is partly dipped in water (surface tension 70 dyn/cm and glass water contact angle ≈ 0°) with 30° inclined with the vertical. The length of water risen in the capillary is _______ cm. (Take $g = 9.8 \text{ m/s}^2$)
Two wires A and B are made of same material having ratio of lengths $\frac{L_A}{L_B}=\frac{1}{3}$ and their diameters ratio $\frac{d_A}{d_B}=2$. If both the wires are stretched using same force, what would be the ratio of their respective elongations?
A cylindrical rod of length 1 m and radius 4 cm is mounted vertically. It is subjected to a shear force of $10^5 \mathrm{~N}$ at the top. Considering infinitesimally small displacement in the upper edge, the angular displacement $\theta$ of the rod axis from its original position would be : (shear moduli, $G=10^{10} \mathrm{~N} / \mathrm{m}^2$ )
Two liquids $A$ and $B$ have $\theta_A$ and $\theta_B$ as contact angles in a capillary tube. If $K=\cos \theta_A / \cos \theta_B$, then identify the correct statement:
A solid steel ball of diameter 3.6 mm acquired terminal velocity $2.45 \times 10^{-2} \mathrm{~m} / \mathrm{s}$ while falling under gravity through an oil of density $925 \mathrm{~kg} \mathrm{~m}^{-3}$. Take density of steel as $7825 \mathrm{~kg} \mathrm{~m}^{-3}$ and g as $9.8 \mathrm{~m} / \mathrm{s}^2$. The viscosity of the oil in SI unit is
Consider a completely full cylindrical water tank of height 1.6 m and of cross-sectional area $0.5 \mathrm{~m}^2$. It has a small hole in its side at a height 90 cm from the bottom. Assume, the crosssectional area of the hole to be negligibly small as compared to that of the water tank. If a load 50 kg is applied at the top surface of the water in the tank then the velocity of the water coming out at the instant when the hole is opened is:
$$ \left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2\right) $$
The fractional compression $\left( \frac{\Delta V}{V} \right)$ of water at the depth of 2.5 km below the sea level is __________ %. Given, the Bulk modulus of water = $2 \times 10^9$ N m$^{-2}$, density of water = $10^3$ kg m$^{-3}$, acceleration due to gravity $g = 10$ m s$^{-2}$.
A 400 g solid cube having an edge of length 10 cm floats in water. How much volume of the cube is outside the water?
(Given: density of water = 1000 kg m-3)
In the experiment for measurement of viscosity ' $\eta$ ' of given liquid with a ball having radius $R$, consider following statements.
A. Graph between terminal velocity V and R will be a parabola.
B. The terminal velocities of different diameter balls are constant for a given liquid.
C. Measurement of terminal velocity is dependent on the temperature.
D. This experiment can be utilized to assess the density of a given liquid.
E. If balls are dropped with some initial speed, the value of $\eta$ will change.
Choose the correct answer from the options given below:
Consider following statements:
A. Surface tension arises due to extra energy of the molecules at the interior as compared to the molecules at the surface, of a liquid.
B. As the temperature of liquid rises, the coefficient of viscosity increases.
C. As the temperature of gas increases, the coefficient of viscosity increases
D. The onset of turbulence is determined by Reynold's number.
E. In a steady flow two stream lines never intersect.
Choose the correct answer from the options given below:
The amount of work done to break a big water drop of radius ' $R$ ' into 27 small drops of equal radius is 10 J . The work done required to break the same big drop into 64 small drops of equal radius will be
A massless spring gets elongated by amount $x_1$ under a tension of 5 N . Its elongation is $x_2$ under the tension of 7 N . For the elongation of $\left(5 x_1-2 x_2\right)$, the tension in the spring will be,
Water flows in a horizontal pipe whose one end is closed with a valve. The reading of the pressure gauge attached to the pipe is $P_1$. The reading of the pressure gauge falls to $P_2$ when the valve is opened. The speed of water flowing in the pipe is proportional to
Given below are two statements:
Statement I: The hot water flows faster than cold water
Statement II: Soap water has higher surface tension as compared to fresh water. In the light above statements, choose the correct answer from the options given below

A tube of length $L$ is shown in the figure. The radius of cross section at the point $(1)$ is 2 cm and at the point (2) is 1 cm , respectively. If the velocity of water entering at point (1) is $2 \mathrm{~m} / \mathrm{s}$, then velocity of water leaving the point (2) will be
A small rigid spherical ball of mass M is dropped in a long vertical tube containing glycerine. The velocity of the ball becomes constant after some time. If the density of glycerine is half of the density of the ball, then the viscous force acting on the ball will be (consider g as acceleration due to gravity)
The excess pressure inside a soap bubble is thrice the excess pressure inside a second soap bubble. The ratio between the volume of the first and the second bubble is:
A spherical ball of radius $$1 \times 10^{-4} \mathrm{~m}$$ and density $$10^5 \mathrm{~kg} / \mathrm{m}^3$$ falls freely under gravity through a distance $$h$$ before entering a tank of water, If after entering in water the velocity of the ball does not change, then the value of $$h$$ is approximately:
(The coefficient of viscosity of water is $$9.8 \times 10^{-6} \mathrm{~N} \mathrm{~s} / \mathrm{m}^2$$)
A sphere of relative density $$\sigma$$ and diameter $$D$$ has concentric cavity of diameter $$d$$. The ratio of $$\frac{D}{d}$$, if it just floats on water in a tank is :
A cube of ice floats partly in water and partly in kerosene oil. The ratio of volume of ice immersed in water to that in kerosene oil (specific gravity of Kerosene oil = 0.8, specific gravity of ice = 0.9):

Young's modulus is determined by the equation given by $$\mathrm{Y}=49000 \frac{\mathrm{m}}{\mathrm{l}} \frac{\mathrm{dyne}}{\mathrm{cm}^2}$$ where $$M$$ is the mass and $$l$$ is the extension of wire used in the experiment. Now error in Young modules $$(Y)$$ is estimated by taking data from $$M-l$$ plot in graph paper. The smallest scale divisions are $$5 \mathrm{~g}$$ and $$0.02 \mathrm{~cm}$$ along load axis and extension axis respectively. If the value of $M$ and $l$ are $$500 \mathrm{~g}$$ and $$2 \mathrm{~cm}$$ respectively then percentage error of $$Y$$ is :
Correct Bernoulli's equation is (symbols have their usual meaning) :
Pressure inside a soap bubble is greater than the pressure outside by an amount : (given : $$\mathrm{R}=$$ Radius of bubble, $$\mathrm{S}=$$ Surface tension of bubble)
A small ball of mass $$m$$ and density $$\rho$$ is dropped in a viscous liquid of density $$\rho_0$$. After sometime, the ball falls with constant velocity. The viscous force on the ball is :
Match List I with List II :
| LIST I |
LIST II |
||
|---|---|---|---|
| A. | A force that restores an elastic body of unit area to its original state | I. | Bulk modulus |
| B. | Two equal and opposite forces parallel to opposite faces | II. | Young's modulus |
| C. | Forces perpendicular everywhere to the surface per unit area same everywhere | III. | Stress |
| D. | Two equal and opposite forces perpendicular to opposite faces Choose the correct answer from the options given below : | IV. | Shear modulus |
Choose the correct answer from the options given below :
Given below are two statements :
Statement I : When a capillary tube is dipped into a liquid, the liquid neither rises nor falls in the capillary. The contact angle may be $$0^{\circ}$$.
Statement II : The contact angle between a solid and a liquid is a property of the material of the solid and liquid as well.
In the light of the above statement, choose the correct answer from the options given below.
Given below are two statements :
Statement I : The contact angle between a solid and a liquid is a property of the material of the solid and liquid as well.
Statement II : The rise of a liquid in a capillary tube does not depend on the inner radius of the tube.
In the light of the above statements, choose the correct answer from the options given below :
Given below are two statements :
Statement I : When speed of liquid is zero everywhere, pressure difference at any two points depends on equation $$\mathrm{P}_1-\mathrm{P}_2=\rho g\left(\mathrm{~h}_2-\mathrm{h}_1\right)$$.
Statement II : In ventury tube shown $$2 \mathrm{gh}=v_1^2-v_2^2$$

In the light of the above statements, choose the most appropriate answer from the options given below.
A small spherical ball of radius $$r$$, falling through a viscous medium of negligible density has terminal velocity '$$v$$'. Another ball of the same mass but of radius $$2 r$$, falling through the same viscous medium will have terminal velocity:
A small steel ball is dropped into a long cylinder containing glycerine. Which one of the following is the correct representation of the velocity time graph for the transit of the ball?
Young's modules of material of a wire of length '$$L$$' and cross-sectional area $$A$$ is $$Y$$. If the length of the wire is doubled and cross-sectional area is halved then Young's modules will be :
A small liquid drop of radius $$R$$ is divided into 27 identical liquid drops. If the surface tension is $$T$$, then the work done in the process will be:
A wire of length $$L$$ and radius $$r$$ is clamped at one end. If its other end is pulled by a force $$F$$, its length increases by $$l$$. If the radius of the wire and the applied force both are reduced to half of their original values keeping original length constant, the increase in length will become:
Given below are two statements:
Statement I : If a capillary tube is immersed first in cold water and then in hot water, the height of capillary rise will be smaller in hot water.
Statement II : If a capillary tube is immersed first in cold water and then in hot water, the height of capillary rise will be smaller in cold water.
In the light of the above statements, choose the most appropriate from the options given below
Given below are two statements : one is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : The property of body, by virtue of which it tends to regain its original shape when the external force is removed, is Elasticity.
Reason (R) : The restoring force depends upon the bonded inter atomic and inter molecular force of solid.
In the light of the above statements, choose the correct answer from the options given below :
Given below are two statements :
Statement (I) :Viscosity of gases is greater than that of liquids.
Statement (II) : Surface tension of a liquid decreases due to the presence of insoluble impurities.
In the light of the above statements, choose the most appropriate answer from the options given below :
Given below are two statements: one is labelled as Assertion $$\mathbf{A}$$ and the other is labelled as Reason $$\mathbf{R}$$
Assertion A : A spherical body of radius $$(5 \pm 0.1) \mathrm{mm}$$ having a particular density is falling through a liquid of constant density. The percentage error in the calculation of its terminal velocity is $$4 \%$$.
Reason R : The terminal velocity of the spherical body falling through the liquid is inversely proportional to its radius.
In the light of the above statements, choose the correct answer from the options given below

The figure shows a liquid of given density flowing steadily in horizontal tube of varying cross - section. Cross sectional areas at $$\mathrm{A}$$ is $$1.5 \mathrm{~cm}^{2}$$, and $$\mathrm{B}$$ is $$25 \mathrm{~mm}^{2}$$, if the speed of liquid at $$\mathrm{B}$$ is $$60 \mathrm{~cm} / \mathrm{s}$$ then $$\left(\mathrm{P}_{\mathrm{A}}-\mathrm{P}_{\mathrm{B}}\right)$$ is :
(Given $$\mathrm{P}_{\mathrm{A}}$$ and $$\mathrm{P}_{\mathrm{B}}$$ are liquid pressures at $$\mathrm{A}$$ and $$\mathrm{B}$$% points.
density $$\rho=1000 \mathrm{~kg} \mathrm{~m}^{-3}$$
$$\mathrm{A}$$ and $$\mathrm{B}$$ are on the axis of tube
Under isothermal condition, the pressure of a gas is given by $$\mathrm{P}=a \mathrm{~V}^{-3}$$, where $$a$$ is a constant and $$\mathrm{V}$$ is the volume of the gas. The bulk modulus at constant temperature is equal to
A body cools from $$80^{\circ} \mathrm{C}$$ to $$60^{\circ} \mathrm{C}$$ in 5 minutes. The temperature of the surrounding is $$20^{\circ} \mathrm{C}$$. The time it takes to cool from $$60^{\circ} \mathrm{C}$$ to $$40^{\circ} \mathrm{C}$$ is :
Eight equal drops of water are falling through air with a steady speed of $$10 \mathrm{~cm} / \mathrm{s}$$. If the drops coalesce, the new velocity is:-
Young's moduli of the material of wires A and B are in the ratio of $$1: 4$$, while its area of cross sections are in the ratio of $$1: 3$$. If the same amount of load is applied to both the wires, the amount of elongation produced in the wires $$\mathrm{A}$$ and $$\mathrm{B}$$ will be in the ratio of
[Assume length of wires A and B are same]
Given below are two statements:
Statement I : Pressure in a reservoir of water is same at all points at the same level of water.
Statement II : The pressure applied to enclosed water is transmitted in all directions equally.
In the light of the above statements, choose the correct answer from the options given below:
A hydraulic automobile lift is designed to lift vehicles of mass $$5000 \mathrm{~kg}$$. The area of cross section of the cylinder carrying the load is $$250 \mathrm{~cm}^{2}$$. The maximum pressure the smaller piston would have to bear is $$\left[\right.$$ Assume $$\left.g=10 \mathrm{~m} / \mathrm{s}^{2}\right]$$
An air bubble of volume $$1 \mathrm{~cm}^{3}$$ rises from the bottom of a lake $$40 \mathrm{~m}$$ deep to the surface at a temperature of $$12^{\circ} \mathrm{C}$$. The atmospheric pressure is $$1 \times 10^{5} \mathrm{~Pa}$$ the density of water is $$1000 \mathrm{~kg} / \mathrm{m}^{3}$$ and $$\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}$$. There is no difference of the temperature of water at the depth of $$40 \mathrm{~m}$$ and on the surface. The volume of air bubble when it reaches the surface will be:
An aluminium rod with Young's modulus $$Y=7.0 \times 10^{10} \mathrm{~N} / \mathrm{m}^{2}$$ undergoes elastic strain of $$0.04 \%$$. The energy per unit volume stored in the rod in SI unit is:
Given below are two statements: one is labelled as Assertion $$\mathbf{A}$$ and the other is labelled as Reason $$\mathbf{R}$$
Assertion A: When you squeeze one end of a tube to get toothpaste out from the other end, Pascal's principle is observed.
Reason R: A change in the pressure applied to an enclosed incompressible fluid is transmitted undiminished to every portion of the fluid and to the walls of its container.
In the light of the above statements, choose the most appropriate answer from the options given below
A small ball of mass $$\mathrm{M}$$ and density $$\rho$$ is dropped in a viscous liquid of density $$\rho_{0}$$. After some time, the ball falls with a constant velocity. What is the viscous force on the ball ?
The Young's modulus of a steel wire of length $$6 \mathrm{~m}$$ and cross-sectional area $$3 \mathrm{~mm}^{2}$$, is $$2 \times 10^{11}~\mathrm{N} / \mathrm{m}^{2}$$. The wire is suspended from its support on a given planet. A block of mass $$4 \mathrm{~kg}$$ is attached to the free end of the wire. The acceleration due to gravity on the planet is $$\frac{1}{4}$$ of its value on the earth. The elongation of wire is (Take $$g$$ on the earth $$=10 \mathrm{~m} / \mathrm{s}^{2}$$) :
A mercury drop of radius $$10^{-3}~\mathrm{m}$$ is broken into 125 equal size droplets. Surface tension of mercury is $$0.45~\mathrm{Nm}^{-1}$$. The gain in surface energy is :
If 1000 droplets of water of surface tension $$0.07 \mathrm{~N} / \mathrm{m}$$, having same radius $$1 \mathrm{~mm}$$ each, combine to from a single drop. In the process the released surface energy is :-
$$\left( {\mathrm{Take}\,\pi = {{22} \over 7}} \right)$$
The height of liquid column raised in a capillary tube of certain radius when dipped in liquid A vertically is, $$5 \mathrm{~cm}$$. If the tube is dipped in a similar manner in another liquid $$\mathrm{B}$$ of surface tension and density double the values of liquid $$\mathrm{A}$$, the height of liquid column raised in liquid $$\mathrm{B}$$ would be __________ m.
Choose the correct relationship between Poisson ratio $$(\sigma)$$, bulk modulus (K) and modulus of rigidity $$(\eta)$$ of a given solid object :
A fully loaded boeing aircraft has a mass of $$5.4\times10^5$$ kg. Its total wing area is 500 m$$^2$$. It is in level flight with a speed of 1080 km/h. If the density of air $$\rho$$ is 1.2 kg m$$^{-3}$$, the fractional increase in the speed of the air on the upper surface of the wing relative to the lower surface in percentage will be. ($$\mathrm{g=10~m/s^2}$$)
Surface tension of a soap bubble is $$2.0 \times 10^{-2} \mathrm{Nm}^{-1}$$. Work done to increase the radius of soap bubble from $$3.5 \mathrm{~cm}$$ to $$7 \mathrm{~cm}$$ will be:
Take $$\left[\pi=\frac{22}{7}\right]$$
A bicycle tyre is filled with air having pressure of $$270 ~\mathrm{kPa}$$ at $$27^{\circ} \mathrm{C}$$. The approximate pressure of the air in the tyre when the temperature increases to $$36^{\circ} \mathrm{C}$$ is
Match List I with List II
| List I | List II | ||
|---|---|---|---|
| A. | Surface tension | I. | $$\mathrm{kg~m^{-1}~s^{-1}}$$ |
| B. | Pressure | II. | $$\mathrm{kg~ms^{-1}}$$ |
| C. | Viscosity | III. | $$\mathrm{kg~m^{-1}~s^{-2}}$$ |
| D. | Impulse | IV. | $$\mathrm{kg~s^{-2}}$$ |
Choose the correct answer from the options given below :
A bowl filled with very hot soup cools from 98$$^\circ$$C to 86$$^\circ$$C in 2 minutes when the room temperature is 22$$^\circ$$C. How long it will take to cool from 75$$^\circ$$C to 69$$^\circ$$C?
Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R
Assertion A : Steel is used in the construction of buildings and bridges.
Reason R : Steel is more elastic and its elastic limit is high.
In the light of above statements, choose the most appropriate answer from the options given below
The frequency ($$\nu$$) of an oscillating liquid drop may depend upon radius ($$r$$) of the drop, density ($$\rho$$) of liquid and the surface tension (s) of the liquid as $$\nu=r^a\rho^b s^c$$. The values of a, b and c respectively are
A 100 m long wire having cross-sectional area $$\mathrm{6.25\times10^{-4}~m^2}$$ and Young's modulus is $$\mathrm{10^{10}~Nm^{-2}}$$ is subjected to a load of 250 N, then the elongation in the wire will be :
Given below are two statements : One is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A): Clothes containing oil or grease stains cannot be cleaned by water wash.
Reason (R): Because the angle of contact between the oil/grease and water is obtuse.
In the light of the above statements, choose the correct answer from the option given below.
If the length of a wire is made double and radius is halved of its respective values. Then, the Young's modulus of the material of the wire will :
A pressure-pump has a horizontal tube of cross sectional area $$10 \mathrm{~cm}^{2}$$ for the outflow of water at a speed of $$20 \mathrm{~m} / \mathrm{s}$$. The force exerted on the vertical wall just in front of the tube which stops water horizontally flowing out of the tube, is :
[given: density of water $$=1000 \mathrm{~kg} / \mathrm{m}^{3}$$]
Consider a cylindrical tank of radius $$1 \mathrm{~m}$$ is filled with water. The top surface of water is at $$15 \mathrm{~m}$$ from the bottom of the cylinder. There is a hole on the wall of cylinder at a height of $$5 \mathrm{~m}$$ from the bottom. A force of $$5 \times 10^{5} \mathrm{~N}$$ is applied an the top surface of water using a piston. The speed of ifflux from the hole will be : (given atmospheric pressure $$\mathrm{P}_{\mathrm{A}}=1.01 \times 10^{5} \mathrm{~Pa}$$, density of water $$\rho_{\mathrm{W}}=1000 \mathrm{~kg} / \mathrm{m}^{3}$$ and gravitational acceleration $$\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}$$ )

A balloon has mass of $$10 \mathrm{~g}$$ in air. The air escapes from the balloon at a uniform rate with velocity $$4.5 \mathrm{~cm} / \mathrm{s}$$. If the balloon shrinks in $$5 \mathrm{~s}$$ completely. Then, the average force acting on that balloon will be (in dyne).
The force required to stretch a wire of cross-section $$1 \mathrm{~cm}^{2}$$ to double its length will be : (Given Yong's modulus of the wire $$=2 \times 10^{11} \mathrm{~N} / \mathrm{m}^{2}$$)
A steel wire of length $$3.2 \mathrm{~m}\left(\mathrm{Y}_{\mathrm{s}}=2.0 \times 10^{11} \,\mathrm{Nm}^{-2}\right)$$ and a copper wire of length $$4.4 \mathrm{~m}\left(\mathrm{Y}_{\mathrm{c}}=1.1 \times 10^{11} \,\mathrm{Nm}^{-2}\right)$$, both of radius $$1.4 \mathrm{~mm}$$ are connected end to end. When stretched by a load, the net elongation is found to be $$1.4 \mathrm{~mm}$$. The load applied, in Newton, will be: $$\quad\left(\right.$$ Given $$\pi=\frac{22}{7}$$)
Two cylindrical vessels of equal cross-sectional area $$16 \mathrm{~cm}^{2}$$ contain water upto heights $$100 \mathrm{~cm}$$ and $$150 \mathrm{~cm}$$ respectively. The vessels are interconnected so that the water levels in them become equal. The work done by the force of gravity during the process, is [Take, density of water $$=10^{3} \mathrm{~kg} / \mathrm{m}^{3}$$ and $$\mathrm{g}=10 \mathrm{~ms}^{-2}$$ ] :
The area of cross section of the rope used to lift a load by a crane is $$2.5 \times 10^{-4} \mathrm{~m}^{2}$$. The maximum lifting capacity of the crane is 10 metric tons. To increase the lifting capacity of the crane to 25 metric tons, the required area of cross section of the rope should be :
(take $$g=10 \,m s^{-2}$$ )
A water drop of radius $$1 \mathrm{~cm}$$ is broken into 729 equal droplets. If surface tension of water is 75 dyne/ $$\mathrm{cm}$$, then the gain in surface energy upto first decimal place will be :
(Given $$\pi=3.14$$ )
A drop of liquid of density $$\rho$$ is floating half immersed in a liquid of density $${\sigma}$$ and surface tension $$7.5 \times 10^{-4}$$ Ncm$$-$$1. The radius of drop in $$\mathrm{cm}$$ will be :
(g = 10 ms$$-$$2)
An air bubble of negligible weight having radius r rises steadily through a solution of density $$\sigma$$ at speed v. The coefficient of viscosity of the solution is given by :
A wire of length L is hanging from a fixed support. The length changes to L1 and L2 when masses 1 kg and 2 kg are suspended respectively from its free end. Then the value of L is equal to :
A block of metal weighing 2 kg is resting on a frictionless plane (as shown in figure). It is struck by a jet releasing water at a rate of 1 kgs$$-$$1 and at a speed of 10 ms$$-$$1. Then, the initial acceleration of the block, in ms$$-$$2, will be :

A water drop of radius 1 $$\mu$$m falls in a situation where the effect of buoyant force is negligible. Co-efficient of viscosity of air is 1.8 $$\times$$ 10$$-$$5 Nsm$$-$$2 and its density is negligible as compared to that of water 106 gm$$-$$3. Terminal velocity of the water drop is :
(Take acceleration due to gravity = 10 ms$$-$$2)
Given below are two statements : One is labelled as Assertion A and the other is labelled as Reason R.
Assertion A : Product of Pressure (P) and time (t) has the same dimension as that of coefficient of viscosity.
Reason R : Coefficient of viscosity = $${{Force} \over {Velocity\,gradient}}$$
Choose the correct answer from the options given below :
A water drop of diameter 2 cm is broken into 64 equal droplets. The surface tension of water is 0.075 N/m. In this process the gain in surface energy will be :
When a ball is dropped into a lake from a height 4.9 m above the water level, it hits the water with a velocity v and then sinks to the bottom with the constant velocity v. It reaches the bottom of the lake 4.0 s after it is dropped. The approximate depth of the lake is :
The velocity of a small ball of mass 'm' and density d1, when dropped in a container filled with glycerin, becomes constant after some time. If the density of glycerin is d2, then the viscous force acting on the ball, will be :
If p is the density and $$\eta$$ is coefficient of viscosity of fluid which flows with a speed v in the pipe of diameter d, the correct formula for Reynolds number Re is :
The terminal velocity (vt) of the spherical rain drop depends on the radius (r) of the spherical rain drop as :
Potential energy as a function of r is given by $$U = {A \over {{r^{10}}}} - {B \over {{r^5}}}$$, where r is the interatomic distance, A and B are positive constants. The equilibrium distance between the two atoms will be :
The bulk modulus of a liquid is 3 $$\times$$ 1010 Nm$$-$$2. The pressure required to reduce the volume of liquid by 2% is :
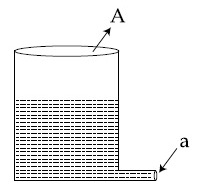
[Density of water fw = 1000 kg m$$-$$3 and Density of air fa = 1.2 kg m$$-$$3, g = 10 m/s2, Coefficient of viscosity of air = 1.8 $$\times$$ 10$$-$$5 Nsm$$-$$2]
(Assume that atmospheric pressure is 1 $$\times$$ 105 Pa density of water is 103 kg m$$-$$3, g = 10 ms$$-$$2)
speed v ms–1 at a point where the pressure is P pascal. At another point where pressure is $${P \over 2}$$ Pascal its speed is V ms–1. If the density of the fluid is $$\rho $$ kg m–3 and the flow is streamline, then V is equal to :
(ignore viscosity of air)
(Given bulk modulus of metal, B = 8 $$ \times $$ 1010 Pa)
The pressure of water changes by 700 Nm–2
between A and B where the area of cross section
are 40 cm2 and 20 cm2, respectively. Find the
rate of flow of water through the tube.
(density of water = 1000 kgm–3)

$$\rho \left( r \right) = {\rho _0}\left( {1 - {{{r^2}} \over {{R^2}}}} \right)$$ , $$0 < r \le R$$
The minimum density of a liquid in which it will float is :
The new value of increase in length of the steel wire is:

If P2 is 4P1 and l2 is $${{{1_1}} \over 4}$$, then the radius r2 will be equal to :


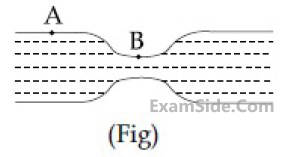
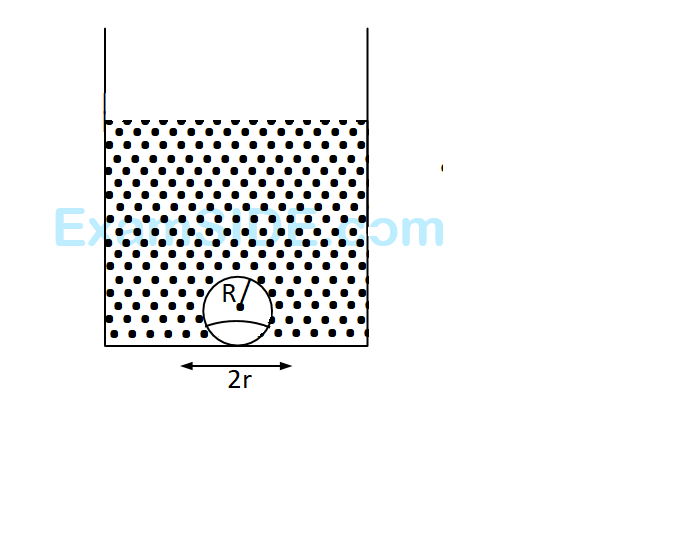
Consider a water jar of radius R that has water filled up to height H and is kept on astand of height h (see figure). Through a hole of radius r (r << R) at its bottom, the water leaks out and the stream of water coming down towards the ground has a shape like a funnel as shown in the figure. If the radius of the cross-section of water stream when it hits the ground is x. Then :
Numerical
A sample of a liquid is kept at 1 atm. It is compressed to 5 atm which leads to a change of volume of 0.8 cm3. If the bulk modulus of the liquid is 2 GPa, the initial volume of the liquid was _______ litre.
(Take 1 atm = 105 Pa)
A cube having a side of 10 cm with unknown mass and 200 gm mass were hung at two ends of a uniform rigid rod of 27 cm long. The rod along with masses was placed on a wedge keeping the distance between wedge point and 200 gm weight as 25 cm. Initially the masses were not at balance. A beaker is placed beneath the unknown mass and water is added slowly to it. At given point the masses were in balance and half volume of the unknown mass was inside the water.
(Take the density of unknown mass is more than that of the water, the mass did not absorb water and water density is 1 gm/cm3.)
The unknown mass is _____ kg.
Two slabs with square cross section of different materials $(1,2)$ with equal sides $(l)$ and thickness $d_1$ and $d_2$ such that $d_2=2 d_1$ and $l>d_2$. Considering lower edges of these slabs are fixed to the floor, we apply equal shearing force on the narrow faces. The angle of deformation is $\theta_2=2 \theta_1$. If the shear moduli of material 1 is $4 \times 10^9 \mathrm{~N} / \mathrm{m}^2$, then shear moduli of material 2 is $x \times 10^9 \mathrm{~N} / \mathrm{m}^2$, where value of $x$ is ________.
The excess pressure inside a soap bubble A in air is half the excess pressure inside another soap bubble B in air. If the volume of the bubble A is $n$ times the volume of the bubble $B$, then, the value of $n$ is__________.
A steel wire of length 2 m and Young's modulus $2.0 \times 10^{11} \mathrm{~N} \mathrm{~m}^{-2}$ is stretched by a force. If Poisson ratio and transverse strain for the wire are 0.2 and $10^{-3}$ respectively, then the elastic potential energy density of the wire is __________ $\times 10^5$ (in SI units).
A vessel with square cross-section and height of 6 m is vertically partitioned. A small window of $100 \mathrm{~cm}^2$ with hinged door is fitted at a depth of 3 m in the partition wall. One part of the vessel is filled completely with water and the other side is filled with the liquid having density $1.5 \times 10^3 \mathrm{~kg} / \mathrm{m}^3$. What force one needs to apply on the hinged door so that it does not get opened ?
$$\text { (Acceleration due to gravity }=10 \mathrm{~m} / \mathrm{s}^2 \text { ) }$$
The volume contraction of a solid copper cube of edge length 10 cm , when subjected to a hydraulic pressure of $7 \times 10^{6} ~\mathrm{Pa}$, would be __________ $\mathrm{mm}{ }^3$.
(Given bulk modulus of copper $=1.4 \times 10^{11} \mathrm{~N} \mathrm{~m}^{-2}$ )
In a measurement, it is asked to find modulus of elasticity per unit torque applied on the system. The measured quantity has dimension of $\left[M^a L^b T^c\right]$. If $b=3$, the value of $c$ is _________.
The increase in pressure required to decrease the volume of a water sample by $0.2 \%$ is $\mathrm{P} \times 10^5 \mathrm{Nm}^{-2}$. Bulk modulus of water is $2.15 \times 10^9 \mathrm{Nm}^{-2}$. The value of P is _________ .
An air bubble of radius 1.0 mm is observed at a depth 20 cm below the free surface of a liquid having surface tension $0.095 \mathrm{~J} / \mathrm{m}^2$ and density $10^3 \mathrm{~kg} / \mathrm{m}^3$. The difference between pressure inside the bubble and atmospheric pressure is __________ $\mathrm{N} / \mathrm{m}^2$. (Take $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ )
Two soap bubbles of radius 2 cm and 4 cm , respectively, are in contact with each other. The radius of curvature of the common surface, in cm , is _________.
Two persons pull a wire towards themselves. Each person exerts a force of $$200 \mathrm{~N}$$ on the wire. Young's modulus of the material of wire is $$1 \times 10^{11} \mathrm{~N} \mathrm{~m}^{-2}$$. Original length of the wire is $$2 \mathrm{~m}$$ and the area of cross section is $$2 \mathrm{~cm}^2$$. The wire will extend in length by _________ $$\mu \mathrm{m}$$.
Small water droplets of radius $$0.01 \mathrm{~mm}$$ are formed in the upper atmosphere and falling with a terminal velocity of $$10 \mathrm{~cm} / \mathrm{s}$$. Due to condensation, if 8 such droplets are coalesced and formed a larger drop, the new terminal velocity will be ________ $$\mathrm{cm} / \mathrm{s}$$.
A liquid column of height $$0.04 \mathrm{~cm}$$ balances excess pressure of a soap bubble of certain radius. If density of liquid is $$8 \times 10^3 \mathrm{~kg} \mathrm{~m}^{-3}$$ and surface tension of soap solution is $$0.28 \mathrm{~Nm}^{-1}$$, then diameter of the soap bubble is __________ $$\mathrm{cm}$$. (if $$\mathrm{g}=10 \mathrm{~m} \mathrm{~s}^{-2}$$ )
A wire of cross sectional area A, modulus of elasticity $$2 \times 10^{11} \mathrm{~Nm}^{-2}$$ and length $$2 \mathrm{~m}$$ is stretched between two vertical rigid supports. When a mass of $$2 \mathrm{~kg}$$ is suspended at the middle it sags lower from its original position making angle $$\theta=\frac{1}{100}$$ radian on the points of support. The value of A is ________ $$\times 10^{-4} \mathrm{~m}^2$$ (consider $$x<<\mathrm{L}$$ ).
(given : $$\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$$)

A big drop is formed by coalescing 1000 small droplets of water. The ratio of surface energy of 1000 droplets to that of energy of big drop is $$\frac{10}{x}$$. The value of $$x$$ is ________.

A hydraulic press containing water has two arms with diameters as mentioned in the figure. A force of $$10 \mathrm{~N}$$ is applied on the surface of water in the thinner arm. The force required to be applied on the surface of water in the thicker arm to maintain equilibrium of water is _________ N.
The density and breaking stress of a wire are $$6 \times 10^4 \mathrm{~kg} / \mathrm{m}^3$$ and $$1.2 \times 10^8 \mathrm{~N} / \mathrm{m}^2$$ respectively. The wire is suspended from a rigid support on a planet where acceleration due to gravity is $$\frac{1}{3}^{\text {rd }}$$ of the value on the surface of earth. The maximum length of the wire with breaking is _______ $$\mathrm{m}$$ (take, $$\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$$).
Mercury is filled in a tube of radius $$2 \mathrm{~cm}$$ up to a height of $$30 \mathrm{~cm}$$. The force exerted by mercury on the bottom of the tube is _________ N.
(Given, atmospheric pressure $$=10^5 \mathrm{~Nm}^{-2}$$, density of mercury $$=1.36 \times 10^4 \mathrm{~kg} \mathrm{~m}^{-3}, \mathrm{~g}=10 \mathrm{~m} \mathrm{~s}^{-2}, \pi=\frac{22}{7})$$
A soap bubble is blown to a diameter of $$7 \mathrm{~cm}$$. $$36960 \mathrm{~erg}$$ of work is done in blowing it further. If surface tension of soap solution is 40 dyne/$$\mathrm{cm}$$ then the new radius is ________ cm Take $$(\pi=\frac{22}{7})$$.
An elastic spring under tension of $$3 \mathrm{~N}$$ has a length $$a$$. Its length is $$b$$ under tension $$2 \mathrm{~N}$$. For its length $$(3 a-2 b)$$, the value of tension will be _______ N.
[Area of cross section of wire $=0.005 \mathrm{~cm}^2, \mathrm{Y}=2 \times 10^{11} \mathrm{Nm}^{-2}$ and $\mathrm{g}=10 \mathrm{~ms}^{-2}$ ]
(Take air density to be $1 \mathrm{~kg} \mathrm{~m}^{-3}$ and $\mathrm{g}=10 \mathrm{~ms}^{-2}$ )
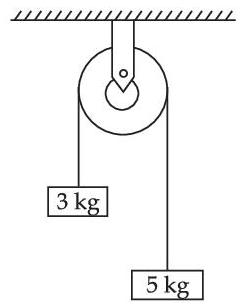
Two blocks of mass $$2 \mathrm{~kg}$$ and $$4 \mathrm{~kg}$$ are connected by a metal wire going over a smooth pulley as shown in figure. The radius of wire is $$4.0 \times 10^{-5} \mathrm{~m}$$ and Young's modulus of the metal is $$2.0 \times 10^{11} \mathrm{~N} / \mathrm{m}^2$$. The longitudinal strain developed in the wire is $$\frac{1}{\alpha \pi}$$. The value of $$\alpha$$ is _________. [Use $$g=10 \mathrm{~m} / \mathrm{s}^2$$]

The depth below the surface of sea to which a rubber ball be taken so as to decrease its volume by $$0.02 \%$$ is _______ $$m$$.
(Take density of sea water $$=10^3 \mathrm{kgm}^{-3}$$, Bulk modulus of rubber $$=9 \times 10^8 \mathrm{~Nm}^{-2}$$, and $$g=10 \mathrm{~ms}^{-2}$$)
A big drop is formed by coalescing 1000 small identical drops of water. If $$E_1$$ be the total surface energy of 1000 small drops of water and $$E_2$$ be the surface energy of single big drop of water, then $$E_1: E_2$$ is $$x: 1$$ where $$x=$$ ________.
Each of three blocks $$\mathrm{P}, \mathrm{Q}$$ and $$\mathrm{R}$$ shown in figure has a mass of $$3 \mathrm{~kg}$$. Each of the wires $$\mathrm{A}$$ and $$\mathrm{B}$$ has cross-sectional area $$0.005 \mathrm{~cm}^2$$ and Young's modulus $$2 \times 10^{11} \mathrm{~N} \mathrm{~m}^{-2}$$. Neglecting friction, the longitudinal strain on wire $$B$$ is ________ $$\times 10^{-4}$$. (Take $$\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$$)

Two metallic wires $$P$$ and $$Q$$ have same volume and are made up of same material. If their area of cross sections are in the ratio $$4: 1$$ and force $$F_1$$ is applied to $$P$$, an extension of $$\Delta l$$ is produced. The force which is required to produce same extension in $$Q$$ is $$\mathrm{F}_2$$.
The value of $$\frac{F_1}{F_2}$$ is _________.
In a test experiment on a model aeroplane in wind tunnel, the flow speeds on the upper and lower surfaces of the wings are $$70 \mathrm{~ms}^{-1}$$ and $$65 \mathrm{~ms}^{-1}$$ respectively. If the wing area is $$2 \mathrm{~m}^2$$, the lift of the wing is _________ $$N$$.
(Given density of air $$=1.2 \mathrm{~kg} \mathrm{~m}^{-3}$$)
The reading of pressure metre attached with a closed pipe is $$4.5 \times 10^4 \mathrm{~N} / \mathrm{m}^2$$. On opening the valve, water starts flowing and the reading of pressure metre falls to $$2.0 \times 10^4 \mathrm{~N} / \mathrm{m}^2$$. The velocity of water is found to be $$\sqrt{V} \mathrm{~m} / \mathrm{s}$$. The value of $$V$$ is _________.
If average depth of an ocean is $$4000 \mathrm{~m}$$ and the bulk modulus of water is $$2 \times 10^9 \mathrm{~Nm}^{-2}$$, then fractional compression $$\frac{\Delta V}{V}$$ of water at the bottom of ocean is $$\alpha \times 10^{-2}$$. The value of $$\alpha$$ is _______ (Given, $$\mathrm{g}=10 \mathrm{~ms}^{-2}, \rho=1000 \mathrm{~kg} \mathrm{~m}^{-3}$$)
The elastic potential energy stored in a steel wire of length $$20 \mathrm{~m}$$ stretched through $$2 \mathrm{~cm}$$ is $$80 \mathrm{~J}$$. The cross sectional area of the wire is __________ $$\mathrm{mm}^{2}$$.
$$\left(\right.$$ Given, $$\left.y=2.0 \times 10^{11} \mathrm{Nm}^{-2}\right)$$
Glycerin of density $$1.25 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3}$$ is flowing through the conical section of pipe The area of cross-section of the pipe at its ends are $$10 \mathrm{~cm}^{2}$$ and $$5 \mathrm{~cm}^{2}$$ and pressure drop across its length is $$3 ~\mathrm{Nm}^{-2}$$. The rate of flow of glycerin through the pipe is $$x \times 10^{-5} \mathrm{~m}^{3} \mathrm{~s}^{-1}$$. The value of $$x$$ is ___________.
The surface tension of soap solution is $$3.5 \times 10^{-2} \mathrm{~Nm}^{-1}$$. The amount of work done required to increase the radius of soap bubble from $$10 \mathrm{~cm}$$ to $$20 \mathrm{~cm}$$ is _________ $$\times ~10^{-4} \mathrm{~J}$$.
$$(\operatorname{take} \pi=22 / 7)$$
A wire of density $$8 \times 10^{3} \mathrm{~kg} / \mathrm{m}^{3}$$ is stretched between two clamps $$0.5 \mathrm{~m}$$ apart. The extension developed in the wire is $$3.2 \times 10^{-4} \mathrm{~m}$$. If $$Y=8 \times 10^{10} \mathrm{~N} / \mathrm{m}^{2}$$, the fundamental frequency of vibration in the wire will be ___________ $$\mathrm{Hz}$$.
The length of a wire becomes $$l_{1}$$ and $$l_{2}$$ when $$100 \mathrm{~N}$$ and $$120 \mathrm{~N}$$ tensions are applied respectively. If $$10 ~l_{2}=11~ l_{1}$$, the natural length of wire will be $$\frac{1}{x} ~l_{1}$$. Here the value of $$x$$ is _____________.
Figure below shows a liquid being pushed out of the tube by a piston having area of cross section $$2.0 \mathrm{~cm}^{2}$$. The area of cross section at the outlet is $$10 \mathrm{~mm}^{2}$$. If the piston is pushed at a speed of $$4 \mathrm{~cm} \mathrm{~s}^{-1}$$, the speed of outgoing fluid is __________ $$\mathrm{cm} \mathrm{s}^{-1}$$

Two wires each of radius 0.2 cm and negligible mass, one made of steel and the other made of brass are loaded as shown in the figure. The elongation of the steel wire is __________ $$\times$$ 10$$^{-6}$$ m. [Young's modulus for steel = 2 $$\times$$ 10$$^{11}$$ Nm$$^{-2}$$ and g = 10 ms$$^{-2}$$ ]

An air bubble of diameter $$6 \mathrm{~mm}$$ rises steadily through a solution of density $$1750 \mathrm{~kg} / \mathrm{m}^{3}$$ at the rate of $$0.35 \mathrm{~cm} / \mathrm{s}$$. The co-efficient of viscosity of the solution (neglect density of air) is ___________ Pas (given, $$\mathrm{g}=10 \mathrm{~ms}^{-2}$$ ).
A metal block of mass $$\mathrm{m}$$ is suspended from a rigid support through a metal wire of diameter $$14 \mathrm{~mm}$$. The tensile stress developed in the wire under equilibrium state is $$7 \times 10^{5} \mathrm{Nm}^{-2}$$. The value of mass $$\mathrm{m}$$ is _________ $$\mathrm{kg}$$. (Take, $$\mathrm{g}=9.8 \mathrm{~ms}^{-2}$$ and $$\pi=\frac{22}{7}$$ )
A steel rod has a radius of $$20 \mathrm{~mm}$$ and a length of $$2.0 \mathrm{~m}$$. A force of $$62.8 ~\mathrm{kN}$$ stretches it along its length. Young's modulus of steel is $$2.0 \times 10^{11} \mathrm{~N} / \mathrm{m}^{2}$$. The longitudinal strain produced in the wire is _____________ $$\times 10^{-5}$$
The surface of water in a water tank of cross section area $$750 \mathrm{~cm}^{2}$$ on the top of a house is $$h \mathrm{~m}$$ above the tap level. The speed of water coming out through the tap of cross section area $$500 \mathrm{~mm}^{2}$$ is $$30 \mathrm{~cm} / \mathrm{s}$$. At that instant, $$\frac{d h}{d t}$$ is $$x \times 10^{-3} \mathrm{~m} / \mathrm{s}$$. The value of $$x$$ will be ____________.
A certain pressure '$$\mathrm{P}$$' is applied to 1 litre of water and 2 litre of a liquid separately. Water gets compressed to $$0.01 \%$$ whereas the liquid gets compressed to $$0.03 \%$$. The ratio of Bulk modulus of water to that of the liquid is $$\frac{3}{x}$$. The value of $$x$$ is ____________.
A thin rod having a length of $$1 \mathrm{~m}$$ and area of cross-section $$3 \times 10^{-6} \mathrm{~m}^{2}$$ is suspended vertically from one end. The rod is cooled from $$210^{\circ} \mathrm{C}$$ to $$160^{\circ} \mathrm{C}$$. After cooling, a mass $$\mathrm{M}$$ is attached at the lower end of the rod such that the length of rod again becomes $$1 \mathrm{~m}$$. Young's modulus and coefficient of linear expansion of the rod are $$2 \times 10^{11} \mathrm{~N} \mathrm{~m}^{-2}$$ and $$2 \times 10^{-5} \mathrm{~K}^{-1}$$, respectively. The value of $$\mathrm{M}$$ is __________ $$\mathrm{kg}$$.
(Take $$\mathrm{g=10~m~s^{-2}}$$)
A metal block of base area 0.20 m$$^2$$ is placed on a table, as shown in figure. A liquid film of thickness 0.25 mm is inserted between the block and the table. The block is pushed by a horizontal force of 0.1 N and moves with a constant speed. IF the viscosity of the liquid is $$5.0\times10^{-3}~\mathrm{Pl}$$, the speed of block is ____________ $$\times10^{-3}$$ m/s.

A body cools from 60$$^\circ$$C to 40$$^\circ$$C in 6 minutes. If, temperature of surroundings is 10$$^\circ$$C. Then, after the next 6 minutes, its temperature will be ____________$$^\circ$$C.
A spherical drop of liquid splits into 1000 identical spherical drops. If u$$_\mathrm{i}$$ is the surface energy of the original drop and u$$_\mathrm{f}$$ is the total surface energy of the resulting drops, the (ignoring evaporation), $${{{u_f}} \over {{u_i}}} = \left( {{{10} \over x}} \right)$$. Then value of x is ____________ :
As shown in the figure, in an experiment to determine Young's modulus of a wire, the extension-load curve is plotted. The curve is a straight line passing through the origin and makes an angle of 45$$^\circ$$ with the load axis. The length of wire is 62.8 cm and its diameter is 4 mm. The Young's modulus is found to be $$x\times10^4$$ Nm$$^{-2}$$. The value of $$x$$ is ___________.

A Spherical ball of radius 1mm and density 10.5 g/cc is dropped in glycerine of coefficient of viscosity 9.8 poise and density 1.5 g/cc. Viscous force on the ball when it attains constant velocity is $$3696\times10^{-x}$$ N. The value of $$x$$ is ________.
(Given, g = 9.8 m/s$$^2$$ and $$\pi=\frac{22}{7}$$)
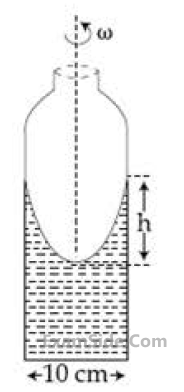
A tube of length $$50 \mathrm{~cm}$$ is filled completely with an incompressible liquid of mass $$250 \mathrm{~g}$$ and closed at both ends. The tube is then rotated in horizontal plane about one of its ends with a uniform angular velocity $$x \sqrt{F} \,\mathrm{rad} \,\mathrm{s}^{-1}$$. If $$\mathrm{F}$$ be the force exerted by the liquid at the other end then the value of $$x$$ will be __________.
A metal wire of length $$0.5 \mathrm{~m}$$ and cross-sectional area $$10^{-4} \mathrm{~m}^{2}$$ has breaking stress $$5 \times 10^{8} \,\mathrm{Nm}^{-2}$$. A block of $$10 \mathrm{~kg}$$ is attached at one end of the string and is rotating in a horizontal circle. The maximum linear velocity of block will be _________ $$\mathrm{ms}^{-1}$$.
The velocity of a small ball of mass $$0.3 \mathrm{~g}$$ and density $$8 \mathrm{~g} / \mathrm{cc}$$ when dropped in a container filled with glycerine becomes constant after some time. If the density of glycerine is $$1.3 \mathrm{~g} / \mathrm{cc}$$, then the value of viscous force acting on the ball will be $$x \times 10^{-4} \mathrm{~N}$$, The value of $$x$$ is _________. [use $$\left.\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right]$$
The speed of a transverse wave passing through a string of length $$50 \mathrm{~cm}$$ and mass $$10 \mathrm{~g}$$ is $$60 \mathrm{~ms}^{-1}$$. The area of cross-section of the wire is $$2.0 \mathrm{~mm}^{2}$$ and its Young's modulus is $$1.2 \times 10^{11} \mathrm{Nm}^{-2}$$. The extension of the wire over its natural length due to its tension will be $$x \times 10^{-5} \mathrm{~m}$$. The value of $$x$$ is __________.
A string of area of cross-section $$4 \mathrm{~mm}^{2}$$ and length $$0.5 \mathrm{~m}$$ is connected with a rigid body of mass $$2 \mathrm{~kg}$$. The body is rotated in a vertical circular path of radius $$0.5 \mathrm{~m}$$. The body acquires a speed of $$5 \mathrm{~m} / \mathrm{s}$$ at the bottom of the circular path. Strain produced in the string when the body is at the bottom of the circle is _________ $$ \times 10^{-5}$$.
(use Young's modulus $$10^{11} \mathrm{~N} / \mathrm{m}^{2}$$ and $$\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}$$)
The diameter of an air bubble which was initially $$2 \mathrm{~mm}$$, rises steadily through a solution of density $$1750 \mathrm{~kg} \mathrm{~m}^{-3}$$ at the rate of $$0.35 \,\mathrm{cms}^{-1}$$. The coefficient of viscosity of the solution is _________ poise (in nearest integer). (the density of air is negligible).
In an experiment to determine the Young's modulus, steel wires of five different lengths $$(1,2,3,4$$, and $$5 \mathrm{~m})$$ but of same cross section $$\left(2 \mathrm{~mm}^{2}\right)$$ were taken and curves between extension and load were obtained. The slope (extension/load) of the curves were plotted with the wire length and the following graph is obtained. If the Young's modulus of given steel wires is $$x \times 10^{11} \,\mathrm{Nm}^{-2}$$, then the value of $$x$$ is __________.

A spherical soap bubble of radius 3 cm is formed inside another spherical soap bubble of radius 6 cm. If the internal pressure of the smaller bubble of radius 3 cm in the above system is equal to the internal pressure of the another single soap bubble of radius r cm. The value of r is ___________.
A square aluminum (shear modulus is $$25 \times 10^{9}\, \mathrm{Nm}^{-2}$$) slab of side $$60 \mathrm{~cm}$$ and thickness $$15 \mathrm{~cm}$$ is subjected to a shearing force (on its narrow face) of $$18.0 \times 10^{4}$$ $$\mathrm{N}$$. The lower edge is riveted to the floor. The displacement of the upper edge is ____________ $$\mu$$m.
A uniform heavy rod of mass $$20 \mathrm{~kg}$$, cross sectional area $$0.4 \mathrm{~m}^{2}$$ and length $$20 \mathrm{~m}$$ is hanging from a fixed support. Neglecting the lateral contraction, the elongation in the rod due to its own weight is $$x \times 10^{-9} \mathrm{~m}$$. The value of $$x$$ is _______________.
(Given, young modulus Y = 2 $$\times$$ 1011 Nm$$-$$2 and g = 10 ms$$-$$2)
In an experiment to determine the Young's modulus of wire of a length exactly $$1 \mathrm{~m}$$, the extension in the length of the wire is measured as $$0.4 \mathrm{~mm}$$ with an uncertainty of $$\pm\, 0.02 \mathrm{~mm}$$ when a load of $$1 \mathrm{~kg}$$ is applied. The diameter of the wire is measured as $$0.4 \mathrm{~mm}$$ with an uncertainty of $$\pm \,0.01 \mathrm{~mm}$$. The error in the measurement of Young's modulus $$(\Delta \mathrm{Y})$$ is found to be $$x \times 10^{10}\, \mathrm{Nm}^{-2}$$. The value of $$x$$ is _________________. $$\left(\right.$$take $$\mathrm{g}=10 \mathrm{~ms}^{-2}$$ )
A wire of length $$\mathrm{L}$$ and radius $$\mathrm{r}$$ is clamped rigidly at one end. When the other end of the wire is pulled by a force $$\mathrm{F}$$, its length increases by $$5 \mathrm{~cm}$$. Another wire of the same material of length $$4 \mathrm{L}$$ and radius $$4 \mathrm{r}$$ is pulled by a force $$4 \mathrm{F}$$ under same conditions. The increase in length of this wire is __________________ $$\mathrm{cm}$$.
The excess pressure inside a liquid drop is 500 Nm$$-$$2. If the radius of the drop is 2 mm, the surface tension of liquid is x $$\times$$ 10$$-$$3 Nm$$-$$1. The value of x is _____________.
A small spherical ball of radius 0.1 mm and density 104 kg m$$-$$3 falls freely under gravity through a distance h before entering a tank of water. If, after entering the water the velocity of ball does not change and it continue to fall with same constant velocity inside water, then the value of h will be ___________ m.
(Given g = 10 ms$$-$$2, viscosity of water = 1.0 $$\times$$ 10$$-$$5 N-sm$$-$$2).
A liquid of density 750 kgm$$-$$3 flows smoothly through a horizontal pipe that tapers in cross-sectional area from A1 = 1.2 $$\times$$ 10$$-$$2 m2 to A2 = $${{{A_1}} \over 2}$$. The pressure difference between the wide and narrow sections of the pipe is 4500 Pa. The rate of flow of liquid is ___________ $$\times$$ 10$$-$$3 m3s$$-$$1.
The area of cross-section of a large tank is 0.5 m2. It has a narrow opening near the bottom having area of cross-section 1 cm2. A load of 25 kg is applied on the water at the top in the tank. Neglecting the speed of water in the tank, the velocity of the water, coming out of the opening at the time when the height of water level in the tank is 40 cm above the bottom, will be ___________ cms$$-$$1. [Take g = 10 ms$$-$$2]
The elastic behaviour of material for linear stress and linear strain, is shown in the figure. The energy density for a linear strain of 5 $$\times$$ 10$$-$$4 is __________ kJ/m3. Assume that material is elastic upto the linear strain of 5 $$\times$$ 10$$-$$4.

The elongation of a wire on the surface of the earth is 10$$-$$4 m. The same wire of same dimensions is elongated by 6 $$\times$$ 10$$-$$5 m on another planet. The acceleration due to gravity on the planet will be ____________ ms$$-$$2. (Take acceleration due to gravity on the surface of earth = 10 ms$$-$$2)
An ideal fluid of density 800 kgm$$-$$3, flows smoothly through a bent pipe (as shown in figure) that tapers in cross-sectional area from a to $${a \over 2}$$. The pressure difference between the wide and narrow sections of pipe is 4100 Pa. At wider section, the velocity of fluid is $${{\sqrt x } \over 6}$$ ms$$-$$1 for x = ___________. (Given g = 10 ms$$-$$2)

The velocity of upper layer of water in a river is 36 kmh$$-$$1. Shearing stress between horizontal layers of water is 10$$-$$3 Nm$$-$$2. Depth of the river is __________ m. (Co-efficient of viscosity of water is 10$$-$$2 Pa.s)
In an experiment to verify Newton's law of cooling, a graph is plotted between the temperature difference ($$\Delta$$T) of the water and surroundings and time as shown in figure. The initial temperature of water is taken as 80$$^\circ$$C. The value of t2 as mentioned in the graph will be __________.

(The bulk modulus of rubber = 9.8 $$\times$$ 108 Nm$$-$$2, Density of sea water = 103 kgm$$-$$3, g = 9.8 m/s2)
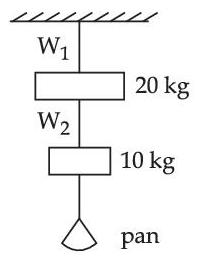
(Young's modulus of rubber = 0.5 $$\times$$ 109 N/m2)
The value of v, to the nearest integer, is ___________. [Take value of g to be 10 ms-2]
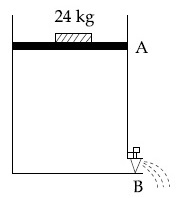
(Give answer in closest integer) _____.