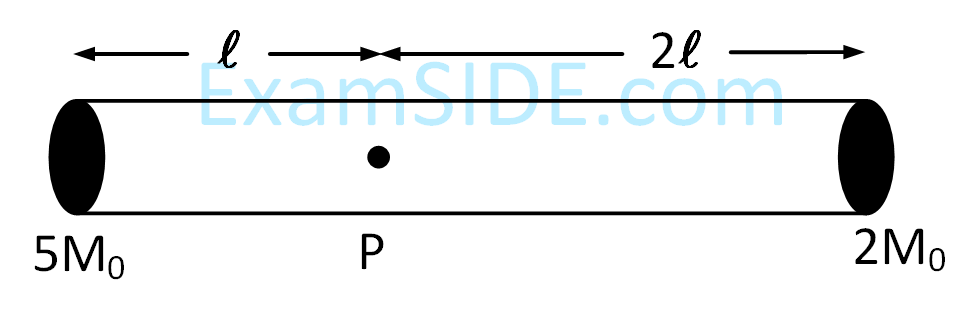
A rigid massless rod of length 3l has two masses attached at each end as shown in the figure. The rod is pivoted at point P on the horizontal axis (see figure). When released from initial horizontal position, its instantaneous angular acceleration will be -

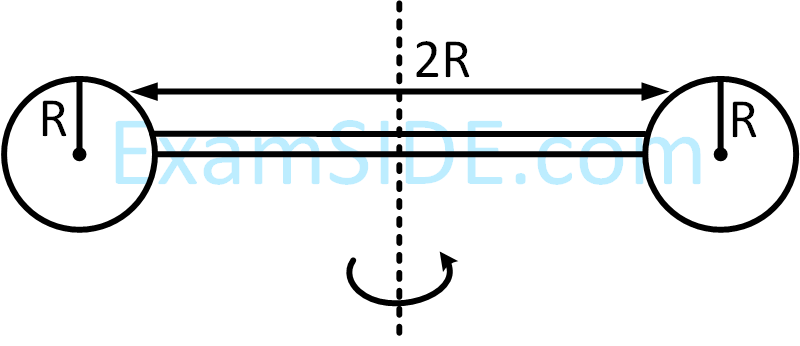
Two identical spherical balls of mass M and radius R each are stuck on two ends of a rod of length 2R and mass M (see figure). The moment of inertia of the system about the axis passing perpendicularly through the centre of the rod is :

To mop-clean a floor, a cleaning machine presses a circular mop of radius R vertically down with a total force F and rotates it with a constant angular speed about its axis. If the force F is distributed uniformly over the mop and if coefficient of friction between the mop and the floor is $$\mu $$, the torque, applied by the machine on the mop is -

A homogeneous solid cylindrical roller of radius R and mass M is pulled on a cricket pitch by a horizontal force. Assuming rolling without slipping, angular acceleration of the cylinder is -