
Wheatstone bridge principle is used to measure the specific resistance $$\left(S_1\right)$$ of given wire, having length $$L$$, radius $$r$$. If $$X$$ is the resistance of wire, then specific resistance is ; $$S_1=X\left(\frac{\pi r^2}{L}\right)$$. If the length of the wire gets doubled then the value of specific resistance will be :

A wire of length $$10 \mathrm{~cm}$$ and radius $$\sqrt{7} \times 10^{-4} \mathrm{~m}$$ connected across the right gap of a meter bridge. When a resistance of $$4.5 \Omega$$ is connected on the left gap by using a resistance box, the balance length is found to be at $$60 \mathrm{~cm}$$ from the left end. If the resistivity of the wire is $$\mathrm{R} \times 10^{-7} \Omega \mathrm{m}$$, then value of $$\mathrm{R}$$ is :

A wire of resistance $$\mathrm{R}$$ and length $$\mathrm{L}$$ is cut into 5 equal parts. If these parts are joined parallely, then resultant resistance will be :

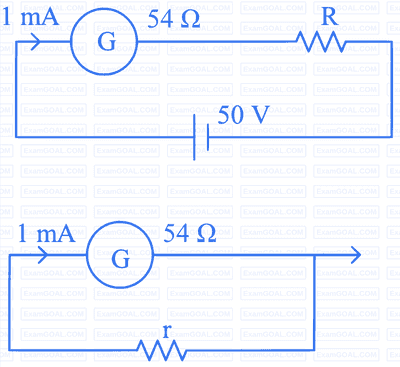
(A) for voltmeter $R \approx 50 \mathrm{k} \Omega$
(B) for ammeter $\mathrm{r} \approx 0.2 \Omega$
(C) for ammeter $\mathrm{r}=6 \Omega$
(D) for voltmeter $R \approx 5 \mathrm{k} \Omega$
(E) for voltmeter $R \approx 500 \Omega$
Choose the correct answer from the options given below: