1
JEE Main 2021 (Online) 25th July Evening Shift
MCQ (Single Correct Answer)
+4
-1

Let X be a random variable such that the probability function of a distribution is given by $$P(X = 0) = {1 \over 2},P(X = j) = {1 \over {{3^j}}}(j = 1,2,3,...,\infty )$$. Then the mean of the distribution and P(X is positive and even) respectively are :
2
JEE Main 2021 (Online) 25th July Evening Shift
MCQ (Single Correct Answer)
+4
-1

If $${}^n{P_r} = {}^n{P_{r + 1}}$$ and $${}^n{C_r} = {}^n{C_{r - 1}}$$, then the value of r is equal to :
3
JEE Main 2021 (Online) 25th July Evening Shift
MCQ (Single Correct Answer)
+4
-1

Let y = y(x) be the solution of the differential
equation xdy = (y + x3 cosx)dx with y($$\pi$$) = 0, then $$y\left( {{\pi \over 2}} \right)$$ is equal to :
equation xdy = (y + x3 cosx)dx with y($$\pi$$) = 0, then $$y\left( {{\pi \over 2}} \right)$$ is equal to :
4
JEE Main 2021 (Online) 25th July Evening Shift
Numerical
+4
-1

Consider the function
where P(x) is a polynomial such that P'' (x) is always a constant and P(3) = 9. If f(x) is continuous at x = 2, then P(5) is equal to _____________.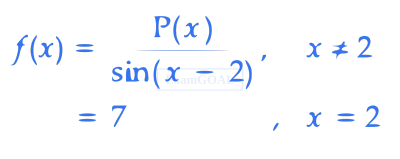
where P(x) is a polynomial such that P'' (x) is always a constant and P(3) = 9. If f(x) is continuous at x = 2, then P(5) is equal to _____________.
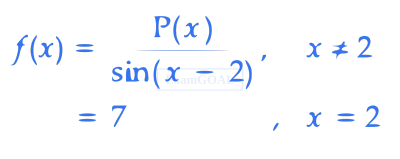
Your input ____
Paper analysis
Total Questions
Chemistry
23
Mathematics
23
Physics
25
More papers of JEE Main
JEE Main 2025 (Online) 8th April Evening Shift
JEE Main 2025 (Online) 7th April Evening Shift
JEE Main 2025 (Online) 7th April Morning Shift
JEE Main 2025 (Online) 4th April Evening Shift
JEE Main 2025 (Online) 4th April Morning Shift
JEE Main 2025 (Online) 3rd April Evening Shift
JEE Main 2025 (Online) 3rd April Morning Shift
JEE Main 2025 (Online) 2nd April Evening Shift
JEE Main 2025 (Online) 2nd April Morning Shift
JEE Main 2025 (Online) 29th January Evening Shift
JEE Main 2025 (Online) 29th January Morning Shift
JEE Main 2025 (Online) 28th January Evening Shift
JEE Main 2025 (Online) 28th January Morning Shift
JEE Main 2025 (Online) 24th January Evening Shift
JEE Main 2025 (Online) 24th January Morning Shift
JEE Main 2025 (Online) 23rd January Evening Shift
JEE Main 2025 (Online) 23rd January Morning Shift
JEE Main 2025 (Online) 22nd January Evening Shift
JEE Main 2025 (Online) 22nd January Morning Shift
JEE Main 2024 (Online) 9th April Evening Shift
JEE Main 2024 (Online) 9th April Morning Shift
JEE Main 2024 (Online) 8th April Evening Shift
JEE Main 2024 (Online) 8th April Morning Shift
JEE Main 2024 (Online) 6th April Evening Shift
JEE Main 2024 (Online) 6th April Morning Shift
JEE Main 2024 (Online) 5th April Evening Shift
JEE Main 2024 (Online) 5th April Morning Shift
JEE Main 2024 (Online) 4th April Evening Shift
JEE Main 2024 (Online) 4th April Morning Shift
JEE Main 2024 (Online) 1st February Evening Shift
JEE Main 2024 (Online) 1st February Morning Shift
JEE Main 2024 (Online) 31st January Evening Shift
JEE Main 2024 (Online) 31st January Morning Shift
JEE Main 2024 (Online) 30th January Evening Shift
JEE Main 2024 (Online) 30th January Morning Shift
JEE Main 2024 (Online) 29th January Evening Shift
JEE Main 2024 (Online) 29th January Morning Shift
JEE Main 2024 (Online) 27th January Evening Shift
JEE Main 2024 (Online) 27th January Morning Shift
JEE Main 2023 (Online) 15th April Morning Shift
JEE Main 2023 (Online) 13th April Evening Shift
JEE Main 2023 (Online) 13th April Morning Shift
JEE Main 2023 (Online) 12th April Morning Shift
JEE Main 2023 (Online) 11th April Evening Shift
JEE Main 2023 (Online) 11th April Morning Shift
JEE Main 2023 (Online) 10th April Evening Shift
JEE Main 2023 (Online) 10th April Morning Shift
JEE Main 2023 (Online) 8th April Evening Shift
JEE Main 2023 (Online) 8th April Morning Shift
JEE Main 2023 (Online) 6th April Evening Shift
JEE Main 2023 (Online) 6th April Morning Shift
JEE Main 2023 (Online) 1st February Evening Shift
JEE Main 2023 (Online) 1st February Morning Shift
JEE Main 2023 (Online) 31st January Evening Shift
JEE Main 2023 (Online) 31st January Morning Shift
JEE Main 2023 (Online) 30th January Evening Shift
JEE Main 2023 (Online) 30th January Morning Shift
JEE Main 2023 (Online) 29th January Evening Shift
JEE Main 2023 (Online) 29th January Morning Shift
JEE Main 2023 (Online) 25th January Evening Shift
JEE Main 2023 (Online) 25th January Morning Shift
JEE Main 2023 (Online) 24th January Evening Shift
JEE Main 2023 (Online) 24th January Morning Shift
JEE Main 2022 (Online) 29th July Evening Shift
JEE Main 2022 (Online) 29th July Morning Shift
JEE Main 2022 (Online) 28th July Evening Shift
JEE Main 2022 (Online) 28th July Morning Shift
JEE Main 2022 (Online) 27th July Evening Shift
JEE Main 2022 (Online) 27th July Morning Shift
JEE Main 2022 (Online) 26th July Evening Shift
JEE Main 2022 (Online) 26th July Morning Shift
JEE Main 2022 (Online) 25th July Evening Shift
JEE Main 2022 (Online) 25th July Morning Shift
JEE Main 2022 (Online) 30th June Morning Shift
JEE Main 2022 (Online) 29th June Evening Shift
JEE Main 2022 (Online) 29th June Morning Shift
JEE Main 2022 (Online) 28th June Evening Shift
JEE Main 2022 (Online) 28th June Morning Shift
JEE Main 2022 (Online) 27th June Evening Shift
JEE Main 2022 (Online) 27th June Morning Shift
JEE Main 2022 (Online) 26th June Evening Shift
JEE Main 2022 (Online) 26th June Morning Shift
JEE Main 2022 (Online) 25th June Evening Shift
JEE Main 2022 (Online) 25th June Morning Shift
JEE Main 2022 (Online) 24th June Evening Shift
JEE Main 2022 (Online) 24th June Morning Shift
JEE Main 2021 (Online) 1st September Evening Shift
JEE Main 2021 (Online) 31st August Evening Shift
JEE Main 2021 (Online) 31st August Morning Shift
JEE Main 2021 (Online) 27th August Evening Shift
JEE Main 2021 (Online) 27th August Morning Shift
JEE Main 2021 (Online) 26th August Evening Shift
JEE Main 2021 (Online) 26th August Morning Shift
JEE Main 2021 (Online) 27th July Evening Shift
JEE Main 2021 (Online) 27th July Morning Shift
JEE Main 2021 (Online) 25th July Evening Shift
JEE Main 2021 (Online) 25th July Morning Shift
JEE Main 2021 (Online) 22th July Evening Shift
JEE Main 2021 (Online) 20th July Evening Shift
JEE Main 2021 (Online) 20th July Morning Shift
JEE Main 2021 (Online) 18th March Evening Shift
JEE Main 2021 (Online) 18th March Morning Shift
JEE Main 2021 (Online) 17th March Evening Shift
JEE Main 2021 (Online) 17th March Morning Shift
JEE Main 2021 (Online) 16th March Evening Shift
JEE Main 2021 (Online) 16th March Morning Shift
JEE Main 2021 (Online) 26th February Evening Shift
JEE Main 2021 (Online) 26th February Morning Shift
JEE Main 2021 (Online) 25th February Evening Shift
JEE Main 2021 (Online) 25th February Morning Shift
JEE Main 2021 (Online) 24th February Evening Shift
JEE Main 2021 (Online) 24th February Morning Shift
JEE Main 2020 (Online) 6th September Evening Slot
JEE Main 2020 (Online) 6th September Morning Slot
JEE Main 2020 (Online) 5th September Evening Slot
JEE Main 2020 (Online) 5th September Morning Slot
JEE Main 2020 (Online) 4th September Evening Slot
JEE Main 2020 (Online) 4th September Morning Slot
JEE Main 2020 (Online) 3rd September Evening Slot
JEE Main 2020 (Online) 3rd September Morning Slot
JEE Main 2020 (Online) 2nd September Evening Slot
JEE Main 2020 (Online) 2nd September Morning Slot
JEE Main 2020 (Online) 9th January Evening Slot
JEE Main 2020 (Online) 9th January Morning Slot
JEE Main 2020 (Online) 8th January Evening Slot
JEE Main 2020 (Online) 8th January Morning Slot
JEE Main 2020 (Online) 7th January Evening Slot
JEE Main 2020 (Online) 7th January Morning Slot
JEE Main 2019 (Online) 12th April Evening Slot
JEE Main 2019 (Online) 12th April Morning Slot
JEE Main 2019 (Online) 10th April Evening Slot
JEE Main 2019 (Online) 10th April Morning Slot
JEE Main 2019 (Online) 9th April Evening Slot
JEE Main 2019 (Online) 9th April Morning Slot
JEE Main 2019 (Online) 8th April Evening Slot
JEE Main 2019 (Online) 8th April Morning Slot
JEE Main 2019 (Online) 12th January Evening Slot
JEE Main 2019 (Online) 12th January Morning Slot
JEE Main 2019 (Online) 11th January Evening Slot
JEE Main 2019 (Online) 11th January Morning Slot
JEE Main 2019 (Online) 10th January Evening Slot
JEE Main 2019 (Online) 10th January Morning Slot
JEE Main 2019 (Online) 9th January Evening Slot
JEE Main 2019 (Online) 9th January Morning Slot
JEE Main 2018 (Online) 16th April Morning Slot
JEE Main 2018 (Offline)
JEE Main 2018 (Online) 15th April Evening Slot
JEE Main 2018 (Online) 15th April Morning Slot
JEE Main 2017 (Online) 9th April Morning Slot
JEE Main 2017 (Online) 8th April Morning Slot
JEE Main 2017 (Offline)
JEE Main 2016 (Online) 10th April Morning Slot
JEE Main 2016 (Online) 9th April Morning Slot
JEE Main 2016 (Offline)
JEE Main 2015 (Offline)
JEE Main 2014 (Offline)
JEE Main 2013 (Offline)
AIEEE 2012
AIEEE 2011
AIEEE 2010
AIEEE 2009
AIEEE 2008
AIEEE 2007
AIEEE 2006
AIEEE 2005
AIEEE 2004
AIEEE 2003
AIEEE 2002
JEE Main
Papers
2025
2024
2023
2022
2021
2020
2019
2018
2017
2016
2012
2011
2010
2009
2008
2007
2006
2005
2004
2003
2002