Consider the system of linear equations

$$-$$x + y + 2z = 0

3x $$-$$ ay + 5z = 1

2x $$-$$ 2y $$-$$ az = 7

Let S₁ be the set of all a$$\in$$R for which the system is inconsistent and S₂ be the set of all a$$\in$$R for which the system has infinitely many solutions. If n(S₁) and n(S₂) denote the number of elements in S₁ and S₂ respectively, then

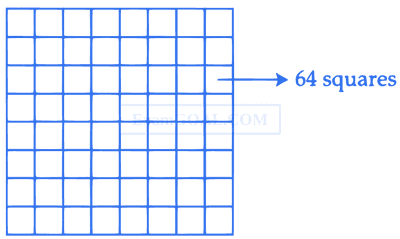
Two squares are chosen at random on a chessboard (see figure). The probability that they have a side in common is :

If y = y(x) is the solution curve of the differential equation $${x^2}dy + \left( {y - {1 \over x}} \right)dx = 0$$ ; x > 0 and y(1) = 1, then $$y\left( {{1 \over 2}} \right)$$ is equal to :

The function $$f(x) = {x^3} - 6{x^2} + ax + b$$ is such that $$f(2) = f(4) = 0$$. Consider two statements :

Statement 1 : there exists x₁, x₂ $$\in$$(2, 4), x₁ < x₂, such that f'(x₁) = $$-$$1 and f'(x₂) = 0.

Statement 2 : there exists x₃, x₄ $$\in$$ (2, 4), x₃ < x₄, such that f is decreasing in (2, x₄), increasing in (x₄, 4) and $$2f'({x_3}) = \sqrt 3 f({x_4})$$.

Then