1
JEE Main 2021 (Online) 31st August Evening Shift
MCQ (Single Correct Answer)
+4
-1

Statement I :
Two forces $$\left( {\overrightarrow P + \overrightarrow Q } \right)$$ and $$\left( {\overrightarrow P - \overrightarrow Q } \right)$$ where $$\overrightarrow P \bot \overrightarrow Q $$, when act at an angle $$\theta$$1 to each other, the magnitude of their resultant is $$\sqrt {3({P^2} + {Q^2})} $$, when they act at an angle $$\theta$$2, the magnitude of their resultant becomes $$\sqrt {2({P^2} + {Q^2})} $$. This is possible only when $${\theta _1} < {\theta _2}$$.
Statement II :
In the situation given above.
$$\theta$$1 = 60$$^\circ$$ and $$\theta$$2 = 90$$^\circ$$
In the light of the above statements, choose the most appropriate answer from the options given below :-
Two forces $$\left( {\overrightarrow P + \overrightarrow Q } \right)$$ and $$\left( {\overrightarrow P - \overrightarrow Q } \right)$$ where $$\overrightarrow P \bot \overrightarrow Q $$, when act at an angle $$\theta$$1 to each other, the magnitude of their resultant is $$\sqrt {3({P^2} + {Q^2})} $$, when they act at an angle $$\theta$$2, the magnitude of their resultant becomes $$\sqrt {2({P^2} + {Q^2})} $$. This is possible only when $${\theta _1} < {\theta _2}$$.
Statement II :
In the situation given above.
$$\theta$$1 = 60$$^\circ$$ and $$\theta$$2 = 90$$^\circ$$
In the light of the above statements, choose the most appropriate answer from the options given below :-
2
JEE Main 2021 (Online) 27th August Morning Shift
MCQ (Single Correct Answer)
+4
-1

The resultant of these forces $$\overrightarrow {OP} ,\overrightarrow {OQ} ,\overrightarrow {OR} ,\overrightarrow {OS} $$ and $$\overrightarrow {OT} $$ is approximately .......... N.
[Take $$\sqrt 3 = 1.7$$, $$\sqrt 2 = 1.4$$ Given $$\widehat i$$ and $$\widehat j$$ unit vectors along x, y axis]
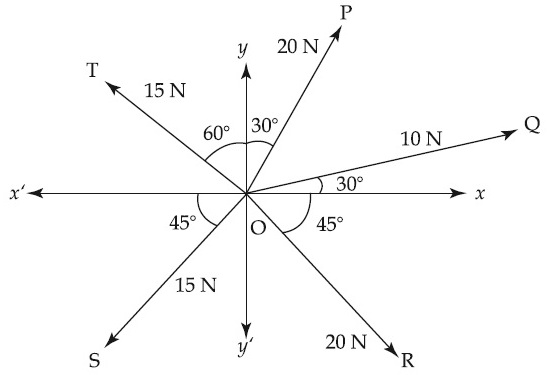
[Take $$\sqrt 3 = 1.7$$, $$\sqrt 2 = 1.4$$ Given $$\widehat i$$ and $$\widehat j$$ unit vectors along x, y axis]

3
JEE Main 2021 (Online) 26th August Evening Shift
MCQ (Single Correct Answer)
+4
-1

The angle between vector $$\left( {\overrightarrow A } \right)$$ and $$\left( {\overrightarrow A - \overrightarrow B } \right)$$ is :
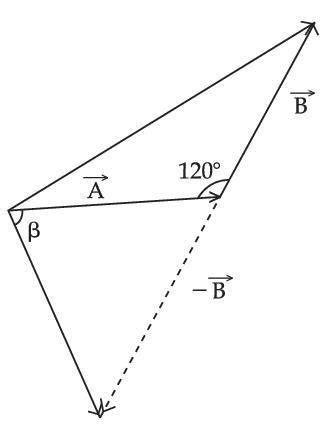

4
JEE Main 2021 (Online) 26th August Morning Shift
MCQ (Single Correct Answer)
+4
-1

The magnitude of vectors $$\overrightarrow {OA} $$, $$\overrightarrow {OB} $$ and $$\overrightarrow {OC} $$ in the given figure are equal. The direction of $$\overrightarrow {OA} $$ + $$\overrightarrow {OB} $$ $$-$$ $$\overrightarrow {OC} $$ with x-axis will be :
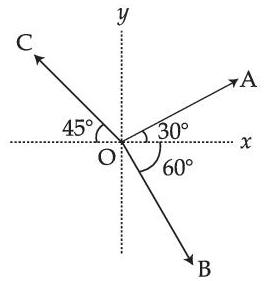

Questions Asked from Vector Algebra (MCQ (Single Correct Answer))
Number in Brackets after Paper Indicates No. of Questions
JEE Main 2024 (Online) 5th April Morning Shift (1)
JEE Main 2024 (Online) 31st January Evening Shift (1)
JEE Main 2023 (Online) 15th April Morning Shift (1)
JEE Main 2023 (Online) 11th April Evening Shift (1)
JEE Main 2023 (Online) 8th April Morning Shift (1)
JEE Main 2023 (Online) 24th January Evening Shift (1)
JEE Main 2022 (Online) 29th June Morning Shift (1)
JEE Main 2022 (Online) 25th June Morning Shift (2)
JEE Main 2021 (Online) 31st August Evening Shift (1)
JEE Main 2021 (Online) 27th August Morning Shift (1)
JEE Main 2021 (Online) 26th August Evening Shift (1)
JEE Main 2021 (Online) 26th August Morning Shift (1)
JEE Main 2021 (Online) 27th July Morning Shift (1)
JEE Main 2021 (Online) 25th July Evening Shift (1)
JEE Main 2021 (Online) 25th July Morning Shift (1)
JEE Main 2021 (Online) 22th July Evening Shift (1)
JEE Main 2021 (Online) 20th July Evening Shift (1)
JEE Main 2021 (Online) 20th July Morning Shift (1)
JEE Main 2021 (Online) 25th February Morning Shift (1)
JEE Main 2019 (Online) 8th April Evening Slot (1)
JEE Main 2019 (Online) 10th January Evening Slot (1)
JEE Main 2019 (Online) 10th January Morning Slot (1)
JEE Main 2018 (Online) 16th April Morning Slot (1)
AIEEE 2004 (1)
JEE Main Subjects
Physics
Mechanics
Units & Measurements Vector Algebra Motion in a Straight Line Motion in a Plane Circular Motion Laws of Motion Work Power & Energy Center of Mass and Collision Rotational Motion Properties of Matter Heat and Thermodynamics Simple Harmonic Motion Waves Gravitation
Electricity
Electrostatics Current Electricity Capacitor Magnetic Effect of Current Magnetic Properties of Matter Electromagnetic Induction Alternating Current Electromagnetic Waves
Optics
Modern Physics
Chemistry
Physical Chemistry
Some Basic Concepts of Chemistry Structure of Atom Redox Reactions Gaseous State Chemical Equilibrium Ionic Equilibrium Solutions Thermodynamics Electrochemistry Chemical Kinetics and Nuclear Chemistry Solid State Surface Chemistry
Inorganic Chemistry
Periodic Table & Periodicity Chemical Bonding & Molecular Structure Isolation of Elements Hydrogen s-Block Elements p-Block Elements d and f Block Elements Coordination Compounds Salt Analysis Environmental Chemistry
Organic Chemistry
Mathematics
Algebra
Sets and Relations Logarithm Quadratic Equation and Inequalities Sequences and Series Mathematical Induction Binomial Theorem Matrices and Determinants Permutations and Combinations Probability Vector Algebra 3D Geometry Complex Numbers Statistics Mathematical Reasoning
Trigonometry
Trigonometric Ratio and Identites Trigonometric Equations Inverse Trigonometric Functions Properties of Triangle Height and Distance
Coordinate Geometry
Calculus