Consider the CMOS circuit shown, where the gate voltage of the n-MOSFET is increased from zero, while the gate voltage of the p-MOSFET is kept constant at 3 V. Assume that, for both transistors, the magnitude of the threshold voltage is 1 V and the product of the transconductance parameter and the $$\left(\frac WL\right)$$ ratio, i.e. the quantity $$\mu C_{ox}\left(\frac WL\right)$$ , is 1 mAV^-2.
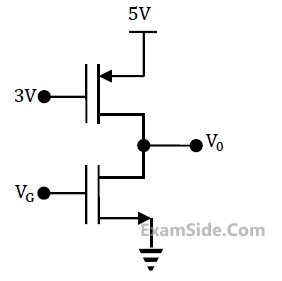
For small increase in V_G beyond 1 V, which of the following gives the correct description of the region of operation of each MOSFET?

The measured transconductance g_m of an NMOS transistor operating in the linear region is plotted against the gate voltage V_G at constant drain voltage V_D. Which of the following figures represents the expected dependence of g_m on V_G?

For the circuit shown in the following figure, transistors M1 and M2 are identical NMOS transistors. Assume that M2 is in saturation and the output is unloaded The current I_x is related to I_bias as

Two identical NMOS transistors M₁ and M₂ are connected as shown below. V_bias is chosen so that both transistors are in saturation. The equivalent g_m of the pair is defined to be $$\frac{\partial I_{out}}{\partial v_i}$$ at constant V_out. The equivalent g_m of the pair is