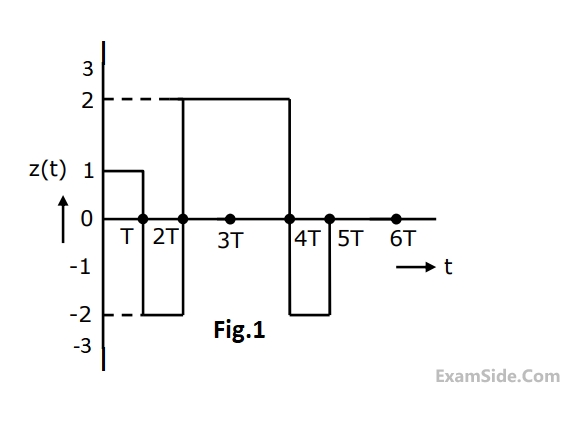
Continuous Time Signal Laplace Transform · Signals and Systems · GATE ECE
Marks 1
Whjen a constant input of value 5 is applied to this filter, the steady state output is ____.
$$I\left( s \right)\,\, = \,{2 \over {s\left( {1 + s} \right)}}$$
As $$t \to \infty $$ , the value of i(t) tends to
Marks 2
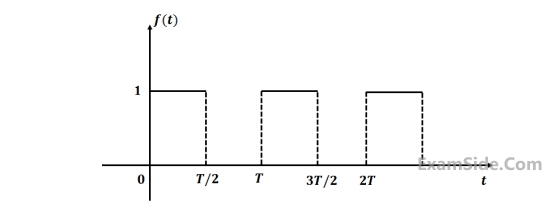
Then the value of β is ______.
Let another signal g(t) be defined as $$\left( t \right) = {\alpha ^2}\int_0^t {h\left( \tau \right)d\tau + {{dh\left( t \right)} \over {dt}} + \alpha h\left( t \right)} $$.
If G(s) is the Laplace transform of g(t), then the number of poles of G(s) is ______.
S1: The system is stable.
S2: $${{h\left( {t + 1} \right)} \over {h\left( t \right)}}$$ is independent of t for t > 0.
S3: A non-casual system with the same transfer function is stable.
For the above system,
When y(0) = 1 and u(t) is a unit step function, y(t) is
Let x(t) be a rectangular pulse given by $$$x\left( t \right) = \left\{ {\matrix{ {1\,\,\,\,\,\,\,\,\,0 \le \,t\, \le 2} \cr {0\,\,\,\,\,otherwise} \cr } } \right.$$$
Assuming that y(0) = 0 $${{dy} \over {dt}} = 0$$ at t = 0, the Laplace transform of y(t) is
The final value of f(t) would be:
is _________. (fill in the blank), n is an integer.
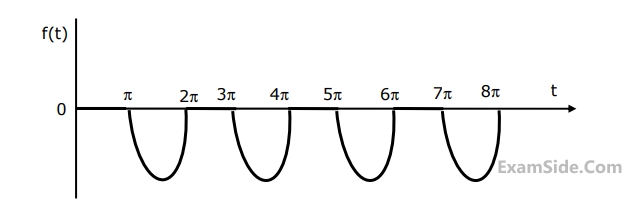
Marks 5
where α is a constant. Determine the value of α.