Representation of Continuous Time Signal Fourier Series · Signals and Systems · GATE ECE

In the table shown below, match the signal type with its spectral characteristics.

	Signal type		Spectral characteristics
(i)	Continuous, aperiodic	(a)	Continuous, aperiodic
(ii)	Continuous, periodic	(b)	Continuous, periodic
(iii)	Discrete, aperiodic	(c)	Discrete, aperiodic
(iv)	Discrete, periodic	(d)	Discrete, periodic

Let 𝑥(𝑡) be a periodic function with period 𝑇 = 10. The Fourier series coefficients for this series are denoted by 𝑎_𝑘, that is

$$x\left( t \right) = \sum\limits_{k = - \infty }^\infty {{a_k}} {e^{jk{{2\pi } \over T}t}}$$

The same function 𝑥(𝑡) can also be considered as a periodic function with period T' = 40. Let b_k be the Fourier series coefficients when period is taken as T'. If $$\sum\limits_{k = - \infty }^\infty {\left| {{a_k}} \right|} = 16$$, then $$\sum\limits_{k = - \infty }^\infty {\left| {{b_k}} \right|} = 16$$ is equal to

Let the input be u and the output be y of a system, and the other parameters are real constants. Identify which among the following systems is not a linear system:

A periodic signal x(t) has a trigonometric Fourier series expansion $$$x\left(t\right)=a_0\;+\;\sum_{n=1}^\infty\left(a_n\cos\;n\omega_0t\;+\;b_n\sin\;n\omega_0t\right)$$$ If $$x\left(t\right)=-x\left(-t\right)=-x\left(t-\mathrm\pi/{\mathrm\omega}_0\right)$$, we can conclude that

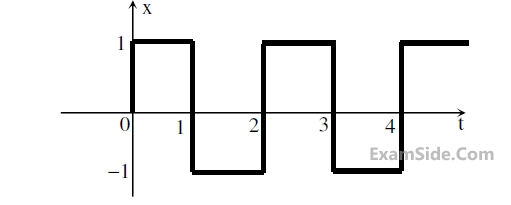Consider the periodic square wave in the figure shown. The ratio of the power in the 7^th harmonic to the power in the 5^th harmonic for this waveform is closest in value to _______.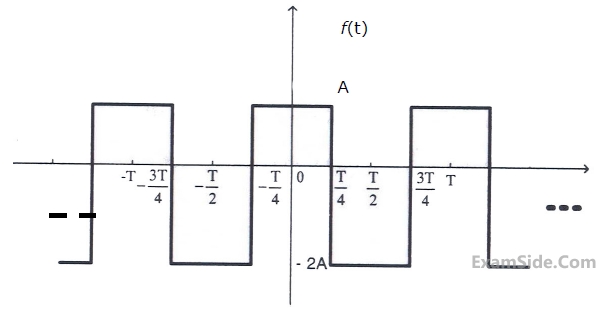

The trigonometric Fourier series for the waveform f(t) shown below contains

The Fourier series of a real periodic function has only

P. Cosine terms if it is even

Q. Sine terms if it is even

R. Cosine terms if it odd

S. Sine terms if it is odd

Which of the above statement are correct?

A function is given by f(t) = sin²t +cos2t . Which of the following is true?

Choose the function f (t );−$$\infty$$ < 1 < +$$\infty$$, for which a Fourier series cannot be defined.

Which of the following cannot be the Fourier series expansion of a periodic signal?

The trigonometric Fourier series of a periodic time function can have only

The trigonometric Fourier series of an even function of time does not have the

The Fourier Series of an odd periodic function, contains only

Let $f(t)$ be a periodic signal with fundamental period $T_0>0$. Consider the signal $y(t)=f(\alpha t)$, where $\alpha>1$.

The Fourier series expansions of $f(t)$ and $y(t)$ are given by

$$ f(t)=\sum\limits_{k = - \infty }^\infty c_k e^{j \frac{2 \pi}{T_0} k T} \text { and } y(t)=\sum\limits_{k = - \infty }^\infty d_k e^{j \frac{2 \pi}{T_0} \alpha k T} . $$

Which of the following statements is/are TRUE?

Let $$\mathrm{x_1(t)=u(t+1.5)-u(t-1.5)}$$ and $$\mathrm{x_2(t)}$$ is shown in the figure below. For $$\mathrm{y(t)=x_1(t)~*~x_2(t)}$$, the $$\int_{ - \infty }^\infty {y(t)dt} $$ is ____________ (rounded off to the nearest integer).

Let x(t) be a continuous time periodic signal with fundamental period T = 1 seconds. Let {a_k} be the complex Fourier series coefficients of x(t), where k is integer valued. Consider the following statements about x(3t):

I. The complex Fourier series coefficients of x(3t) are {a_k} where k is integer valued

II. The complex Fourier series coefficients of x(3t) are {3a_k} where k is integer valued

III. The fundamental angular frequency of x(3t) is 6$$\mathrm\pi$$ rad/s

For the three statements above, which one of the following is correct?

The PSD and the power of a signal g(t) are, respectively, S_g($$\omega$$) and P_g. The PSD and the power of the signal ag(t) are, respectively

Which of the following signals is/are periodic?