State Space Analysis · Control Systems · GATE ECE
Marks 1
1
Consider the state space realization
$$$\left[ {\matrix{
{\mathop x\limits^ \bullet } & {\left( t \right)} \cr
{\mathop x\limits^ \bullet } & {\left( t \right)} \cr
} } \right] = \left[ {\matrix{
0 & 0 \cr
0 & { - 9} \cr
} } \right]\left[ {\matrix{
{{x_1}} & {\left( t \right)} \cr
{{x_2}} & {\left( t \right)} \cr
} } \right] + \left[ {\matrix{
0 \cr
{45} \cr
} } \right]u\left( t \right),$$$ with the initial condition $$\left[ {\matrix{
{{x_1}} & {\left( 0 \right)} \cr
{{x_2}} & {\left( 0 \right)} \cr
} } \right] = \left[ {\matrix{
0 \cr
0 \cr
} } \right];$$
Where u(t) denotes the unit step function.
The value of $$\mathop {Lt}\limits_{x \to \infty } \left| {\sqrt {{x_1}^2\left( t \right) + {x_2}^2\left( t \right)} } \right|$$ is ______
Where u(t) denotes the unit step function.
The value of $$\mathop {Lt}\limits_{x \to \infty } \left| {\sqrt {{x_1}^2\left( t \right) + {x_2}^2\left( t \right)} } \right|$$ is ______
GATE ECE 2017 Set 2
2
Consider the system $${{dx} \over {dt}} = Ax + Bu$$ with $${\rm A} = \left[ {\matrix{
1 & 0 \cr
0 & 1 \cr
} } \right]\,\,\,and\,\,\,{\rm B} = \left[ {\matrix{
p \cr
q \cr
} } \right],$$
where p and q are arbitrary real numbers. Which of the following statesments about the controllability of the system is true?
GATE ECE 2009
3
A linear system is equivalently represented by two sets of state equations. $$\mathop x\limits^ \bullet = \,\,{\rm A}X\,\, + BU$$ and $$\mathop W\limits^ \bullet = \,\,CW\,\, + DU.$$ The eigen values of the representations are also computed as $$\left[ \lambda \right]\,\,\,\,and\,\,\,\,\left[ \mu \right].$$ Which one of the following statements is true?
GATE ECE 2005
4
The transfer function Y(s)/U(s) of a system described by the state equations
$$\mathop x\limits^ \bullet $$(t) = -2x(t)+2u(t)
y(t) = 0.5x(t) is
$$\mathop x\limits^ \bullet $$(t) = -2x(t)+2u(t)
y(t) = 0.5x(t) is
GATE ECE 2002
5
The system mode described by the state equations
$$$X = \left( {\matrix{
0 & 1 \cr
2 & { - 3} \cr
} } \right)x + \left( {\matrix{
0 \cr
1 \cr
} } \right)u,y = \left[ {\matrix{
1 & 1 \cr
} } \right]x$$$
GATE ECE 1999
Marks 2
1
Consider a system $S$ represented in state space as
$$\frac{dx}{dt} = \begin{bmatrix} 0 & -2 \\ 1 & -3 \end{bmatrix}x + \begin{bmatrix} 1 \\ 0 \end{bmatrix}r , \quad y = \begin{bmatrix} 2 & -5 \end{bmatrix}x.$$
Which of the state space representations given below has/have the same transfer function as that of $S$?
GATE ECE 2024
2
The state equation and the output equation of a control system are given below:
$$\mathop x\limits^. = \left[ {\matrix{ { - 4} & { - 1.5} \cr 4 & 0 \cr } } \right]x + \left[ {\matrix{ 2 \cr 0 \cr } } \right]u,$$
$$y = \left[ {\matrix{ {1.5} & {0.625} \cr } } \right]x.$$
The transfer function representation of the system is
$$\mathop x\limits^. = \left[ {\matrix{ { - 4} & { - 1.5} \cr 4 & 0 \cr } } \right]x + \left[ {\matrix{ 2 \cr 0 \cr } } \right]u,$$
$$y = \left[ {\matrix{ {1.5} & {0.625} \cr } } \right]x.$$
The transfer function representation of the system is
GATE ECE 2018
3
A second order LTI system is described by the following state equation.
$$$\eqalign{
& {d \over {dt}}{x_1}\left( t \right) - {x_2}\left( t \right) = 0 \cr
& {d \over {dt}}{x_2}\left( t \right) + 2{x_1}\left( t \right) + 3{x_2}\left( t \right) = r\left( t \right) \cr} $$$
When x1(t) and x2(t) are the two state variables and r(t) denotes the input. The output c(t)=X1(t). The systyem is
GATE ECE 2017 Set 2
4
A second-order linear time-invariant system is described by the following state equations
$$$\eqalign{& {d \over {dt}}{x_1}\left( t \right) + 2{x_1}\left( t \right) = 3u\left( t \right) \cr
& {d \over {dt}}{x_2}\left( t \right) + {x_2}\left( t \right) = u\left( t \right) \cr} $$$
Where x1(t), then the system is
GATE ECE 2016 Set 3
5
The state variable representation of a system is given as
$$$\eqalign{
& \mathop x\limits^ \bullet = \left[ {\matrix{
0 & 1 \cr
0 & { - 1} \cr
} } \right]x;x\left( 0 \right) = \left[ {\matrix{
1 \cr
0 \cr
} } \right] \cr
& y = \left[ {\matrix{
0 & 1 \cr
} } \right]x \cr} $$$
The response y(t) is
GATE ECE 2015 Set 2
6
A network is described by the state model as
$$$\eqalign{
& {\mathop x\limits^ \bullet _1} = 2{x_1} - {x_2} + 3u, \cr
& \mathop {{x_2}}\limits^ \bullet = - 4{x_2} - u, \cr
& y = 3{x_1} - 2{x_2} \cr} $$$
the transfer function H(s)$$\left[ { = {{Y\left( s \right)} \over {U\left( s \right)}}} \right]is$$
GATE ECE 2015 Set 3
7
The state transition matrix $$\phi \left( t \right)$$ of a system $$$\left[ {\matrix{
{\mathop {{x_1}}\limits^ \bullet } \cr
{\mathop {{x_2}}\limits^ \bullet } \cr
} } \right] = \left[ {\matrix{
0 & 1 \cr
0 & 0 \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right] is$$$
GATE ECE 2014 Set 4
8
The state equation of a second-order linear system is given by $$\mathop x\limits^ \bullet \left( t \right) = Ax\left( t \right),x\left( 0 \right) = {x_0}.$$
For $${x_0} = \left[ {\matrix{ 1 \cr { - 1} \cr } } \right],x\left( t \right) = \left[ {\matrix{ {{e^{ - t}}} \cr { - {e^{ - t}}} \cr } } \right]$$ and for $${x_0} = \left[ {\matrix{ 0 \cr 1 \cr } } \right],x\left( t \right) = \left[ {\matrix{ {{e^{ - t}}} & { - {e^{ - 2t}}} \cr { - {e^{ - t}}} & { + 2{e^{ - 2t}}} \cr } } \right]$$ when $${x_0} = \left[ {\matrix{ 3 \cr 5 \cr } } \right],x\left( t \right)$$ is
For $${x_0} = \left[ {\matrix{ 1 \cr { - 1} \cr } } \right],x\left( t \right) = \left[ {\matrix{ {{e^{ - t}}} \cr { - {e^{ - t}}} \cr } } \right]$$ and for $${x_0} = \left[ {\matrix{ 0 \cr 1 \cr } } \right],x\left( t \right) = \left[ {\matrix{ {{e^{ - t}}} & { - {e^{ - 2t}}} \cr { - {e^{ - t}}} & { + 2{e^{ - 2t}}} \cr } } \right]$$ when $${x_0} = \left[ {\matrix{ 3 \cr 5 \cr } } \right],x\left( t \right)$$ is
GATE ECE 2014 Set 3
9
Consider the state space system expressed by the signal flow diagram shown in the figure.
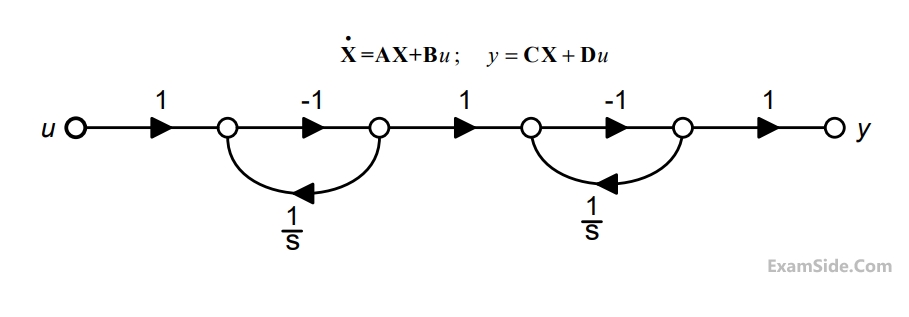
The corresponding system is
GATE ECE 2014 Set 2
10
An unforced linear time invariant (LTI) system is represented by
$$$\left[ {\matrix{
{\mathop {{x_1}}\limits^ \bullet } \cr
{\mathop {{x_2}}\limits^ \bullet } \cr
} } \right] = \left[ {\matrix{
{ - 1} & 0 \cr
0 & { - 2} \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right].$$$
If the initial conditions are x1(0)= 1 and x2(0)=-1, the solution of the state equation is
GATE ECE 2014 Set 2
11
Consider the state space model of a system, as given below
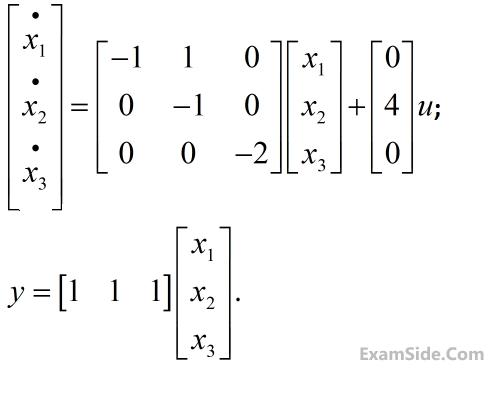
The system is
GATE ECE 2014 Set 1
12
The state diagram of a system is shown below. A system is shown below. A system is described by the state variable equations
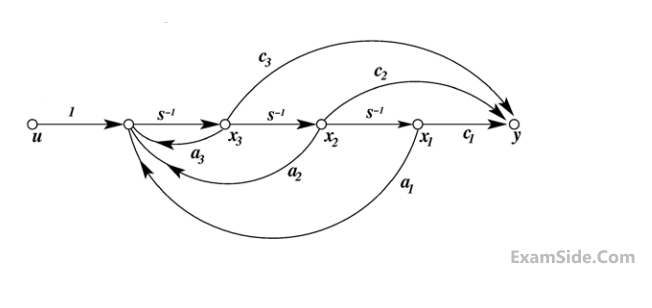
The state-variable equations of the system shown in the figure above are
GATE ECE 2013
13
The state diagram of a system is shown below. A system is shown below. A system is described by the state variable equations
The state transition matrix eAt of the system shown in the figure above is
GATE ECE 2013
14
The state variable description of an LTI system is given by
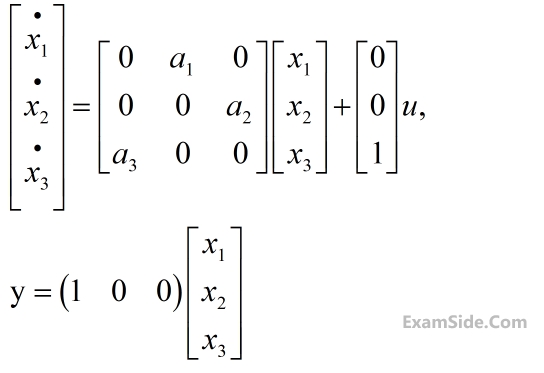
where y is the output and u is input. The system is controllable for
GATE ECE 2012
15
The block diagram of a system with one input u and two outputs y1 and y2 is given below
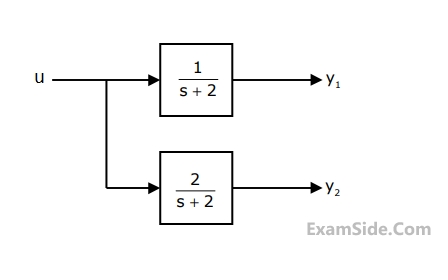
A state space model of the above system in terms of the state vector $$\underline x $$ and the output vector $$\underline y = {\left[ {\matrix{ {{y_1}} & {{y_2}} \cr } } \right]^\tau }$$ is
GATE ECE 2011
16
The signal flow graph of a system is shown below.
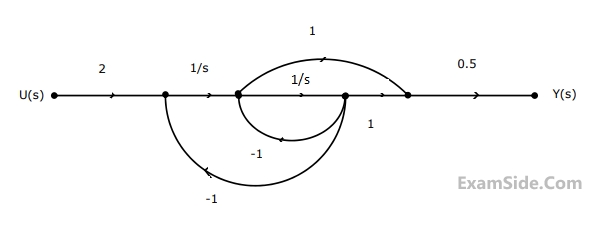
The state variable representation of the system can be
GATE ECE 2010
17
The signal flow graph of a system is shown below.
The transfer function of the system is
GATE ECE 2010
18
A signal flow graph of a system is given below.
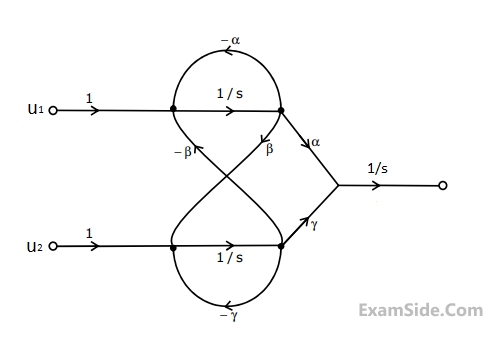
The set of equations that correspond to this signal flow graph is
GATE ECE 2008
19
Consider a linear system whose state space Representation is $$\mathop x\limits^ \bullet \left( t \right) = AX\left( t \right).$$
If the initial state vector of the system is $$x\left( 0 \right) = \left[ {\matrix{ 1 \cr { - 2} \cr } } \right],$$
then the system response is $$x\left( t \right) = \left[ {\matrix{ {{e^{ - 2t}}} \cr { - 2{e^{ - 2t}}} \cr } } \right].$$
If the initial state vector of the system changes to $$x\left( 0 \right) = \left[ {\matrix{ 1 \cr { - 1} \cr } } \right],$$
then the system response becomes $$x\left( t \right) = \left[ {\matrix{ {{e^{ - t}}} \cr { - {e^{ - t}}} \cr } } \right].$$
If the initial state vector of the system is $$x\left( 0 \right) = \left[ {\matrix{ 1 \cr { - 2} \cr } } \right],$$
then the system response is $$x\left( t \right) = \left[ {\matrix{ {{e^{ - 2t}}} \cr { - 2{e^{ - 2t}}} \cr } } \right].$$
If the initial state vector of the system changes to $$x\left( 0 \right) = \left[ {\matrix{ 1 \cr { - 1} \cr } } \right],$$
then the system response becomes $$x\left( t \right) = \left[ {\matrix{ {{e^{ - t}}} \cr { - {e^{ - t}}} \cr } } \right].$$
The eigen value and eigen vector pairs $$\left( {{\lambda _{i,}}{V_i}} \right)$$ for the system are
GATE ECE 2007
20
Consider a linear system whose state space Representation is $$\mathop x\limits^ \bullet \left( t \right) = AX\left( t \right).$$
If the initial state vector of the system is $$x\left( 0 \right) = \left[ {\matrix{ 1 \cr { - 2} \cr } } \right],$$
then the system response is $$x\left( t \right) = \left[ {\matrix{ {{e^{ - 2t}}} \cr { - 2{e^{ - 2t}}} \cr } } \right].$$
If the initial state vector of the system changes to $$x\left( 0 \right) = \left[ {\matrix{ 1 \cr { - 1} \cr } } \right],$$
then the system response becomes $$x\left( t \right) = \left[ {\matrix{ {{e^{ - t}}} \cr { - {e^{ - t}}} \cr } } \right].$$
If the initial state vector of the system is $$x\left( 0 \right) = \left[ {\matrix{ 1 \cr { - 2} \cr } } \right],$$
then the system response is $$x\left( t \right) = \left[ {\matrix{ {{e^{ - 2t}}} \cr { - 2{e^{ - 2t}}} \cr } } \right].$$
If the initial state vector of the system changes to $$x\left( 0 \right) = \left[ {\matrix{ 1 \cr { - 1} \cr } } \right],$$
then the system response becomes $$x\left( t \right) = \left[ {\matrix{ {{e^{ - t}}} \cr { - {e^{ - t}}} \cr } } \right].$$
The system matrix a is
GATE ECE 2007
21
The state space representation of a separately excited DC servo motor dynamics is given as
$$$\left[ {\matrix{
{{{d\omega } \over {dt}}} \cr
{{{d{i_a}} \over {dt}}} \cr
} } \right] = \left[ {\matrix{
{ - 1} & 1 \cr
{ - 1} & { - 10} \cr
} } \right]\left[ {\matrix{
\omega \cr
{{i_a}} \cr
} } \right] + \left[ {\matrix{
0 \cr
{10} \cr
} } \right]u.$$$
Where 'ω' is the speed of the motor, 'ia' is the armature current and u is the armature voltage. The transfer function $${{\omega \left( s \right)} \over {U\left( s \right)}}$$ of the motor is
GATE ECE 2007
22
A linear system is described by the following state equation
$$$\mathop x\limits^ \bullet \left( t \right) = AX\left( t \right) + BU\left( t \right),A = \left[ {\matrix{
0 & 1 \cr
{ - 1} & 0 \cr
} } \right].$$$
The state-transition matrix of the system is
The state-transition matrix of the system is
GATE ECE 2006
23
Given A $$ = \left[ {\matrix{
1 & 0 \cr
0 & 1 \cr
} } \right],$$ the state transition matrix eAt is given by
GATE ECE 2004
24
If A = $$\left[ {\matrix{
{ - 2} & 2 \cr
1 & { - 3} \cr
} } \right],$$ then sin At is
GATE ECE 2004
25
The state variable equations of a system are:
$$${\mathop {{x_1} = - 3{x_1} - x}\limits^ \bullet _2} + u$$$
$$${\mathop x\limits^ \bullet _2} = 2{x_1}$$$
$$$y = {x_1} + u.$$$
The system is
The system is
GATE ECE 2004
26
The zero, input response of a system given by the state space equation
$$$\left[ {{{\mathop {{x_1}}\limits^ \bullet } \over {\mathop {{x_2}}\limits^ \bullet }}} \right] = \left[ {\matrix{
1 & 0 \cr
1 & 1 \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right]and\left[ {\matrix{
{{x_1}} & {\left( 0 \right)} \cr
{{x_2}} & {\left( 0 \right)} \cr
} } \right] = \left[ {\matrix{
1 \cr
0 \cr
} } \right]is$$$
GATE ECE 2003
27
For the system described by the state
equation $$$\mathop x\limits^ \bullet = \left[ {\matrix{
0 & 1 & 0 \cr
0 & 0 & 1 \cr
{0.5} & 1 & 2 \cr
} } \right]x + \left[ {\matrix{
0 \cr
0 \cr
1 \cr
} } \right]u.$$$
If the control signal u is given by u=(-0.5-3-5)x+v, then the eigen values of the closed loop system will be
GATE ECE 1999
28
A certain linear time invariant system has the state and the output equations given below
$$$\left[ {\matrix{
{\mathop {{x_1}}\limits^ \bullet } \cr
{\mathop {{x_2}}\limits^ \bullet } \cr
} } \right] = \left[ {\matrix{
1 & { - 1} \cr
0 & 1 \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right] + \left[ {\matrix{
0 \cr
1 \cr
} } \right]u$$$
$$$y = \left[ {\matrix{
1 & 1 \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right], if$$$
$${x_1}\left( 0 \right) =1 ,{x_2}\left( 0 \right) = - 1,$$ $$u\left( 0 \right) = 0,$$ then $${{dy} \over {dt}}{|_{t = 0}}$$ is
GATE ECE 1997
29
A linear time-invariant system is described by the state variable model
$$$\left[ {\matrix{
{{{\mathop x\limits^ \bullet }_1}} \cr
{{{\mathop x\limits^ \bullet }_2}} \cr
} } \right] = \left[ {\matrix{
{ - 1} & 0 \cr
0 & { - 2} \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right] + \left[ {\matrix{
0 \cr
1 \cr
} } \right]u.$$$
$$$Y = \left[ {\matrix{
1 & 2 \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right]$$$
GATE ECE 1992
30
A linear second order single input continuous-time system is described by the
following set of differential equations
$$$\eqalign{
& \mathop {{x_1}}\limits^ \bullet \left( t \right) = - 2{x_1}\left( t \right) + 4{x_2}\left( t \right) \cr
& \mathop {{x_1}}\limits^ \bullet \left( t \right) = 2{x_1}\left( t \right) - {x_2}\left( t \right) + u\left( t \right) \cr} $$$
Where x1(t) and x2(t) are the state variables and u (t) is the control variable. The system is
Where x1(t) and x2(t) are the state variables and u (t) is the control variable. The system is
GATE ECE 1991
Marks 5
1
The block diagram of a linear time invariant system is given in Figure is
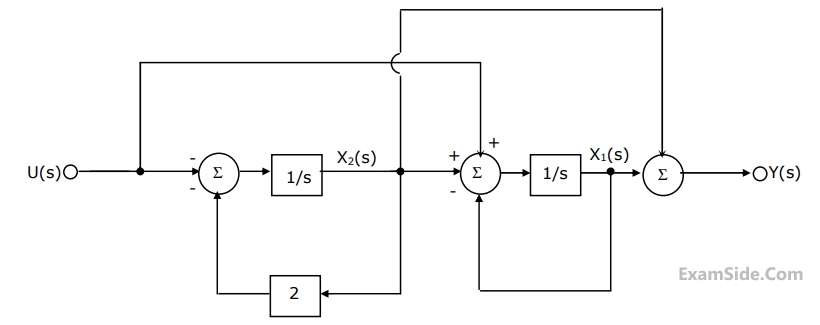(a) Write down the state variable equations for the system in matrix form
assuming the state vector to be $${\left[ {{x_1}\left( t \right)\,\,{x_2}\left( t \right)} \right]^T}$$
(b) Find out the state transition matrix.
(c) Determine y(t), t ≥ 0, when the initial values of the state at time t = 0 are $${x_1}$$(0) = 1, and $${x_2}$$(0) = 1.
(a) Write down the state variable equations for the system in matrix form
assuming the state vector to be $${\left[ {{x_1}\left( t \right)\,\,{x_2}\left( t \right)} \right]^T}$$
(b) Find out the state transition matrix.
(c) Determine y(t), t ≥ 0, when the initial values of the state at time t = 0 are $${x_1}$$(0) = 1, and $${x_2}$$(0) = 1.
GATE ECE 2002
2
A certain linear, time-invariant system has the state and output representation shown below:
$$$\eqalign{
& \left[ {\matrix{
{\mathop {{x_1}}\limits^ \bullet } \cr
{\mathop {{x_2}}\limits^ \bullet } \cr
} } \right] = \left[ {\matrix{
{ - 2} & 1 \cr
0 & { - 3} \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right] + \left[ {\matrix{
1 \cr
0 \cr
} } \right]u \cr
& y = \left( {\matrix{
1 & 1 \cr
} } \right)\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right] \cr} $$$
(a) Find the eigen values (natural frequencies) of the system.
(b)If u(t)=$$\delta \left( t \right)$$ and x1(0+)=x2(0+)=0, find x1(t),x2(t) and y(t), for t>0.
(c)When the input is zero, choose initial conditions $${x_1}\left( {{0^ + }} \right)$$ and $${x_2}\left( {{0^ + }} \right)$$ such that $$y\left( t \right) = A{e^{ - 2t}}$$ for t>0
(a) Find the eigen values (natural frequencies) of the system.
(b)If u(t)=$$\delta \left( t \right)$$ and x1(0+)=x2(0+)=0, find x1(t),x2(t) and y(t), for t>0.
(c)When the input is zero, choose initial conditions $${x_1}\left( {{0^ + }} \right)$$ and $${x_2}\left( {{0^ + }} \right)$$ such that $$y\left( t \right) = A{e^{ - 2t}}$$ for t>0
GATE ECE 2000
3
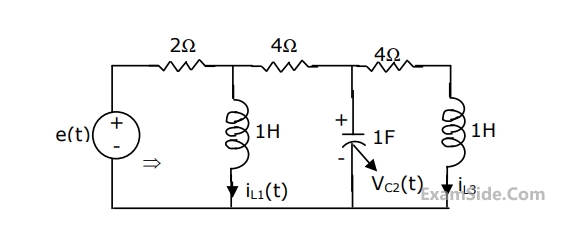
For the circuit shown in the figure, choose state variables as $${x_{1,}}{x_{2,}}{x_3}$$ to be $${i_{L1}}\left( t \right),{v_{c2}}\left( t \right),{i_{L3}}\left( t \right)$$
Wriote the state equations
$$$\left[ {\matrix{ {\mathop {{x_1}}\limits^ \bullet } \cr {\mathop {{x_2}}\limits^ \bullet } \cr {\mathop {{x_3}}\limits^ \bullet } \cr } } \right] = A\left[ {\matrix{ {{x_1}} \cr {{x_2}} \cr {{x_3}} \cr } } \right] + B\left[ {e\left( t \right)} \right]$$$GATE ECE 1997
4
Obtain a state space representation in diagonal form for the following system
$$${{{d^3}y} \over {d{t^3}}} + 6{{{d^2}y} \over {d{t^2}}} + 11{{dy} \over {dt}} + 6y = 6u\left( t \right)$$$
GATE ECE 1996
