Discrete Time Signal Z Transform · Signals and Systems · GATE ECE
Marks 1
1
Let $x[n]$ be a discrete-time signal whose $z$-transform is $X(z)$.
Which of the following statements is/are TRUE?
GATE ECE 2025
2
For a causal discrete-time LTI system with transfer function
$H(z) = \frac{2z^2 + 3}{\left(z + \frac{1}{3}\right)\left(z - \frac{1}{3}\right)}$
which of the following statements is/are true?
GATE ECE 2024
3
A discrete time all-pass system has two of its poles at
0.25$$\angle 0^\circ $$ and $$\angle 30^\circ $$. Which one of the following statements about the system is TRUE?
GATE ECE 2018
4
Consider the sequence
$$x\left[ n \right]$$= $${a^n}u\left[ n \right] + {b^{\partial n}}u\left[ n \right]$$ , where u[n] denotes the unit step sequence and 0<$$\left| a \right| < \left| b \right| < 1.$$
The region of convergence (ROC) of the z-transform of $$\left[ n \right]$$ is
$$x\left[ n \right]$$= $${a^n}u\left[ n \right] + {b^{\partial n}}u\left[ n \right]$$ , where u[n] denotes the unit step sequence and 0<$$\left| a \right| < \left| b \right| < 1.$$
The region of convergence (ROC) of the z-transform of $$\left[ n \right]$$ is
GATE ECE 2016 Set 1
5
A discrete-time signal$$x\left[ n \right]\, = \delta \left[ {n - 3} \right]\, + 2\delta \left[ {n - 5} \right]$$ has z-transform x(z). If Y (z)=X (-z) is the z-transform of another signal y$$\left[ n \right]$$, then
GATE ECE 2016 Set 3
6
Two casual discrete-time signals $$x\left[ n \right]$$ and $$y\left[ n \right]$$ =$$\sum\limits_{m = 0}^n x \left[ m \right]$$. If the z-transform of y$$\left[ n \right]$$=$${2 \over {z{{(z - 1)}^2}}}$$ , the value of $$x\left[ 2 \right]$$ is _____________________
GATE ECE 2015 Set 2
7
The sequence x $$\left[ n \right]$$ = $${0.5^n}$$ u[n], where u$$\left[ n \right]$$ is the unit step sequence, is convolved with itself to obtain y $$\left[ n \right]$$ . Then $$\sum\limits_{n = \infty }^{ + \infty } y \left[ n \right]$$ is ____________.
GATE ECE 2014 Set 4
8
For an all-pass system H(z)= $${{({z^{ - 1}} - b)} \over {(1 - a{z^{ - 1}})}}$$ where $$\left| {H({e^{ - j\omega }})} \right| = \,1$$ , for all $$\omega $$. If Re (a) $$ \ne $$ 0,$${\mathop{\rm Im}\nolimits} (a) \ne 0$$ then b equals
GATE ECE 2014 Set 3
9
An FIR system is described by the system function
$$$H(z) = 1 + {7 \over 2}{z^{ - 1}} + {3 \over 2}{z^{ - 2}}$$$
GATE ECE 2014 Set 2
10
Let x$$\left[ n \right]$$ = x$$\left[- n \right]$$ . Let X(z) be the z-transform of x$$\left[ n \right]$$. if 0.5 +j 0.25 is a zero of X(z), which one of the folowing must also be a zero of X (z)
GATE ECE 2014 Set 2
11
If $$x\left[ n \right]$$= $${(1/3)^{\left| n \right|}} - {(1/2)^n}u\left[ n \right]$$, then the region of convergence (ROC) of its Z- transform in the Z-plane will be
GATE ECE 2012
12
Consider the z-transform
X(z)=5$${z^2} + 4{z^{ - 1}} + 3;0 < \left| z \right| < \infty $$.
X(z)=5$${z^2} + 4{z^{ - 1}} + 3;0 < \left| z \right| < \infty $$.
The inverse z - transform x$$\,\left[ n \right]$$ is
GATE ECE 2010
13
The ROC of Z-transform of the discrete time sequence
x(n)= $${\left( {{1 \over 3}} \right)^{n}}u(n) - {\left( {{1 \over 2}} \right)^{ n}}\,u( - n - 1)$$ is
x(n)= $${\left( {{1 \over 3}} \right)^{n}}u(n) - {\left( {{1 \over 2}} \right)^{ n}}\,u( - n - 1)$$ is
GATE ECE 2009
14
If the region of convergence of $${x_1}\left[ n \right]$$ + $${x_2}\left[ n \right]$$ is 1/3< $$\left| {z\,} \right|$$<2/3, then the region of convergence of $${x_1}\left[ n \right]$$ - $${x_2}\left[ n \right]$$ includes
GATE ECE 2006
15
The region of convergence of z-transform of the sequence $${\left( {{5 \over 6}} \right)^n}u(n) - {\left( {{6 \over 5}} \right)^n}u( - n - 1)$$ must be
GATE ECE 2005
16
The z transform of a system is
H(z) = $${z \over {z - 0.2}}$$ .
If the ROC is $$\left| {z\,} \right|$$ < 0.2, then the impulse response of the system is
H(z) = $${z \over {z - 0.2}}$$ .
If the ROC is $$\left| {z\,} \right|$$ < 0.2, then the impulse response of the system is
GATE ECE 2004
17
The region of convergence of the z- transform of a unit step function is
GATE ECE 2001
18
The z-transform F(z) of the function f(nT) = $${a^{nT}}$$ is
GATE ECE 1999
19
The z - transform of the time function $$\sum\limits_{k = 0}^\infty {\delta \left( {n - k} \right)} $$ is
GATE ECE 1998
Marks 2
1
A sequence x$$\left[ n \right]$$ is specified as $$\left[ {\matrix{
{x\left[ n \right]} \cr
{x\left[ {n - 1} \right]} \cr
} } \right] = {\left[ {\matrix{
1 \cr
1 \cr
} \,\matrix{
1 \cr
0 \cr
} } \right]^n}\left[ {\matrix{
1 \cr
0 \cr
} } \right]$$, for n $$ \ge $$2.
The initial conditions are x$$\left[ 0 \right]$$ = 1, x$$\left[ 1 \right]$$=1 and x$$\left[ n \right]$$=0 for n< 0. The value of x$$\left[ 12 \right]$$ is _____________________.
The initial conditions are x$$\left[ 0 \right]$$ = 1, x$$\left[ 1 \right]$$=1 and x$$\left[ n \right]$$=0 for n< 0. The value of x$$\left[ 12 \right]$$ is _____________________.
GATE ECE 2016 Set 1
2
The ROC (region of convergence) of the z-transform of a discrete-time signal is represented by the shaded
region in the z-plane. If the signal $$x\left[ n \right] = \,{\left( {2.0} \right)^{\left| n \right|}}$$ , $$ - \infty < n < + \infty $$ then the ROC of its z-transform is
represented by
GATE ECE 2016 Set 3
3
For the discrete-time system shown in the figure, the poles of the system transfer function are located at
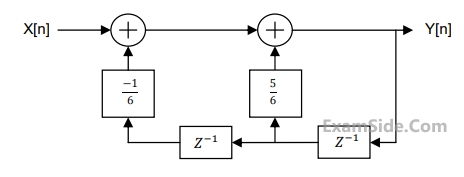

GATE ECE 2015 Set 1
4
The pole-zero diagram of a causal and stable discrete-time system is shown in the figure. The zero at the origin has
multiplicity 4. The impulse response of the system is ℎ[n]. If ℎ[0] =1, we can conclude.


GATE ECE 2015 Set 1
5
Suppose x $$\left[ n \right]$$ is an absolutely summable discrete-time signal. Its z-transform is a rational function
with two poles and two zeroes. The poles are at z = ± 2j. Which one of the following statements is
TRUE for the signal x=$$\left[ n \right]$$ ?
GATE ECE 2015 Set 3
6
A realization of a stable discrete time system is shown in the figure. If the system is excited by a
unit step sequence input x[n ] , the response y[ n] is


GATE ECE 2015 Set 3
7
Let $${H_1}(z) = {(1 - p{z^{ - 1}})^{ - 1}},{H_2}(z) = {(1 - q{z^{^{ - 1}}})^{ - 1}}$$ , H(z) =$${H_1}(z)$$ +r $${H_2}$$. The quantities p, q, r are real numbers. Consider , p=$${1 \over 2}$$, q=-$${1 \over 4}$$ $$\left| r \right|$$ <1. If the zero H(z) lies on the unit circle, the r = ____________________________.
GATE ECE 2014 Set 3
8
The z-transform of the sequence x$$\left[ n \right]$$ is given by x(z)= $${1 \over {{{(1 - 2{z^{ - 1}})}^2}}}$$ , with the region of convergence $$\left| z \right| > 2$$. Then, $$x\left[ 2 \right]$$ is ____________________.
GATE ECE 2014 Set 3
9
The input-output relationship of a causal stable LTI system is given as
𝑦[𝑛] = 𝛼 𝑦[𝑛 − 1] + $$\beta $$ x[n].
If the impulse response h[n] of this system satisfies the condition $$\sum\limits_{n = 0}^\infty h $$[n] = 2, the relationship between α and is $$\alpha $$ and $$\beta $$ is
𝑦[𝑛] = 𝛼 𝑦[𝑛 − 1] + $$\beta $$ x[n].
If the impulse response h[n] of this system satisfies the condition $$\sum\limits_{n = 0}^\infty h $$[n] = 2, the relationship between α and is $$\alpha $$ and $$\beta $$ is
GATE ECE 2014 Set 2
10
Let x $$\left[ n\right]$$= $${\left( { - {1 \over 9}} \right)^n}\,u(n) - {\left( { - {1 \over 3}} \right)^n}u( - n - 1).$$ The region of Convergence (ROC) of the z-tansform of x$$\left[ n \right]$$
GATE ECE 2014 Set 1
11
In the following network (Fig.1), the switch is closed at t = 0 and the sampling starts from t=0. The sampling frequency is 10 Hz.
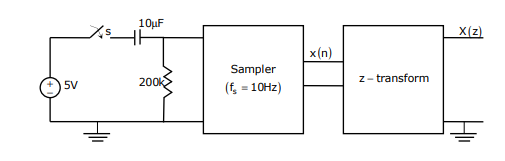

The samples x (n) (n=0, 1, 2,...........) are given by
GATE ECE 2008
12
In the following network (Fig .1), the switch is closed at t = 0- and the sampling starts from t = 0. The sampling frequency is 10 Hz.
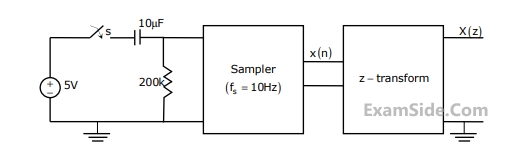
The expression and the region of convergence of the z-transform of the sampled signal are

The expression and the region of convergence of the z-transform of the sampled signal are
GATE ECE 2008
13
The z-transform X (z) f a sequence x$$\left[ n \right]$$ is given by = $${{0.5} \over {1 - 2{z^{ - 1}}}}$$ . It is given that the region of convergence of X$$\left[ z \right]$$ includes the unit circle. The value of x$$\left[ 0 \right]$$ is
GATE ECE 2007
14
The z-transform of a signal is given by c(z)=$${1 \over 4}{{{z^{ - 1}}(1 - {z^{ - 4}})} \over {{{(1 - {z^{ - 1}})}^2}}}$$. Its final value is
GATE ECE 1999
15
The Z-transform of the following real exponential sequence:
x(nT) = $${a^n}$$, nT $$ \ge $$ 0
=0, nT<0, a> 0
gives us by
x(nT) = $${a^n}$$, nT $$ \ge $$ 0
=0, nT<0, a> 0
gives us by
GATE ECE 1990