Transmission of Signal Through Continuous Time LTI Systems · Signals and Systems · GATE ECE
Marks 1
Let x1(t) = e$$-$$t u(t) and x2(t) = u(t) $$-$$ u(t $$-$$ 2), where u( . ) denotes the unit step function. If y(t) denotes the convolution of x1(t) and x2(t), then $$\mathop {\lim }\limits_{t \to \infty } y(t)$$ = __________ (rounded off to one decimal place).
$$H(f) = \left\{ {\matrix{ {{e^{ - j4\pi f}},} & {\left| f \right| \le \,{W \over 2}} \cr {0,} & {\left| f \right| > \,{W \over 2}} \cr } } \right.$$
The output of the system is
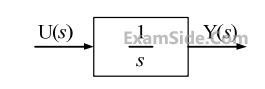
$$y(t) = \cos \left( {2t - {\pi \over 3}} \right)\,$$ for the input signal
$$x(t) = p\cos \left( {2t - {\pi \over 2}} \right)$$. Then, the system parameter 'p' is
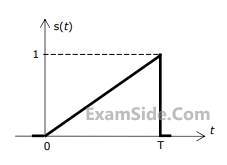
x(t) = (sint)u(t). In steady-state, the response y(t) will be
Marks 2
Let $$x(t) = 100\cos (10.5Wt)$$ be passed through an LTI system having impulse response $$h(t) = \pi {\left( {{{\sin Wt} \over {\pi t}}} \right)^2}\cos 10Wt$$. The output of the system is
The outputs of four systems (S1, S2, S3 and S4) corresponding to the input signal sin(t), for all time t, are shown in the figure.
Based on the given information, which of the four systems is/are definitely NOT LTI (linear and time-invariant)?

X: Impulse P: 1 $$ - {e^{ - t/T}}$$
Y: Unit step Q: t $$ - T(1 - {e^{ - t/T}})$$
Z: Ramp R: $${e^{ - t/T}}$$


Let H(t) denote the frequency response of the RC-LPF. Let $${f_1}$$ be the highest frequency such that $$0 \le \left| f \right| \le {f_1},{{\left| {H({f_1})} \right|} \over {H(0)}} \ge 0.95$$. Then $${f_1}$$ (in Hz) is
Let $${t_g}$$ (f) be the group delay function of the given RC-LPF and $${f_2}$$ = 100 Hz. Then $${t_g}$$$${(f_2)}$$ in ms, is
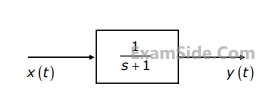
The output y(t) will be
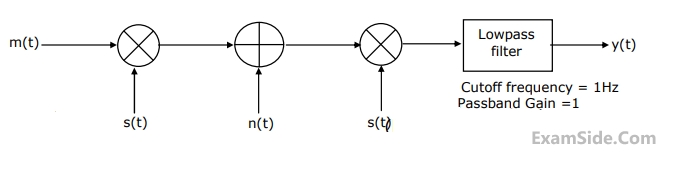
The peak amplitude of the filter output is

H(s) = $${{K({s^2} + {\omega _0}^2)} \over {{s^2} + ({\omega _0}/Q)s + {\omega _0}^2}}$$
Marks 5

Calculate the value of the ratio, $${a \over b}$$, for which 50% of the input signal energy is transferred to the output.
