Random Signals and Noise · Communications · GATE ECE

A white Gaussian noise $w(t)$ with zero mean and power spectral density $\frac{N_0}{2}$,

when applied to a first-order RC low pass filter produces an output $n(t)$. At a particular time $t = t_k$, the variance of the random variable $n(t_k)$ is ________.

For a real signal, which of the following is/are valid power spectral density/densities?

The frequency response H(f) of a linear time-invariant system has magnitude as shown in the figure.

Statement I : The system is necessarily a pure delay system for inputs which are bandlimited to $$-$$$$\alpha$$ $$\le$$ f $$\le$$ $$\alpha$$.

Statement II : For any wide-sense stationary input process with power spectral density S_X(f), the output power spectral density S_Y(f) obeys S_Y(f) = S_X(f) for $$-$$$$\alpha$$ $$\le$$ f $$\le$$ $$\alpha$$.

Which one of the following combinations is true?

The probability of the event {X = 4} is

The value of K should be

A source transmits a symbol $s$, taken from $\\{-4, 0, 4\\}$ with equal probability, over an additive white Gaussian noise channel. The received noisy symbol $r$ is given by $r = s + w$, where the noise $w$ is zero mean with variance 4 and is independent of $s$.

Using $Q(x) = \frac{1}{\sqrt{2\pi}} \int\limits_{x}^{\infty} e^{-\frac{t^{2}}{2}} dt$, the optimum symbol error probability is _______.

Let $X(t) = A\cos(2\pi f_0 t+\theta)$ be a random process, where amplitude $A$ and phase $\theta$ are independent of each other, and are uniformly distributed in the intervals $[-2,2]$ and $[0, 2\pi]$, respectively. $X(t)$ is fed to an 8-bit uniform mid-rise type quantizer.

Given that the autocorrelation of $X(t)$ is $R_X(\tau) = \frac{2}{3} \cos(2\pi f_0 \tau)$, the signal to quantization noise ratio (in dB, rounded off to two decimal places) at the output of the quantizer is _________.

A random variable X, distributed normally as N(0, 1), undergoes the transformation Y = h(X), given in the figure. The form of the probability density function of Y is

(In the options given below, a, b, c are non-zero constants and g(y) is piece-wise continuous function)

Let X(t) be a white Gaussian noise with power spectral density $$\frac{1}{2}$$W/Hz. If X(t) is input to an LTI system with impulse response $$e^{-t}u(t)$$. The average power of the system output is ____________ W (rounded off to two decimal places).

Consider a real valued source whose samples are independent and identically distributed random variables with the probability density function, f(x), as shown in the figure.

Consider a 1 bit quantizer that maps positive samples to value $$\alpha$$ and others to value $$\beta$$. If $$\alpha$$* and $$\beta$$* are the respective choices for $$\alpha$$ and $$\beta$$ that minimize the mean square quantization error, then ($$\alpha$$* $$-$$ $$\beta$$*) = ___________ (rounded off to two decimal places).

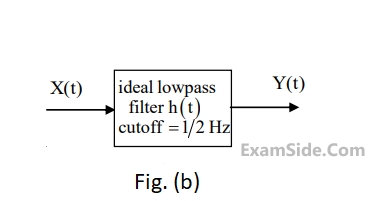
As shown in Figure (b). The output of the low pass filter is $$y(t)$$.

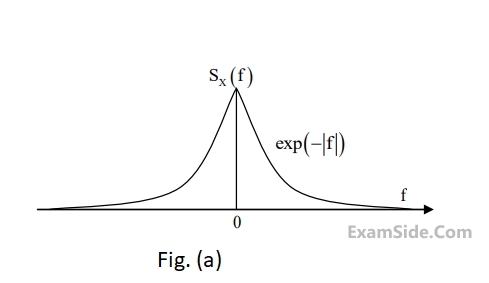
Let $$E$$ be the expectation operator and consider the following statements :
$$\left( {\rm I} \right)$$ $$E\left( {X\left( t \right)} \right) = E\left( {Y\left( t \right)} \right)$$
$$\left( {{\rm I}{\rm I}} \right)$$ $$\,\,\,\,\,\,\,\,E\left( {{X^2}\left( t \right)} \right) = E\left( {{Y^2}\left( t \right)} \right)$$
$$\left( {{\rm I}{\rm I}{\rm I}} \right)\,$$ $$\,\,\,\,\,\,E\left( {{Y^2}\left( t \right)} \right) = 2$$

Select the correct option:

$$x\left( t \right) = \sum\limits_{n = - \infty }^\infty {{\beta _n}g\left( {t - nT} \right),} $$ where $$g\left( t \right) = \left\{ {\matrix{ {1,} & {0 \le t \le T} \cr 0 & {otherwise} \cr } } \right.$$

If there is a null at $$f = {1 \over {3T}}$$ in the power spectral density of $$X(t)$$, then $$k$$ is _________.

If $$P\left( {X\,\, = 0} \right)\,\, = p$$ and $$P\left( {Y\,\, = 0} \right)\,\, = q,$$ then $$P\left( {X + Y \ge 1} \right)$$ is equal to

where $$p(t) = u(t) - u(t - T)$$, $$u(t)$$ is the unit step function and $$\phi $$ is an independent random variable with uniform distribution in $$[0, T]$$. The sequence $$\left\{ {{X_n}} \right\}$$ consists of independent and identically distributed binary valued random variables with $$P\left\{ {{X_n} = + 1} \right\} = P\left\{ {{X_n} = - 1} \right\} = 0.5$$ for each $$n$$.

The value of the autocorrelation $${R_{yy}}\left( {{{3T} \over 4}} \right)\underline{\underline \Delta } E\left[ {y\left( t \right)y\left( {t - {{3T} \over 4}} \right)} \right]\,\,$$

Where f is the frequency expressed in $$Hz$$. The signal $$X( t )$$ modulates a carrier cos $$16000$$ $$\pi t$$ and the resultant signal is passed through an ideal band-pass filter of unity gain with centre frequency of $$8kHz$$ and band-width of $$2kHz$$. The output power (in Watts) is ______.

The value of the expectation $$$E\left[ {\pi X\left( t \right)X\left( {t - {1 \over {4W}}} \right)} \right]$$$
is ---------------.

If the BER of this system is $$Q\left( {b\sqrt y } \right),$$ then the value of b is -----------.

If the detection threshold is 1, the BER will be

The optimum threshold to achieve minimum bit error rate (BER) is

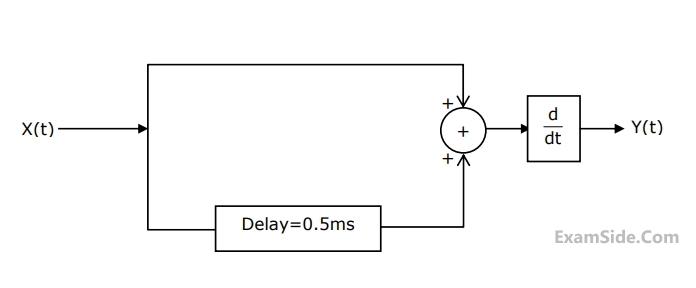
Let S_y(f) be the power spectral density of Y(t). Which one of the following statements is correct?

It is desired to generate a stochastic process (as voltage process) with power spectral density

By driving a Linear-Time-Invariant system by zero mean white noise (as voltage process) with power spectral density being constant equal to 1. The system which can perform the desired task could be

The parameters of the system obtained in Q. 12 would be