Discrete Time Linear Time Invariant Systems · Signals and Systems · GATE ECE
Marks 1
For a causal discrete-time LTI system with transfer function
$H(z) = \frac{2z^2 + 3}{\left(z + \frac{1}{3}\right)\left(z - \frac{1}{3}\right)}$
which of the following statements is/are true?
Consider a system with input $$x(t)$$ and output $$y(t) = x({e^t})$$. The system is
$$y\left[ n \right]\, = \left\{ {\matrix{ {n\left| {x\left[ n \right]} \right|,} & {for\,\,0 \le n \le 10} \cr {x\left[ n \right] - x\left[ {n - 1} \right],} & {otherwise,} \cr } } \right.$$
Which one of the following statements is true about the system?
$$h\left( n \right) = 5\delta \left[ n \right] - 7\delta \left[ {n - 1} \right] + 7\delta \left[ {n - 3} \right] - 5\delta \left[ {n - 4} \right]$$ is a
where $$\matrix{ {\delta \left( n \right) = 1,} & {n = 0} \cr {0,} & {otherwise} \cr } $$
The output at $$n = 4$$ is
Marks 2
Suppose $${x_1}\left[ n \right]$$ $$ = \alpha \,{0.5^n}\,u\left[ n \right],$$ where $$\alpha $$ is a positive real number and $$u\left[ n \right]\,$$ is the unit step sequence. Assume $$${x_2}\left[ n \right] = \,\left\{ {\matrix{ {\sqrt {1.5} } & {for\,\,\,n = 0,1} \cr 0 & {otherwise} \cr } } \right.$$$
Then the value of $$\,\alpha $$ is________.
$$x\left[ n \right] = \left\{ {\matrix{ {n\,\,for\,\,0 \le n \le 10} \cr {0\,\,otherwise} \cr } } \right.$$
If $$y\left[ n \right]$$ is the convolution of $$x\left[ n \right]$$ with itself, the value of $$y\left[ 4 \right]$$ is
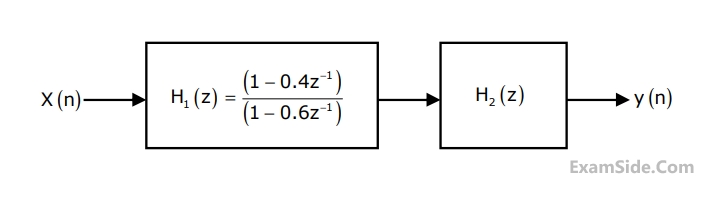
$$H\left( z \right) = {{2 - {3 \over 4}{z^{ - 1}}} \over {1 - {3 \over 4}{z^{ - 1}} + {1 \over 8}{z^{ - 2}}}}$$
Consider the following statements:
S1: The system is stable and causal for $$ROC:\,\,\,\left| z \right| > \,1/2$$
S2: The system is stable but not causal for $$ROC:\,\,\,\left| z \right| < \,1/4$$
S3: The system is neither stable nor causal for $$ROC:\,\,1/4\, < \,\left| z \right| < \,{\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}$$
Which one of the following statements is valid?
$$h\left[ n \right] = \left\{ {\matrix{ { - 2\sqrt 2 ,} & {n = 1, - 1} \cr {4\sqrt 2 ,} & {n = 2, - 2} \cr {0,} & {otherwise} \cr } } \right.$$
If the input to the above system is the sequence $${e^{j\pi n/4}},$$ then the output is
A discrete time system has the input-output relationship,
$$y\left( n \right) = \left\{ {\matrix{ {x\left( n \right),} & {n \ge 1} \cr {0,} & {n = 0} \cr {x\left( {n + 1} \right),} & {n \le - 1} \cr } } \right.$$
Where $$x\left( n \right)\,$$ is the input and $$y\left( n \right)\,$$ is the output. The above system has the properties
Marks 4
Marks 5
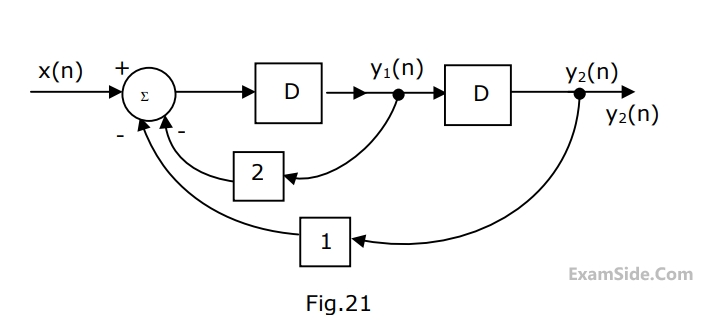
(a) Find the expression for $${y_1}\left( n \right)$$ and $${y_2}\left( n \right)$$ in terms of $$x\left( n \right).$$
(b) Find the transfer function $${y_2}\left( z \right)/X\left( z \right)$$ in the $$z$$-domain.
(c) If $$x\left( n \right) = 1$$ at $$n = 0$$ or $$x\left( n \right) = 0$$ otherwise
Find $${y_2}\left( n \right).$$
