Time Response Analysis · Control Systems · GATE ECE
Marks 1
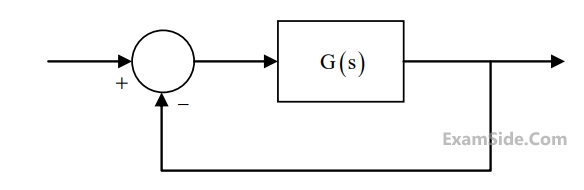
In the feedback control system shown in the figure below $G(s) = \dfrac{6}{s(s+1)(s+2)}$.

$R(s), Y(s),$ and $E(s)$ are the Laplace transforms of $r(t), y(t),$ and $e(t)$, respectively. If the input $r(t)$ is a unit step function, then __________
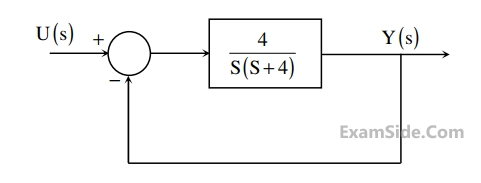
 Given that the steady state error is zero for unit step input and is 6 for unit ramp input, the
value of the parameter p is _________.
Given that the steady state error is zero for unit step input and is 6 for unit ramp input, the
value of the parameter p is _________.

Marks 2
Consider a unity negative feedback control system with forward path gain $G(s) = \frac{K}{(s + 1)(s + 2)(s + 3)}$ as shown.

The impulse response of the closed-loop system decays faster than $e^{-t}$ if ________.
A closed loop system is shown in the figure where $$k>0$$ and $$\alpha > 0$$. The steady state error due to a ramp input $$(R(s) = \alpha /{s^2})$$ is given by

Two linear time-invariant systems with transfer functions
$${G_1}(s) = {{10} \over {{s^2} + s + 1}}$$ and $${G_2}(s) = {{10} \over {{s^2} + s\sqrt {10} + 10}}$$
have unit step responses y1(t) and y2(t), respectively. Which of the following statements is/are true?
The block diagram of a closed-loop control system is shown in the figure. R(s), Y(s), and D(s) are the Laplace transforms of the time-domain signals r(t), y(t), and d(t), respectively. Let the error signal be defined as e(t) = r(t) $$-$$ y(t). Assuming the reference input r(t) = 0 for all t, the steady-state error e($$\infty$$), due to a unit step disturbance d(t), is __________ (rounded off to two decimal places).

 The required value of gain k to achieve this is __________.
The required value of gain k to achieve this is __________.
 Which one of the following compensators C(s) achieves this?
Which one of the following compensators C(s) achieves this?

Group I $$$P=\frac{25}{s^2+25}\;\;\;\;\;Q=\frac{36}{s^2+20s+36}$$$ $$$R=\frac{36}{s^2+12s+36}\;\;\;\;\;S=\frac{49}{s^2+7s+49}$$$
Group II




List-1
(a) Very low response at very high frequencies.
(b) Overshoot
(c) Synchro-control transformer output
List-2
(1) Low pass systems
(2) Velocity damping
(3) Natural frequency
(4) Phase-sensitive modulation
(5) Damping ration
(a) Over damped
(b) Critically damped
(c) Oscillatory
If the transfer function has
(1) poles on the negative real axis
(2) poles on the imaginary axis
(3) multiple poles on the positive real axis
(4) poles on the positive real axis
(5) multiple poles on the negative real axis
Marks 5
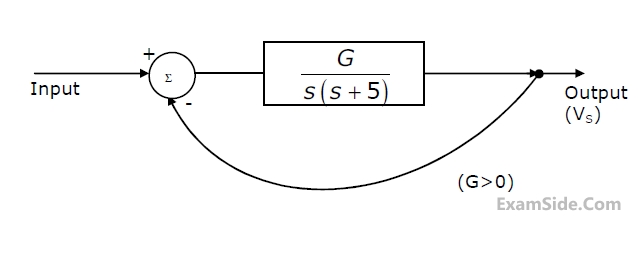
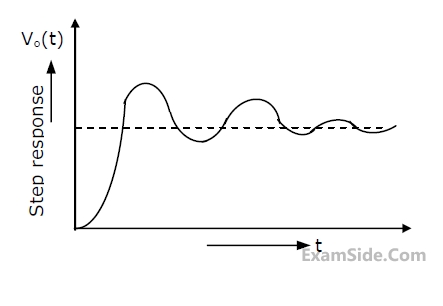
(a) Find the closed loop transfer function.
(b) Find the minimum value of G for which the step response of the system would exhibit an overshoot, as shown in Figure.
(c) For G equal to twice this minimum value, find the time period T indicated in Figure.
 (a) Find the transfer function $$\frac{y\left(s\right)}{x\left(s\right)}$$
when k =1.
(a) Find the transfer function $$\frac{y\left(s\right)}{x\left(s\right)}$$
when k =1.
(b) Find the impulse response when k = 0.
(c) Find the values of k for which the system becomes unstable.
Marks 8
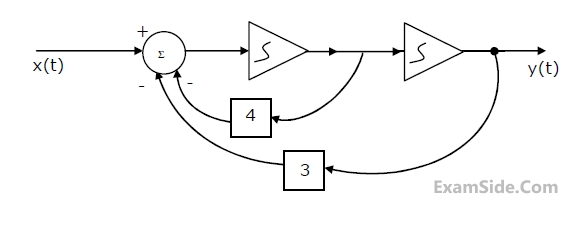
(a) Find the transfer function.
(b) For the step response of the system [i.e. find y(t) when x(t) is a unit step function and the initial conditions are zero]
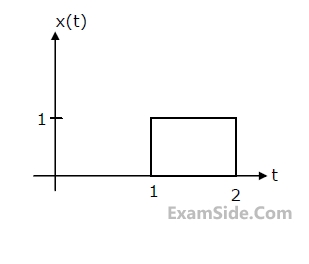
(c) Find y(t), if x(t) is as shown in Fig. and the initial conditions are zero.

(a) In absence of derivative feedback (Kt=0) , determine damping ratio of the system for amplifier gain KA=5. Also find the steady state error to unit ramp input.
(b) Find suitable values of the parameters KA and Kt so that damping ratio of the system is increased to 0.7 without affecting the steady state error as obtained in part (a).
