Sampling · Signals and Systems · GATE ECE
Marks 1
where $$x\left( t \right) = 10\,\,\cos \,\left( {8\pi \times {{10}^3}} \right)\,\,t$$ and
$${T_s} = 100\,\,\mu \sec .$$ When $$y\left( t \right)$$ is passed through an ideal low-pass filter with a cutoff frequency of 5 KHz, the output of the filter is

Marks 2
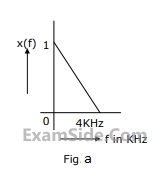
Consider a continuous-time finite-energy signal $f(t)$ whose Fourier transform vanishes outside the frequency interval $\left[-\omega_c, \omega_c\right]$, where $\omega_c$ is in rad/sec.
The signal $f(t)$ is uniformly sampled to obtain $y(t)=f(t) p(t)$. Here
$$ p(t)=\sum_{n=-\infty}^{\infty} \delta\left(t-\tau-n T_s\right) $$
with $\delta(t)$ being the Dirac impulse, $T_s>0$, and $\tau>0$. The sampled signal $y(t)$ is passed through an ideal lowpass filter $h(t)=\omega_c T_s \frac{\sin \left(\omega_c t\right)}{\pi \omega_c t}$ with cutoff frequency $\omega_c$ and passband gain $T_s$.
The output of the filter is given by $\qquad$ .
A continuous time signal $x(t) = 2 \cos(8 \pi t + \frac{\pi}{3})$ is sampled at a rate of 15 Hz. The sampled signal $x_s(t)$ when passed through an LTI system with impulse response
$h(t) = \left( \frac{\sin 2 \pi t}{\pi t} \right) \cos(38 \pi t - \frac{\pi}{2})$
produces an output $x_o(t)$. The expression for $x_o(t)$ is ______.
What is the number of sinusoids in the output and their frequency inkHz?
would be
The resulting signal is then passed through an ideal low pass filter with bandwidth 1 kHz. The output of the low pass filter would be
Marks 4
Marks 5
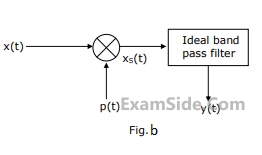
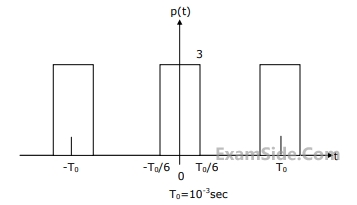
(a) Calculate the Fourier series coefficients $${c_n}$$ in the Fourier expansion of p(t) in form $$p(t) = \sum\limits_{n = - \infty }^{ + \infty } {{c_n}} \,\exp \,\,(j\,n\,2\pi \,t/T)$$.
(b) Find the Fourier Transform of p(t).
(c) Obtain and sketch the spectrum of $${x_s}(t)$$.
(d) Obtain and sketch the spectrum of y(t).