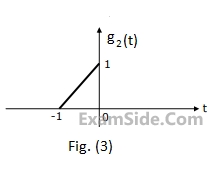Fourier Transform · Signals and Systems · GATE ECE
Marks 1
1
Let $$m(t)$$ be a strictly band-limited signal with bandwidth B and energy E. Assuming $${\omega _0} = 10B$$, the energy in the signal $$m(t)\cos {\omega _0}t$$ is
GATE ECE 2023
2
The Fourier transform $$x(\omega )$$ of $$x(t) = {e^{ - {t^2}}}$$ is
Note : $$\int\limits_{ - \infty }^\infty {{e^{ - {y^2}}}dy = \sqrt \pi } $$
GATE ECE 2023
3
Which one of the following is an eight function of the class of all continuous-time, linear, time- invariant systems u(t) denotes the unit-step function?
GATE ECE 2016 Set 1
4
If the signal x(t) = $${{\sin (t)} \over {\pi t}}*{{\sin (t)} \over {\pi t}}$$ with * denoting the convolution operation, then x(t) is equal to
GATE ECE 2016 Set 3
5
The energy of the signal x(t) =$${{\sin (4\pi t)} \over {4\pi t}}$$ is ___________.
GATE ECE 2016 Set 2
6
Let x(t) $$ \leftrightarrow $$ X($$(j\omega )$$ BE Fourier transform pair. The Fourier Transform of the signal x(5t - 3) in terms of X($$(j\omega )$$ is given as
GATE ECE 2006
7
The Fourier transform of a conjugate symmetric function is always
GATE ECE 2004
8
The Fourier transform F $$\left\{ {{e^{ - t}}u(t)} \right\}$$ is equal to $${1 \over {1 + j2\pi f}}$$. Therefore, $$F\left\{ {{1 \over {1 + j2\pi t}}} \right\}$$ is
GATE ECE 2002
9
If a signal f(t) has energy E, the energy of the signal f(2t) is equal to
GATE ECE 2001
10
The Fourier Transform of the signal $$x(t) = {e^{ - 3{t^2}}}$$ is of the following form, where A
and B are constants:
GATE ECE 2000
11
A signal x(t) has a Fourier transform X ($$\omega $$). If x(t) is a real and odd function of t, then X($$\omega $$) is
GATE ECE 1999
12
A modulated signal is given by s(t)= $${e^{ - at}}$$ cos $$\left[ {({\omega _c} + \Delta \omega )t} \right]$$ u (t), where a, $${\omega _c}$$ and $${\Delta \omega }$$ are positive constants, and $${\omega _c}$$ >>$${\Delta \omega }$$. The complex envelope of s(t) is given by
GATE ECE 1999
13
The Fourier transform of a function x(t) is X(f). The Fourier transform of $${{dx(t)} \over {dt}}$$ will be
GATE ECE 1998
14
The Fourier transform of a voltage of a voltage signal x(t) is X(f). The unit of |X(f)| is
GATE ECE 1998
15
The amplitude spectrum of a Gaussian pulse is
GATE ECE 1998
16
The function f(t) has the Fourier Transform g($$\omega $$). The Fourier Transform of $$$g(t) = \left( {\int\limits_{ - \infty }^\infty {g(t){e^{ - j\omega t}}} } \right)\,is$$$
GATE ECE 1997
17
The Fourier transform of a real valued time signal has
GATE ECE 1996
Marks 2
1
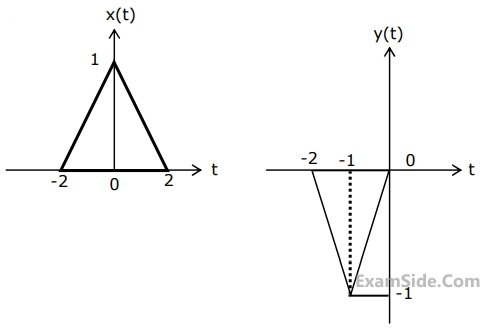
Consider two continuous time signals $x(t)$ and $y(t)$ as shown below
If $X(f)$ denotes the Fourier transform of $x(t)$, then the Fourier transform of $y(t)$ is ______.
GATE ECE 2024
2
The complex envelope of the bandpass signal $$x(t)\, = \, - \sqrt 2 \left( {{{\sin (\pi t/5)} \over {\pi t/5}}} \right)\sin \left( {\pi t - {\pi \over 4}} \right),$$ centered about f = $${1 \over {2\,}}\,Hz,$$ is
GATE ECE 2015 Set 3
3
The value of the integral $$\int_{ - \infty }^\infty {12\,\cos (2\pi )\,{{\sin (4\pi t)} \over {4\pi t}}\,dt\,} $$ is
GATE ECE 2015 Set 2
4
For a function g(t), it is given that $$\int_{ - \infty }^\infty {g(t){e^{ - j\omega t}}dt = \omega {e^{ - 2{\omega ^2}}}} $$ for any real value $$\omega $$. If y(t)=$$\int_{ - \infty }^t {g(\tau )d\tau ,\,then\,\int_{ - \infty }^\infty {y(t)\,dt} \,} $$ is
GATE ECE 2014 Set 1
5
The value of the integral $$\int\limits_{ - \infty }^\infty {\sin \,{c^2}} $$ (5t) dt is
GATE ECE 2014 Set 2
6
The Fourier transform of a signal h(t) is $$H(j\omega )$$ =(2 cos $$\omega $$) (sin 2$$\omega $$) / $$\omega $$. The value of h(0) is
GATE ECE 2012
7
The signal x(t) is described by $$x\left( t \right) = \left\{ {\matrix{
{1\,\,\,for\,\, - 1 \le t \le + 1} \cr
{0\,\,\,\,\,\,\,\,\,\,\,\,\,\,otherwise} \cr
} } \right.$$
Two of the angular frequencies at which its Fourier transform becomes zero are
GATE ECE 2008
8
For a signal x(t) the Fourier transform is X(f). Then the inverse Fourier transform of X(3f+2) is given by
GATE ECE 2005
9
Let x(t) and y(t) (with Fourier transforms X(f) and Y(f) respectively) be related as shown in Fig.(1) & (2).
Then Y(f) is
GATE ECE 2004
10
The Hilbert transform of $$\left[ {\cos \,{\omega _1}t + \,\sin {\omega _2}t\,} \right]$$ is
GATE ECE 2000
11
If the Fourier Transfrom of a deterministic signal g(t) is G (f), then
Match each of the items 1, 2 on the left with the most appropriate item A, B, C or D on the right.
Item-1
(1) The Fourier transform of g (t - 2) is
(2) The Fourier transform of g (t/2) is
Item - 2
(A) G(f) $$e^{-j\left(4\mathrm{πf}\right)}$$
(B) G(2f)
(C) 2G(2f)
(D) G(f-2)
Match each of the items 1, 2 on the left with the most appropriate item A, B, C or D on the right.
GATE ECE 1997
12
The power spectral density of a deterministic signal is given by $${\left[ {\sin (f)/f} \right]^2}$$, where 'f' is frequency. The autocorrelation function of this signal in the time domain is
GATE ECE 1997
13
The autocorrelation function of an energy signal has
GATE ECE 1996
14
If G(f) represents the Fourier transform of a signal g (t) which is real and odd symmetric in time, then
GATE ECE 1992
Marks 5
1
The Fourier transform $$G(\omega )$$ of the signal g(t) in Fig.(1) is given as
$$G(\omega ) = {1 \over {{\omega ^2}}}({e^{j\omega }} - j\omega {e^{j\omega }} - 1)$$.
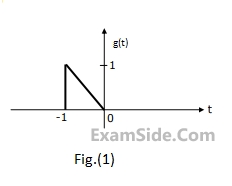
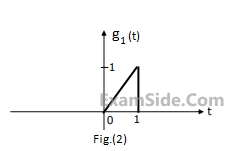
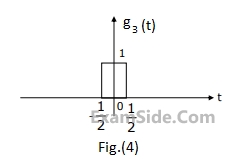
$$G(\omega ) = {1 \over {{\omega ^2}}}({e^{j\omega }} - j\omega {e^{j\omega }} - 1)$$.
Using this information, and the time-shifting and time-scaling properties, determine and Fourier transform of signals in Fig (2), (3) and (4).
GATE ECE 2001
2
Consider a rectangular pulse g(t) existing between $$t = \, - {T \over 2}\,and\,{T \over 2}$$. Find and sketch the pulse obtained by convolving g(t) with itself. The Fourier transform of g(t) is a sinc function. Write down the Fourier transform of the pulse obtained by the above convolution.
GATE ECE 1998
3
A signal v(t)= [1+ m(t) ] cos $$({\omega _c}t)$$ is detected using a square law detector, having the characteristic $${v_0}(t) = {v^2}(t)$$. If the Fourier transform of m(t) is constant, $${M_0}$$, extending from - $${f_{m\,}}\,to\, + {f_{m\,}}$$, sketch the Fourier transform of $${v_0}(t)$$ in the frequency range-$${f_{m\,}}\, < f < {f_{m\,}}$$.
GATE ECE 1995