Boolean Algebra · Digital Circuits · GATE ECE
Marks 1
For the Boolean function
$F(A, B, C, D) = \sum m(0,2,5,7,8,10,12,13,14,15)$,
the essential prime implicants are _________.
Select the Boolean function(s) equivalent to x + yz, where x, y, and z are Boolean variables, and + denotes logical OR operation.
F = $$\overline A .\overline B .\overline C + \overline A .B.\overline C + A.\overline B .\overline C $$
where, $$\overline A $$, $$\overline B $$, and $$\overline C $$ are the complements of the respective variables. The product of sums (POS) form of the function F is

| A | B | C | D |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
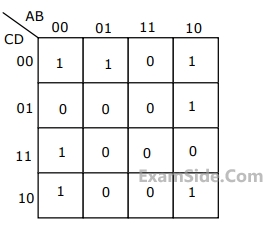
Marks 2


W= R+$$\overline P Q + \overline R $$ S
X = $$X = PQ\overline R \,\overline S + \overline P \,\overline Q \,\overline R \,\overline S + P\overline Q \,\overline R \,\overline S $$
Y = $$RS + \overline {OR + P\overline Q + \overline {PQ} } $$
Z = $$R + S + \overline {PQ + \overline {PQR} + P\overline {QS} } $$
Marks 4
Marks 5
By using an OR gate array as shown in figure where $${P_{1\,}}\,to\,{P_5}$$ are the product terms in one or more of the variables a, $$\overline a $$, b, $$\,\overline b $$, c and $$\overline c $$.

Marks 10

(A) draw K-map for outputs, W, X, Y, and Z.
(B) Obtain minimized expression for the outputs W, X, Y, and Z.