Transmission Lines · Electromagnetics · GATE ECE
Marks 1
1
Consider a lossless transmission line terminated with a short circuit as shown in the figure below. As one moves towards the generator from the load, the normalized impedances $Z_{inA}$, $Z_{inB}$, $Z_{inC}$, and $Z_{inD}$ (indicated in the figure) are ______.
GATE ECE 2024
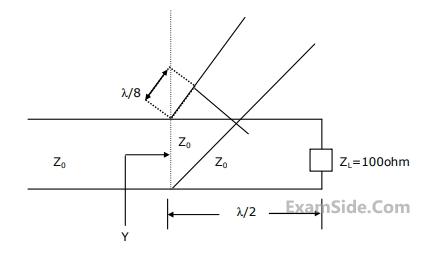
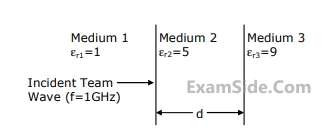
2
The voltage of an electromagnetic wave propagating in a coaxial cable with uniform characteristic impedance is $$V(l) = {e^{ - \gamma l\, + \,j\,\omega \,t}}$$ Volts, where $$l$$ is the distance along the length of the cable in metres, $$\gamma = (0.1\, + \,j40)\,\,{m^{ - 1}}$$ is the complex propagation constant, and $$\omega = \,2\,\pi \,\, \times \,\,{10^9}$$ rad/s is the angular frequency. The absolute value of the attenuation in the cable in dB/metre is ___________________.
GATE ECE 2017 Set 1
3
A two wire transmission line terminates in a television set. The VSWR measured on the line is 5.8. The percentage of power that is reflected from the television set is
GATE ECE 2017 Set 2
4
The propagation constant of a lossy transmission line is (2 + j5) $${m^{ - 1}}$$ and its characteristic impedance is (50 + j0) $$\Omega $$ at $$\omega = \,{10^6}\,rad\,{S^{ - 1}}$$. The values of the line constants L, C, R, G are, respectively,
GATE ECE 2016 Set 1
5
A coaxial cable is made of two brass conductors. The spacing between the conductors is filled with Teflon $$\left( {{\varepsilon _r} = 2.1,\,\,\tan \,\,\delta = \,0} \right)$$. Which one of the following circuits can represent the lumped element model of a small piece of this cable having length $$\Delta \,\,z\,\,?$$
GATE ECE 2015 Set 3
6
In the following figure, the transmitter Tx sends a wideband modulated RF signal via a coaxial cable to the receiver Rx. The output impedance $${Z_T}$$ of Tx, the characteristic impedance $${Z_0}$$ of the cable and the input impedance $${Z_R}$$ of Rx are all real.
Which one of the following statements is TRUE about the distortion of the received signal due to impedance mismatch?
Which one of the following statements is TRUE about the distortion of the received signal due to impedance mismatch?GATE ECE 2014 Set 3
7
To maximize power transfer, a lossless transmission line is to be matched to a resistive load impedance via a $$\lambda /4$$ transformer as shown.
GATE ECE 2014 Set 2
8
The return loss of a device is found to be 20 dB. The voltage standing wave ratio (VSWR) and magnitude of reflection coefficient are respectively.
GATE ECE 2013
9
A coaxial cable with an inner diameter of 1 mm and outer diameter of 2.4 mm is filled with a dielectric of relative permittivity 10.89. Given $${\mu _0} = \,4\,\pi \, \times \,{10^{ - 7}}$$
$$H/m,\,\,{\varepsilon _0} = {{{{10}^{ - 9}}\,} \over {36\,\pi }}\,F/m,$$ the characteristic impedance of the cable is
$$H/m,\,\,{\varepsilon _0} = {{{{10}^{ - 9}}\,} \over {36\,\pi }}\,F/m,$$ the characteristic impedance of the cable is
GATE ECE 2012
10
A transmission line of characteristic impedance 50 $$\Omega $$ is terminated by a 50 $$\Omega $$ load. When excited by a sinusoidal voltage source at 10 GHz, the phase difference between two points spaced 2 mm apart on the line is found to be $$\pi /4$$ radians. The phase velocity of the wave along the line is
GATE ECE 2011
11
If the scattering matrix [S] of a two port network is $$$\left[ S \right] = \left[ {\matrix{
{0.2\,\angle \,\,{0^ \circ }} & {0.9\,\,\angle \,\,{{90}^ \circ }} \cr
{0.9\,\angle \,\,{{90}^ \circ }} & {0.1\,\angle \,{{90}^ \circ }} \cr
} } \right]$$$
then the network is
GATE ECE 2010
12
A transmission line has a characteristic impedance of 50 $$\Omega $$ and a resistance of 0.1 $$\Omega $$/m. If the line is distortionless, the attenuation constant (in Np/m) is
GATE ECE 2010
13
Many circles are drawn in a Smith chart used for transmission line calculations. The circles shown in Fig. represent
GATE ECE 2005
14
In an impedance Smith chart, a clockwise movement along a constant resistance circle gives rise to
GATE ECE 2002
15
The VSWR can have any value between
GATE ECE 2002
16
A transmission line is distortionless if
GATE ECE 2001
17
The magnitudes of the open-circuit and short-circuit input impedances of a transmission line are 100$$\Omega \,$$ and 25$$\Omega \,$$ respectively. The characteristic impedance of the line is
GATE ECE 2000
18
Assuming perfect conductors of a transmission line, pure TEM propagation is NOT possible in
GATE ECE 1999
19
All transmission line sections shown in Fig. have characteristic impedance $${R_0}\, + \,j0$$. The input impedance $${Z_{in}}$$ equals
GATE ECE 1998
20
A transmission line of 50$$\Omega $$ characteristic impedance is terminated with a 100 $$\Omega $$ resistance. The minimum impedance measured on the line is equal to
GATE ECE 1997
21
A lossless transmission line having 50 $$\Omega $$ characteristic impedance and lenght $$\lambda /4$$ is short ciruited at one end and connected to an ideal voltage sourec of 1 V at the other end. The current drawn from the voltage source is
GATE ECE 1996
22
The capacitance per unit length and the characteristic impedance of a lossless transmission line are C and $$Z_0$$ respectively. The velocity of a traveling wave on the transmission line is
GATE ECE 1996
23
A load impedance (200 + j0) $$\Omega $$ is to be matched to a 50$$\Omega $$ lossless transmission line by using a quarter wave line transformer (QWT). The characteristic impedance of the QWT required is
GATE ECE 1994
Marks 2
1
A lossless transmission line with characteristic impedance $Z_0 = 50 \Omega$ is terminated with an unknown load. The magnitude of the reflection coefficient is $|\Gamma| = 0.6$. As one moves towards the generator from the load, the maximum value of the input impedance magnitude looking towards the load (in $\Omega$) is _________.
GATE ECE 2024
2
The standing wave ratio on a 50 $$\Omega$$ lossless transmission line terminated in an unknown load impedance is found to be 2.0. The distance between successive voltage minima is 30 cm and the first minimum is located at 10 cm from the load. $$Z_L$$ can be replaced by an equivalent length $$l_m$$ and terminating resistance $$R_m$$ of the same line. The value of $$R_m$$ and $$l_m$$, respectively, are
GATE ECE 2023
3
The following circuit(s) representing a lumped element equivalent of an infinitesimal sectioin of a transmission line is/are
GATE ECE 2023
4
A microwave circuit consisting of lossless transmission lines $$T_1$$ and $$T_2$$ is shown in the figure. The plot shows the magnitude of the input reflection coefficient $$\Gamma $$ as a function of frequency f. The phase velocity of the signal in the transmission lines is $$2\, \times \,{10^8}$$ m/s
GATE ECE 2016 Set 2
5
A lossless microstrip transmission line consists of a trace of width w. It is drawn over a practically infinite ground plane and is separated by a dielectric slab of thickness 𝑡 and relative permittivity $${\varepsilon _r}\, > \,1$$. The inductance per unit length and the characteristic impedance of this line are L and $$Z_o$$ respectively.
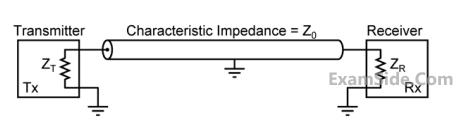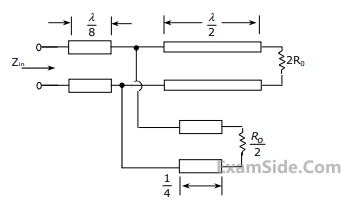
Which one of the following inequalities is always satisfied?
Which one of the following inequalities is always satisfied?GATE ECE 2016 Set 2
6
A 200 m long transmission line having parameters shown in the figure is terminated into a load ܴ$$R_L$$. The line is connected to a 400 V source having source resistance $$R_S$$ through a switch, which is closed at t = 0. The transient response of the circuit at the input of the line (z = 0) is also drawn in the figure. The value of ܴ$$R_L$$ (in $$\Omega $$ ) is ___________.
GATE ECE 2015 Set 3
7
Consider the 3 m long lossless air-filled transmission line shown in the figure. It has a characteristic impedance of $$120\pi \,\Omega $$, is terminated by a short circuit, and is excited with a frequency of 37.5 MHz. What is the nature of the input impedance $$({Z_{in}})$$?
GATE ECE 2015 Set 3
8
In the transmission line shown, the impedance $${Z_{in}}$$ (in ohms) between node A and the ground is
GATE ECE 2014 Set 2
9
For a parallel plate transmission line, let v be the speed of propagation and Z be the characteristic impedance. Neglecting fringe effects, a redution of the spacing between the plates by a factor of two results in
GATE ECE 2014 Set 1
10
A transmission line with a characteristic impedance of 100 $$\Omega $$ is used to match a 50 $$\Omega $$ section to a 200 $$\Omega $$ section. If the matching is to be done both at 429 MHz and 1 GHz, the tength of the transmission line can be approximately
GATE ECE 2012
11
A transmission line of characteristic impedance 50 $$\Omega $$ is terminated in a load impedance $$Z_L$$. The VSWR of the line is measured as 5 and the first of the voltage naxima in the line is observed at a distance of $$\lambda /4$$ from the load. The value of $$Z_L$$ is
GATE ECE 2011
12
In the circuit shown, all the transmission line sections are lossless. The Voltage Standing Wave Ration (VSWR) on the 60W line is
GATE ECE 2010
13
A transmission line terminates in two branches, each of length $$\lambda /4$$, as shown.The branches are terminated by 50 $$\Omega $$ loads. The lines are lossless and have the characteristic impedances shown. Determine the impedance $${Z_i}$$ as seen by the source.
GATE ECE 2009
14
One end of loss-less transmission line having the characteristic impedance of 75 $$\Omega $$ and length of 1 cm is short-ciruited. At 3 GHz, the input impedance at the other end of the transmission line is
GATE ECE 2008
15
The parallel branches of a 2-wire transmission line are terminated in 100 $$\Omega $$ and 200 $$\Omega $$ resistors as shown in the Fig. The characteristic impedance of the line is $$Z_0$$ = 50 $$\Omega $$ and each section has a length of $$\lambda /4$$. The voltage reflection coefficient $$\Gamma $$ at the input is:
GATE ECE 2007
16
A load of 50 $$\Omega $$ is connected in shunt in a 2-wire transmission line of $$Z_0$$ = 50 $$\Omega $$ as shown in the Fig. The 2-port scattering parameter matrix (S-matrix) of the shunt element is
GATE ECE 2007
17
Characteristic impedance of a transmission line is 50$$\Omega $$. Input impedance of the open-circuited line is $${Z_{oc}} = 100\, + \,j\,\,150\Omega .$$ When the transmission line is short-circuited the value of the input impedance will be
GATE ECE 2005
18
Voltage standing wave pattern in a lossless transmission line with characteristic impedance 50 $$\Omega $$ and a resistive load is shown in Fig.
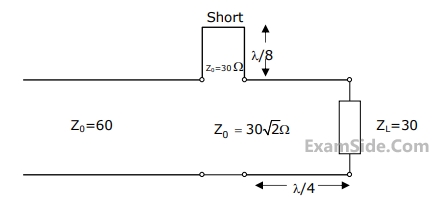
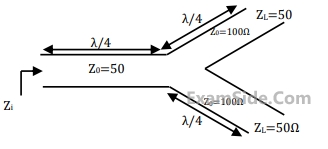
The reflection coefficient is given by
The reflection coefficient is given by GATE ECE 2005
19
Voltage standing wave pattern in a lossless transmission line with characteristic impedance 50 $$\Omega $$ and a resistive load is shown in Fig.
The value of the load resistance is
The value of the load resistance is GATE ECE 2005
20
Consider a 300$$\Omega $$, quarter-wave long (at 1 GHz) transmission line as shown in Fig. It is connected to a 10V, 50$$\Omega $$ sources at one end and is left open circuited at the other end. The magnitude of the voltage at the open circuit end of the line is
GATE ECE 2004
21
Consider an impedance Z = R + jX marked with point P in an impedance Smith chart as shown in Fig. The movement from point P along a constant resistance circle in the clockwise direction by an angle $${45^ \circ }$$ is equivalent to
GATE ECE 2004
22
A lossless transmission line is terminated in a load which reflects a part of the incident power. The measured VSWR is 2. The percentage of the power that is reflected back is
GATE ECE 2004
23
A short-circuited stub is shunt connected to a transmission line as shown in Fig. If $${Z_0} = 50\,\,\Omega $$, the admittance Y seen at the junction of the stub and the transmission line is
GATE ECE 2003
24
In air, a lossless transmission line of length 50 cm with $$L = 10\,\mu H/m,\,\,C = 40\,\,pF/m$$ is operated at 25 MHz. Its electrical path length is
GATE ECE 1999
25
In a twin-wire transmission line in air, the adjacent voltage maxima are at 12.5 cm and 27.5. The operating frequency is
GATE ECE 1999
26
If a pure resistance load, when connected to a lossless 75-ohm line, produces a VSWR of 3 on the line, then the load impedance can only be 25 ohms.
GATE ECE 1994
27
Consider a transmission line of characteristic impedance 50 ohm. Let it be terminated at one end by ( + j50) ohm. The VSWR produced by it in the transmission line will be
GATE ECE 1993
28
A transmission line whose characteristic impedance is a pure resistance
GATE ECE 1992
29
The input impedance of a short-circuited lossless transmission line guarter wave long is
GATE ECE 1991
30
A 50 ohm lossless transmission line has a pure reactance of (j100) ohms as its load. The VSWR in the line is :
GATE ECE 1989
31
A two - wire transmission line of characteristic impedance $$Z_0$$ is connected to a load of impedance $${Z_L}({Z_L}\, \ne \,\,{Z_0})$$. Impedance matching cannot be achieved with
GATE ECE 1988
32
A transmission line of pure resistive characteristic impedance is terminated with an unknown load. The measured value of VSWR on the line is equal to 2 and a voltage minimum point is found to be at the load. The load impedance is then
GATE ECE 1987
Marks 5
1
The three regions shown in Fig. are all lossless and non-magnetic. Find
(a) Wave impedance in mediums 2 and 3.
(b) d such that medium 2 acts as a quarter wave $$(\lambda /40$$)transformer.
(c) Reflection coefficient $$(\Gamma )$$ and voltage standing wave ratio (VSWR) at the interface of the medium 1 and 2, when $$d = \lambda /4$$.
GATE ECE 2000
2
A $${\lambda \over 2}$$ section of a 600 $$\Omega $$ transmission line, short ciruited at one end and open circuited at the other end, is shown in Fig. A 100 V / 75 $$\Omega $$ generator is connected at the mid point of the section as shown in the Fig. Find the voltage at the open-ciruited end of the line.
GATE ECE 1997