Compensators · Control Systems · GATE ECE
Marks 1
where k, a and b are positive real numbers. The condition for this controller to act as a phase lead compensator is
where T > 0. The maximum phase-shift provided by such a compesator is
Marks 2
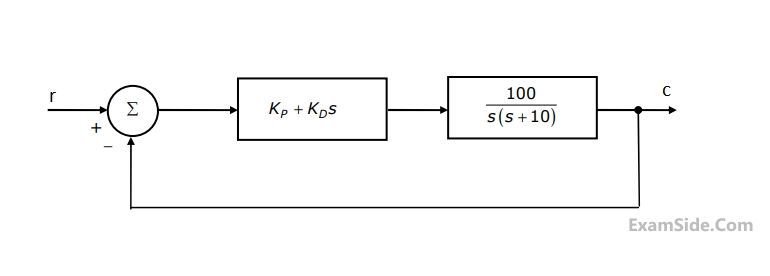
Let $G(s)=\frac{1}{10 s^2}$ be the transfer function of a second-order system. A controller $M(s)$ is connected to the system $G(s)$ in the configuration shown below. Consider the following statements.
(i) There exists no controller of the form $M(s)=\frac{K_I}{s}$, where $K_I$ is a positive real number, such that the closed loop system is stable.
(ii) There exists at least one controller of the form $M(s)=K_P+s K_D$, where $K_P$ and $K_D$ are positive real numbers, such that the closed loop system is stable.
Which one of the following options is correct?

A satellite attitude control system, as shown below, has a plant with transfer function $G(s) = \frac{1}{s^2}$ cascaded with a compensator $C(s) = \frac{K(s +\alpha)}{s + 4}$, where $K$ and $\alpha$ are positive real constants.

In order for the closed-loop system to have poles at $-1 \pm j \sqrt{3}$, the value of $\alpha$ must be ______.
Kt=1 N-m/A, Ra=$$1\Omega ,$$ La=0.1H,
J=5kg-m2, B=1 N-m/(rad/sec) and Kb=1V/(rad/sec).
The steady-state position response (in radians) due to unit impulse disturbance torque Td is ____.

The phase of the above lead compensator is maximum at
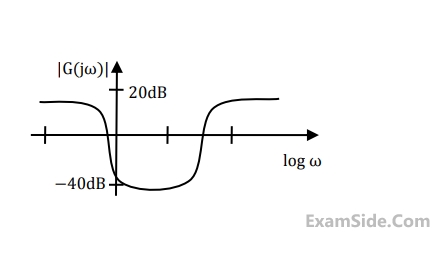
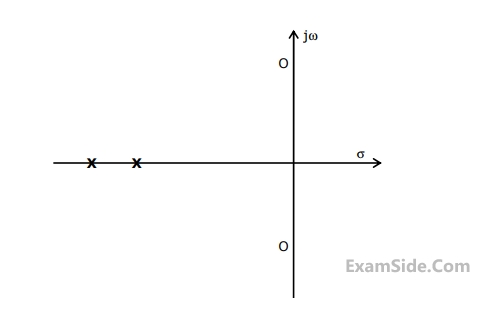
$${G_C}(s)$$ is a lead compensator if
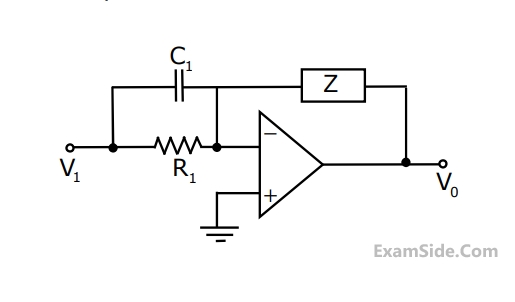 Group - I
Group - I
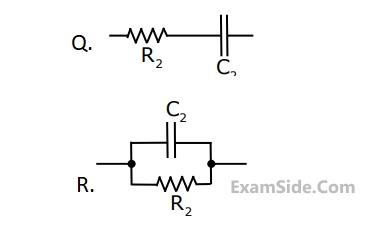
Group - II
1. PID controller
2. Lead compensator
3. Lag compensator
The condition for the RC network to act as a phase lead controller is:
Marks 5
(a) Determine the frequency at which the plant has a phase lah of 90o.
(b) An intergral controller with transfer function Gc(s)=$${k \over s}$$ , isplaced in the forwardpath the value of k such that the compensated system has an open loop gain margin of 2.5.
(c) Determine the steady state errors of the compensated system to unit-step and unit-ramp inputs.

(a) Find the desired location of the closed loop poles.
(b) Write down the requiredcharacteristic equation for the system. Hense determine the PD controller transfer function Gp(s) when K = 1.
(c) Sketch the root-locus for the system.
