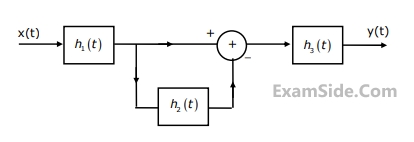
Continuous Time Linear Invariant System · Signals and Systems · GATE ECE

The input x(t) and the output y(t) of a continuous time system are related as $$y\left( t \right) = \int\limits_{t - T}^t {x\left( u \right)du.} $$. The system is

Consider the following statements for continuous-time linear time invariant (LTI) system.

I. There is no bounded input bounded output (BIBO) stable system with a pole in the right half of the complex plane.
II. There is no causal and BIBO stable system with a pole in the right half of the complex plane.

Which one among the following is correct?

The impulse response of an LTI system can be obtained by

The result of the convolution $$x\left( { - t} \right) * \delta \left( { - t - {t_0}} \right)$$ is

The impulse response of a system is h(t) = t u(t). For an input u(t - 1), the output is

Two system with impulse responses h₁(t) and h₂(t) are connected in cascade. Then the overall impulse response of the cascaded system is given by

The differential equation $$100{{{d^2}y} \over {dt}} - 20{{dy} \over {dt}} + y = x\left( t \right)$$ describes a system with an input x(t) and output y(t). The system, which is initially relaxed, is excited by a unit step input. The output y(t) can be represented by the waveform

The impulse response h(t) of a linear time-invariant continuous time system is described by $$h\left( t \right) = \,\,\exp \left( {\alpha t} \right)u\left( t \right)\,\,\, + \,\,\exp \left( {\beta t} \right)u\left( { - t} \right),$$ where u(t) denotes the unit step function, and $$\alpha $$ and $$\beta $$ are real constants. This system is stable if

The input and output of a continuous system are respectively denoted by x(t) and y(t). Which of the following descriptions corresponds to a causal system?

Which of the following can be impulse response of a causal system?

Let x(t) be the input to a linear, time-invariant system. The required output is 4x(t - 2). The transfer function of the system should be

Convolution of x(t + 5) with impulse function $$\delta \left( {t\, - \,7} \right)$$ is equal to

The transfer function of a system is given by $$H\left( s \right) = {1 \over {{s^2}\left( {s - 2} \right)}}$$. The impulse response of the system is

A system with an input x(t) and an output y(t) is described by the relation: y(t) = t x(t). This system is

The unit impulse response of a linear time invariant system is the unit step function u(t). For t>0, the response of the system to an excitation e^-at u(t), a>0 will be

The transfer function of a zero - order - hold system is

The transfer function of a linear system is the

Non - minimum phase transfer function is defined as the transfer function

Let h(t) be the impulse response of a linear time invariant system. Then the response of the system for any input u(t) is

Indicate whether the following statement is TRUE/FALSE: Give reason for your answer.

If G(s) is a stable transfer function, then $$F\left( s \right) = {1 \over {G\left( s \right)}}$$ is always a stable transfer function.

The transfer function of a causal LTI system is H(s) = 1/s. If the input to the system is x(t) = $$\left[ {\sin (t)/\pi t} \right]u(t);$$ where u(t) is a unit step function. The system output y(t) as $$t \to \infty $$ is _____________________.

Consider the parallel combination of two LTI systems shown in the figure.

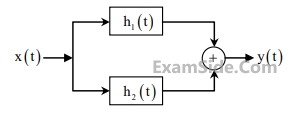
The impulse responses of the systems are

$${h_1}(t) = 2\delta (t + 2)\, - 3\delta (t + 1)$$
$${h_2}(t) = \delta (t - 2)$$
If the input x(t) is a unit step signal, then the energy of y(t) is__________________.

Consider an LTI system with magnitude response $$$\left| {H(f)} \right| = \left\{ {\matrix{ {1 - \,{{\left| f \right|} \over {20}},} & {\left| f \right| \le 20} \cr {0,} & {\left| f \right| > 20} \cr } } \right.$$$ and phase response Arg[H(f)]= - 2f.
If the input to the system is $$x(t) = 8\cos \left( {20\pi t + \,{\pi \over 4}} \right) + \,16\sin \left( {40\pi t + {\pi \over 8}} \right) + 24\,\cos \left( {80\pi t + {\pi \over {16}}} \right)$$
Then the average power of the output signal y(t) is_____________.

A continuous time signal x(t) = $$4\cos (200\pi t)$$ + $$8\cos(400\pi t)$$, where t is in seconds, is the input to a linear time invariant (LTI) filter with the impulse response $$h(t) = \left\{ {{{2\sin (300\pi t)} \over {\matrix{ {\pi t} \cr {600} \cr } }}} \right.\,,\,\matrix{ t \cr t \cr } \,\matrix{ \ne \cr = \cr } \,\matrix{ 0 \cr 0 \cr } $$

Let y(t) be the output of this filter. The maximum value of $$\left| {y(t)} \right|$$ is ________________________.

The output of a standrad second-order system for a unit step input is given as $$y(t) = 1 - {2 \over {\sqrt 3 }}{e^{ - t}}\cos \left( {\sqrt 3 t - {\pi \over 6}} \right)$$.

The transfer function of the system is

Input x(t) and output y(t) of an LTI system are related by the differential equation y"(t) - y'(t) - 6y(t) = x(t). If the system is neither causal nor stable, the imulse response h(t) of the system is

The impulse response of a continuous time system is given by $$h(t) = \delta (t - 1) + \delta (t - 3)$$. The value of the step response at t = 2 is

The input x(t) and output y(t) of a system are related as y(t) = $$\int\limits_{ - \infty }^t x (\tau )\cos (3\tau )d\tau $$.

The system is

An input x(t) = exp( -2t) u(t) + $$\delta $$(t-6) is applied to an LTI system with impulse response h(t) = u(t). The output is

A continuous time LTI system is described by $${{{d^2}y(t)} \over {d{t^2}}} + 4{{dy(t)} \over {dt}} + 3y(t)\, = 2{{dx(t)} \over {dt}} + 4x(t)$$.

Assuming zero initial conditions, the response y(t) of the above system for the input x(t) = $${e^{ - 2t}}$$ u(t) is given by

Consider a system whose input x and output y are related by the equation $$$y(t) = \int\limits_{ - \infty }^\infty {x(t - \tau )\,h(2\tau )\,d\tau } $$$

Where h(t) is shown in the graph.

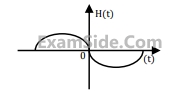
Which of the following four properties are possessed by the system?

BIBO: Bounded input gives a bounded output.
Causal: The system is casual.
LP: The system is low pass.
LTI: The system is linear and time- invariant.

Let x(t) be the input and y(t) be the output of a continuous time system. Match the system properties P1, P2 and P3 with system relations R1, R2, R3, R4.

Properties

P1 : Linear but NOT time-invariant
P2: Time-invariant but NOT linear
P3: Linear and time-invariant

Relations

R1: y(t) = $${t^2}$$ x(t)
R2: y(t) = t$$\left| {x(t)} \right|$$
R3: y(t) = $$\left| {x(t)} \right|$$
R4: y(t) = x(t-5)

A linear, time-invariant, causal continuous time system has a rational transfer function with simple poles at s = - 2 and s = - 4, and one simple zero at s = - 1. A unit step u(t) is applied at the input of the system. At steady state, the output has constant value of 1. The impulse response of this system is

The frequency response of a linear, time-invariant system is given by H(f) = $${5 \over {1 + j10\pi f}}$$. The step response of the system is

Let g(t) = p(t) * p(t), where * denotes convolution and p(t) = u(t) - (t-1) with u(t) being the unit step function. The impulse response of filter matched to the singal s(t) = g(t) - $$[\delta (t - 2)*g(t)]$$ is given as

The output y(t) of a linear time invariant system is related to its input x(t) by the following equation: y(t) = 0.5 x $$(t - {t_d} + T) + \,x\,(t - {t_d}) + 0.5\,x(t - {t_d} - T)$$. The filter transfer function $$H(\omega )$$ of such a system is given by

A system described by the differential equation: $${{{d^2}y} \over {d{t^2}}} + 3{{dy} \over {dt}} + 2y = x(t)$$ is initially at rest. For input x(t) = 2u(t), the output y(t) is

A rectangular pulse train s(t) as shown in Fig.1 is convolved with the signal $${\cos ^2}$$ ($$4\pi \,{10^{3\,}}$$t). The convolved signal will be a

A causal system having the transfer function H(s) = $${1 \over {s + 2}}$$, is excited with 10 u(t). The time at which the output reaches 99% of its steady state value is

The impulse response function of four linear system S1, S2, S3, S4 are given respectively by

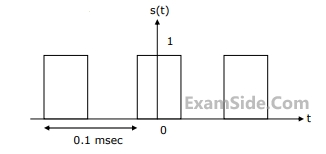
$${h_1}$$(t), = 1;

$${h_2}$$(t), = U(t);

$${h_3}(t)\, = \,{{U(t)} \over {t + 1}}$$;

$${h_4}(t)\, = {e^{ - 3t}}U(t)$$ ,

where U (t) is the unit step function. Which of these system is time invariant, causal, and stable?

Let u(t) be the unit step function. Which of the waveforms in Fig.(a) -(d) corresponds to the convolution of $$\left[ {u\left( t \right)\, - \,u\left( {t\, - \,1} \right)} \right]$$ with $$\left[ {u\left( t \right)\, - \,u\left( {t\, - \,2} \right)} \right]$$ ?

A linear time invariant system has an impulse response $${e^{2t}},\,\,t\, > \,0.$$ If the initial conditions are zero and the input is $${e^{3t}}$$, the output for $$t\, > \,0$$ is

Match each of the items 1, 2 on the left with the most appropriate item A, B, C or D on the right.

In the case of a linear time invariant system

List - 1
(1) Poles in the right half plane implies.
(2) Impulse response zero for $$t \le 0$$ implies.

List - 2
(A) Exponential decay of output
(B) System is causal
(C) No stored energy in the system
(D) System is unstable

Match each of the items A, B and C with an appropriate item from 1, 2, 3, 4 and 5.

List - 1
(A) $${a_1}{{{d^{2y}}} \over {d{x^2}}} + {a_2}y{{dy} \over {dx}} + {a_3}y = {a_4}$$
(B) $${a_1}{{{d^3}y} \over {d{x^3}}} + {a_2}y = {a_3}$$
(C) $$\eqalign{ & {a_1}{{{d_2}y} \over {d{x_2}}} + {a_2}x{{dy} \over {dx}} + {a_3}\,{x^2}y = 0 \cr & \cr} $$

List - 2
(1) Non linear differential equation.
(2) Linear differential equation with constant coefficients.
(3) Linear homogeneous differential equation.
(4) Non - Linear homogeneous differential equation.
(5) Non - linear first order differential equation.

The voltage across an impedance in a network is V(s) = Z(s) I(s), where V(s), Z(s) and $${\rm I}$$(s) are the Laplace Transforms of the corresponding time functions V(t), z(t) and i(t).

The voltage v(t) is

An excitation is applied to a system at $$t = T$$ and its response is zero for $$ - \infty < t < T$$. Such a system is a

The impulse response and the excitation function of a linear time invariant casual system are shown in Fig. a and b respectively. The output of the system at t = 2 sec. is equal to

The response of an initially relaxed linear constant parameter network to a unit impulse applied at $$t = 0$$ is $$4{e^{ - 2t}}u\left( t \right).$$ The response of this network to a unit step function will be:

The transfer function of a zero-order hold is

A deterministic signal x(t) = $$\cos (2\pi t)$$ is passed through a differentiator as shown in Figure.
(a) Determine the autocorrelation R_xx ($$\tau $$) and the power spectral density S_xx(f).
(b) Find the output power spectral density S_yy( f ).
(c) Evaluate R_xy(0) and R_xy(1/4).

For the linear, time-invariant system whose block diagram is shown in Fig.(a), with input x(t) and output y(t).

(a) Find the transfer function.
(b) For the step response of the system [i.e. find y(t) when x(t) is a unit step function and the initial conditions are zero]
(c) Find y(t), if x(t) is as shown in Fig.(b), and the initial conditions are zero.

Fig.1, shows the block diagram representation of a control system. The system in block A has an impulse response $${h_A}(t) = {e^{ - t}}\,u(t)$$. The system in block B has an impulse response $${h_B}(t) = {e^{ - 2t}}\,u(t)$$. The block 'k' amplifies its input by a factor k. For the overall system with input x(t) and output y(t)

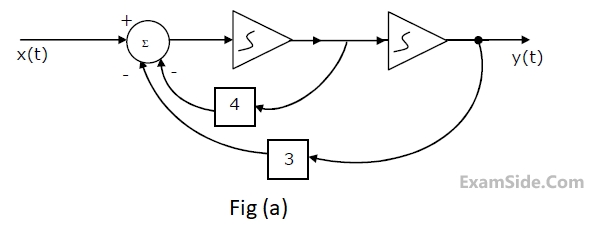
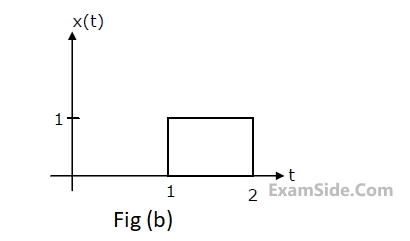
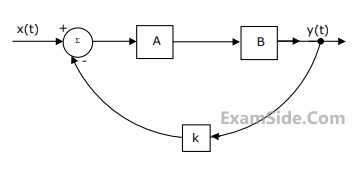
(a) Find the transfer function $${{Y(s)} \over {X(s)}}$$, when k=1

(b) Find the impulse response, when k = 0

(c) Find the value of k for which the system becomes unstable.

$$$\left[ {\matrix{ {Note:u(t)\, \equiv \,0} & {t\, \le \,0} \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \equiv 1} & {t\, > \,0} \cr } } \right]$$$

Consider the following interconnection of the three LTI systems (Fig.1). $${h_1}(t)$$ , $${h_2}(t)$$ and $${h_3}(t)$$ are the impulse responses of these three LTI systems with $${H_1}(\omega )$$, $${H_2}(\omega )$$, and $${H_3}(\omega )$$ as their respective Fourier transforms. Given that $${h_1}\,(t)\, = \,{d \over {dt}}\left[ {{{\sin ({\omega _0}t)} \over {2\,\pi \,t}}} \right],{H_2}(\omega ) = \exp \left( {{{ - j2\pi \omega } \over {{\omega _0}}}} \right)$$
$${h_3}\,(t)\, = u(t)\,and\,x(t)\, = \,\sin \,2\,{\omega _0}t\, + \,\cos \,({\omega _0}t/2),$$ find the output y(t).