Stability · Control Systems · GATE ECE
Marks 1
1
The Nyquist stability criterion and the Routh criterion both are powerful analysis tools for
determining the stability of feedback controllers. Identify which of the following statements
is FALSE.
GATE ECE 2018
2
Consider p(s) = s3 + $${a_2}$$s2 + $${a_1}$$s + $${a_0}$$ with all real coefficients. It is known that its
derivative p'(s) has no real roots. The number of real roots of p(s) is
GATE ECE 2018
3
Match the inferences X, Y, and Z, about a system, to the corresponding properties of the
elements of first column in Routh's Table of the system characteristic equation.
X: The system is stable …
Y: The system is unstable …
Z: The test breaks down …
P: … when all elements are positive
Q: … when any one element is zero
R: … when there is a change in sign of
coefficients
GATE ECE 2016 Set 1
4
A unity negative feedback system has the open-loop transfer function
$$$G\left(s\right)\;=\;\frac K{s\left(s\;+\;1\right)\left(s\;+\;3\right)}$$$
The value of the gain K (>0) at which the root locus crosses the imaginary axis is _________.
GATE ECE 2015 Set 1
5
The forward path transfer function of a unity negative feedback system is given by
$$$G\left(s\right)\;=\;\frac k{\left(s\;+\;2\right)\left(s\;-\;1\right)}$$$
The value of K which will place both the poles of the closed-loop system at the same
location, is ______.
GATE ECE 2014 Set 1
6
A polynomial $$f\left(x\right)\;=\;a_4x^4\;+\;a_3x^3\;+\;a_2x^2\;+\;a_1x\;-\;a_0$$ with all coefficients positive has
GATE ECE 2013
7
Which one of the following statements is NOT TRUE for a continuous time causal
and stable LTI system?
GATE ECE 2013
8
An amplifier with resistive negative feedback has two left half-plane poles in its
open-loop transfer function. The amplifier
GATE ECE 2000
9
A system described by the transfer function
$$$H\left(s\right)=\frac1{s^3+\alpha s^2+ks+3}$$$ is stable. The constraints on $$\alpha$$ and k are,
GATE ECE 2000
10
The number of roots of $$s^3\;+\;5s^2\;+\;7s\;+\;3\;=\;0$$ in the left half of the s-plane are
GATE ECE 1998
11
The open loop transfer function of a unity feedback open-loop system is $$\frac{2s^2+6s+5}{\left(s+1\right)^2\left(s+2\right)}$$. The characteristic equation of the closed loop system is
GATE ECE 1998
Marks 2
1
Consider the polynomial $p(s)=s^5+7 s^4+3 s^3-33 s^2+2 s-40$. Let $(L, I, R)$ be defined as follows.
$L$ is the number of roots of $p(s)$ with negative real parts.
$I$ is the number of roots of $p(s)$ that are purely imaginary.
$R$ is the number of roots of $p(s)$ with positive real parts.
Which one of the following options is correct?
GATE ECE 2025
2
Consider an even polynomial p(s) given by
$$p(s) = {s^4} + 5{s^2} + 4 + K$$
where K is an unknown real parameter. The complete range of K for which p(s) has all its roots on the imaginary axis is __________.
GATE ECE 2022
3
A unity feedback control system is characterized by the open-loop transfer function
$$$G\left(s\right)\;=\;\frac{2\left(s+1\right)}{s^3+ks^2+2s+1}$$$
The value of k for which the system oscillates at 2 rad/s is ________.
GATE ECE 2017 Set 2
4
Which one of the following options correctly describes the locations of the roots of the
equation s4 + s2 + 1 = 0
on the complex plane?
GATE ECE 2017 Set 1
5
The first two rows in the Routh table for the characteristic equation of a certain closed-loop control
system are given as
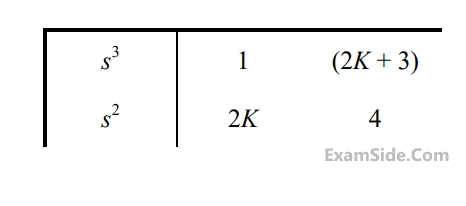 The range of K for which the system is stable is
The range of K for which the system is stable is
 The range of K for which the system is stable is
The range of K for which the system is stable isGATE ECE 2016 Set 3
6
The transfer function of a linear time invariant system is given by $$H\left(s\right)\;=\;2s^4\;-\;5s^3\;+\;5s\;-\;2$$.
The number of zeros in the right half of the s-plane is __________.
GATE ECE 2016 Set 1
7
The characteristic equation of an LTI system is given by
F(s) = s5 + 2s4 +3s3 + 6s2 - 4s - 8 = 0.The number of roots that lie strictly in the left half s-plane is _____.
F(s) = s5 + 2s4 +3s3 + 6s2 - 4s - 8 = 0.The number of roots that lie strictly in the left half s-plane is _____.
GATE ECE 2015 Set 3
8
A plant transfer function is given as $$$G\left(s\right)=\left(K_p+\frac{K_1}s\right)\left(\frac1{s\left(s+2\right)}\right)$$$
. When the plant operates in a
unity feedback configuration, the condition for the stability of the closed loop system is
GATE ECE 2015 Set 1
9
Consider a transfer function $$G_p\left(s\right)\;=\;\frac{ps^2+3ps\;-2}{s^2+\left(3+p\right)s\;+\left(2-p\right)}$$ with 'p' a positive real parameter.
The maximum value of 'p' until which Gp remains stable is ________.
GATE ECE 2014 Set 4
10
The feedback system shown below oscillates at 2 rad/s when
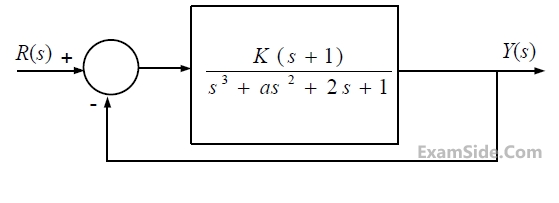
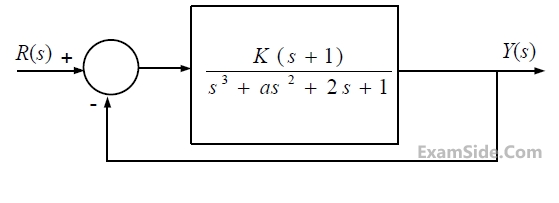
GATE ECE 2012
11
A certain system has transfer function $$G\left(s\right)=\frac{s+8}{s^2+\alpha s-4}$$, where $$\alpha$$
is a parameter.
Consider the standard negative unity feedback configuration as shown below
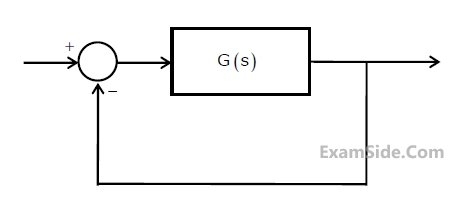 Which of the following statements is true?
Which of the following statements is true?
 Which of the following statements is true?
Which of the following statements is true?GATE ECE 2008
12
The number of open right half plane poles of $$$G\left(s\right)\;=\;\frac{10}{s^5\;+2s^4\;+3s^3\;+6s^2\;+5s\;+3}\;is$$$
GATE ECE 2008
13
The positive values of “K” and “a” so that the system shown in the figure below
oscillates at a frequency of 2 rad/sec respectively are
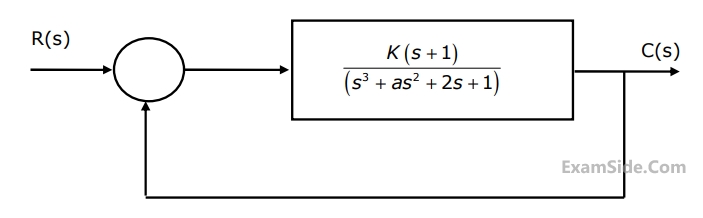

GATE ECE 2006
14
For the polynomial
P(s) = s5 + s4 + 2s3 + 2s2 + 3s + 15 ,
the number of roots which lie in the right half of the s-plane is
P(s) = s5 + s4 + 2s3 + 2s2 + 3s + 15 ,
the number of roots which lie in the right half of the s-plane is
GATE ECE 2004
15
The open-loop transfer function of a unity feedback system is $$$G\left(s\right)=\frac k{s\left(s^2+s+2\right)\left(s+3\right)}$$$ the range of 'k' for which the system is stable
GATE ECE 2003
16
The characteristic polynomial of a system is
q(s) = 2s5 + s4 + 4s3 + 2s2 + 2s + 1. The system is
q(s) = 2s5 + s4 + 4s3 + 2s2 + 2s + 1. The system is
GATE ECE 2002
17
The system shown in Figure remains stable when
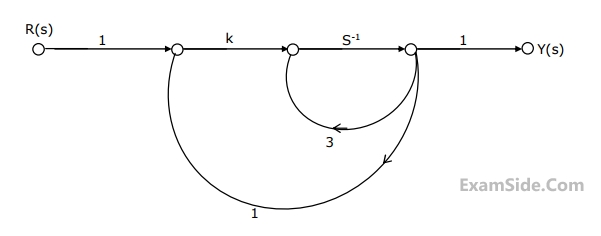

GATE ECE 2002
18
The feedback control system in Figure is stable
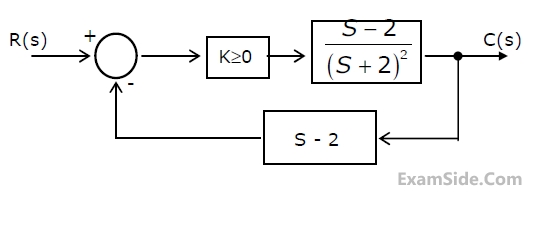

GATE ECE 2001
19
If G(s) is a stable transfer function, then $$F\left(s\right)=\frac1{G\left(s\right)}$$ is always a stable transfer
function.
GATE ECE 1994
20
If $$s^3+\;3s^2\;+\;4s\;+A\;=\;0$$ ,then all the roots of this equation are in the left half plane
provided that
GATE ECE 1993
21
An electromechanical closed-loop control system has the following characteristic equation $$s^3+6Ks^2+\left(K+2\right)s+8\;=\;0$$, where K is the forward gain of the system.The condition for closed loop stability is
GATE ECE 1990
22
In order to stabilize the system shown in fig. Ti should satisfy:


GATE ECE 1989
23
Consider a characteristic equation given by
s4 + 3s3 + 5s2 + 6s + K + 10 = 0.
The condition for stability is
s4 + 3s3 + 5s2 + 6s + K + 10 = 0.
The condition for stability is
GATE ECE 1988
Marks 5
1
Consider the feedback control system shown in figure.
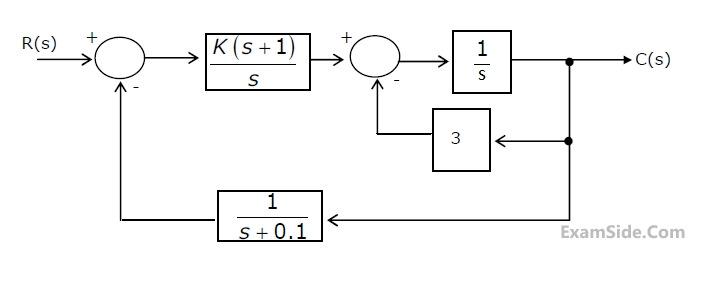
(a) Find the transfer function of the system and its characteristic equation.

(a) Find the transfer function of the system and its characteristic equation.
(b) Use the Routh-Hurwitz criterion to determine the range of 'K' for which the system is stable.
GATE ECE 2001
2
The loop transfer function of a feedback control system is given by $$$G\left(s\right)H\left(s\right)=\frac{K\left(s+1\right)}{s\left(1+Ts\right)\left(1+2s\right)},\;K>0$$$ Using Routh-Hurwitz criterion, determine the region of K-T plane in which the
closed-loop system is stable.
GATE ECE 1999
3
The characteristic equation of a feedback control system is
$$$s^4+20s^3+15s^2+2s+K\;=\;0$$$
(i) Determine the range of K for the system to be stable.
(ii) Can the system be marginally stable? If so, find the required value of K and the frequency of sustained oscillation.
(i) Determine the range of K for the system to be stable.
(ii) Can the system be marginally stable? If so, find the required value of K and the frequency of sustained oscillation.
GATE ECE 1998
4
A system having an open loop transfer function
$$G\left(s\right)=\frac{K\left(s+3\right)}{s\left(s^2+2s+2\right)}$$
is used in a
control system with unity negative feedback. Using the Routh-Hurwitz criterion,
find the range of values of 'K' for which the feedback system is stable.
GATE ECE 1996