Noise In Digital Communication · Communications · GATE ECE
Marks 1
for transmission of bits. The graphical representation of the matched filter output y(t) for this signal will be
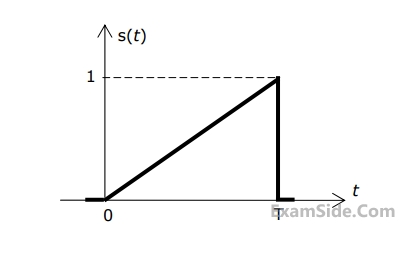
Marks 2
A source transmits symbol $S$ that takes values uniformly at random from the set $\{-2,0,2\}$. The receiver obtains $Y=S+N$, where $N$ is a zero-mean Gaussian random variable independent of $S$. The receiver uses the maximum likelihood decoder to estimate the transmitted symbol $S$.
Suppose the probability of symbol estimation error $P_e$ is expressed as follows:
$$ P_e=\alpha P(N>1), $$
where $P(N>1)$ denotes the probability that $N$ exceeds 1 .
What is the value of $\alpha$ ?
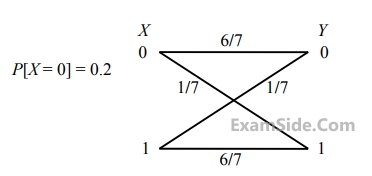
$${f_{\left. R \right|o}}\,(r) = \left\{ {\matrix{ {{1 \over 4},} & { - \,3\,\, \le \,\,x\,\, \le \,\,1,\,} \cr 0 & {otherwise,} \cr } } \right.and$$
$${f_{R/o}}\,(r) = \left\{ {\matrix{ {{1 \over 6},} & { - \,1\,\, \le \,\,x\,\, \le \,\,5\,,} \cr 0 & {otherwise.} \cr } } \right.$$
The minimum decision error orobability is
use $$Q\,(v) \approx \,{e^{ - {v^2}/2}}$$
When $$\beta = - \,0.3,\,$$ the BER is closed to
and $$${s_2}\left( t \right) = - \sqrt {{{2E} \over T}\,\sin \left( {{\omega _c}t} \right)} $$$
over the symbol interval, $$(0, T)$$. If the local oscillator in a coherent receiver is ahead in phase by 450 with respect to the received signal, the probability of error in the resulting system is
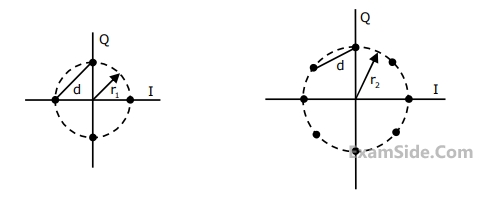
For the constraint that the minimum distance between pairs of signal points be d for both constellations, the radii r1, and r2 of the circles are

Assuming high SNR and that all signals are equally probable, the additional average transmitted signal energy required by the 8-PSK signal to achieve the same error probability as the 4-PSK signal is
$${Y_k} = {N_k}$$ if transmitted bit $${b_k} = 0$$
$${Y_k} = a + {N_k}$$ if transmitted bit $${b_k} = 1$$
Where $${b_k} = 0$$ represents the noise sample value. The noise sample has a probability density function, $${P_{{N_k}}}\left( n \right)\,\,\,\,\,\,\, = 0.5\alpha {e^{ - \alpha \left| n \right|}}$$ (This has mean zero and variance $$2/{\alpha ^2}$$). Assume transmitted bits to be equiprobable and threshold $$z$$ is set to $$a/2 = {10^{ - 6}}V$$.
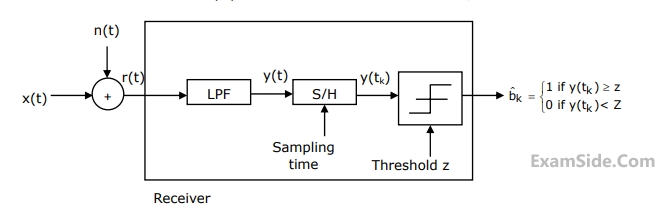
The value of the parameter $$\alpha $$( in V-1 ) is
$${Y_k} = {N_k}$$ if transmitted bit $${b_k} = 0$$
$${Y_k} = a + {N_k}$$ if transmitted bit $${b_k} = 1$$
Where $${b_k} = 0$$ represents the noise sample value. The noise sample has a probability density function, $${P_{{N_k}}}\left( n \right)\,\,\,\,\,\,\, = 0.5\alpha {e^{ - \alpha \left| n \right|}}$$ (This has mean zero and variance $$2/{\alpha ^2}$$). Assume transmitted bits to be equiprobable and threshold $$z$$ is set to $$a/2 = {10^{ - 6}}V$$.

The probability of bit error is
If the signal to quantization noise ratio required in uniformly quantizing the signals is 43.5 dB, the step size of the quantization is approximately
If the positive values of the signal are uniformly quantized with a step size of 0.05 V, and the negative values are uniformly quantized with a step size of 0.1V, the resulting signal to quantization noise ratio is approximately
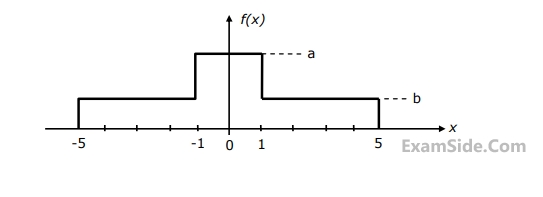
The values of a and b are

Assuming that the reconstruction levels of the quantizer are the mid-points of the decision boundaries, the ratio of signal power to quantization noise power is
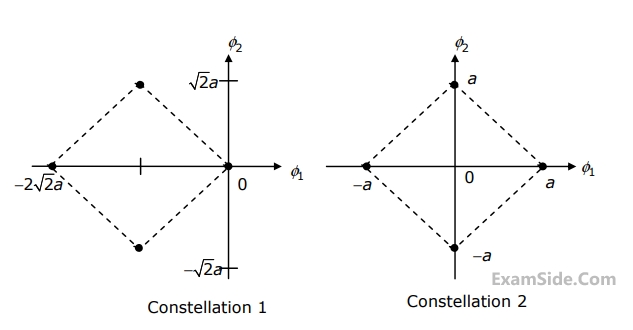
The ratio of the average energy of Constellation 1 to the average energy of Constellation 2 is

If these constellations are used for digital communications over an AWGN channel, then which of the following statements is true?
The impulse response of filter matched to the signal $$s(t) = g(t)$$ $$ - \delta {\left( {t - 2} \right)^ * }\,\,g\left( t \right)$$ is given as:

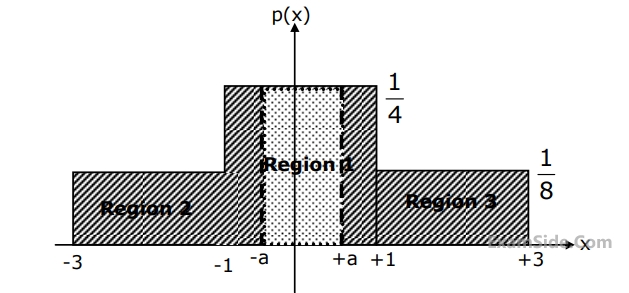
The quantization noise power for the quantization region between –a and +a in the figure is
If the input probability density function is divided into three regions as shown in figure, the value of 'a' in the figure is
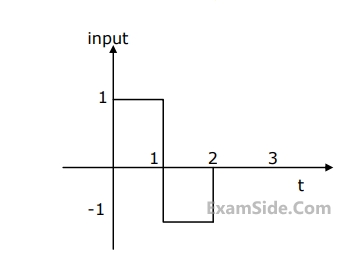
The peak amplitude of the filter output is