Maxwell Equations · Electromagnetics · GATE ECE

Marks 1

Let $\hat{i}$ and $\hat{j}$ be the unit vectors along $x$ and $y$ axes, respectively and let $A$ be a positive constant. Which one of the following statements is true for the vector fields $\vec{F}_1 = A(\hat{i}y + \hat{j}x)$ and $\vec{F}_2 = A(\hat{i}y − \hat{j}x)$?

GATE ECE 2024

In a circuit, there is a series connection of an ideal resistor and an ideal capacitor. The conduction current (in Amperes) through the resistor is 2sin(t + $$\pi$$/2). The displacement current (in Amperes) through the capacitor is __________.

GATE ECE 2022

Two conducting spheres S1 and S2 of radii a and b (b>a) respectively, are placed far apart and connected by a long, thin conducting wire, as shown in the figure.

For some charge placed on this structure, the potential and surface electric field on S1 are V_a and E_a , and that on S2 are V_b and E_b, respectively, which of the following is CORRECT?

GATE ECE 2017 Set 2

A uniform and constant magnetic field $$B=\widehat zB$$ exists in the $$\widehat z$$ direction in vacuum. A particle of mass m with a small charge q is introduced into this region with an initial velocity $$v=\widehat xv_x+\widehat zv_z$$. Given that B, m, q, v_x and v_z are all non-zero, which one of the following describes the eventual trajectory of the particle?

GATE ECE 2016 Set 2

Consider the time-varying vector $$I = \,\hat x\,\,15\,\cos \,(\omega \,t) + \,\hat y\,5\,sin(\omega \,t)$$ in Cartesian coordinates, where $$\omega $$ > 0 is a constant. When the vector magnitude $$\left| I \right|$$ is at its minimum value, the angle $$\theta $$ that I makes with the x axis (in degree, such that $$0\, \le \,0 \le \,180$$) is _________________

GATE ECE 2016 Set 2

Concentric spherical shells of radii 2 m, 4 m, and 8 m carry uniform surface charge densities of 20 nC/m² , −4 nC/m² and ρ_s ,respectively. The value of ρ_s (nC/m²) required to ensure that the electric flux density $$\overrightarrow D=\overrightarrow0$$ at radius 10 m is _________.

GATE ECE 2016 Set 1

Faraday's law of electromagnetic induction is mathematically described by which one of the following equations?

GATE ECE 2016 Set 3

In a source free region in vacuum, if the electrostatic potential $$\varphi\;=\;2x^2\;+y^2+cz^2$$ , the value of constant c must be ________________.

GATE ECE 2015 Set 2

The divergence of the vector field $$\overrightarrow A\;=\;x{\widehat a}_x\;+\;y{\widehat a}_y\;+\;z{\widehat a}_z$$ is

GATE ECE 2013

Consider a closed surface S surrounding volume V. If $$\overrightarrow{\mathrm r}$$ is the position vector of a point inside S, with $$\widehat n$$ the unit normal on S, the value of the integral is

GATE ECE 2011

Two infinitely long wires carrying current are as shown in the figure below. One wire is in the y-z plane and parallel to the y-axis. The other wire is in the x-y plane and parallel to the x-axis. Which components of the resulting magnetic field are non-zero at the origin?

GATE ECE 2009

If C is a closed curve enclosing a surface S, then the magnetic field intensity $$\overrightarrow H $$, the current density $$\overrightarrow J $$ and the electric flux density $$\overrightarrow D $$ are related by

GATE ECE 2007

$$\nabla \times \nabla \times P$$, where P is a vector, is equal to

GATE ECE 2006

$$\int\int\left(\nabla\times\mathrm P\right)\;\cdot\mathrm{ds}$$ , where is a vector, is equal to

GATE ECE 2006

The unit of $$\nabla\times\mathrm H$$ is

GATE ECE 2003

Identify which one of the following will NOT satisfy the wave equation.

GATE ECE 1999

An electric field on a plane is described by its potential V = $$20\left(r^{-1}\;+\;r^{-2}\right)$$ where r is the distance from the source. The field is due to

GATE ECE 1999

The Maxwell's equation $$\nabla\times\overrightarrow H\;=\;\overrightarrow J\;+\;\frac{\partial\overrightarrow D}{\partial t}$$ is based on

GATE ECE 1998

A loop is rotating about the y-axis in a magnetic field $$$\overrightarrow B\;=\;B_0\cos\left(\mathrm{ωt}\;+\;\mathrm\phi\;\right)\;{\overrightarrow a}_x\;\mathrm T .$$$ The voltage in the loop is

GATE ECE 1998

The time averaged Poynting vector, in W/m², for a wave with $$\vec E = 24{e^{j\left( {\omega t + \beta z} \right)}}{\mkern 1mu} {\overrightarrow a _y}$$ V/m in free space is

GATE ECE 1998

A metal sphere with 1 m radius and a surface charge density of 10 Coulombs/m² is enclosed in a cube of 10 m side. The total outward electric displacement normal to the surface of the cube is

GATE ECE 1996

The electric field strength at a distance point, P, due to a point charge, +q, located at the origin, is 100 $$\mu $$V/m. If the point charge is now enclosed by a perfectly conducting metal sheet sphere whose center is at the origin, then the electric field strength at the point P outside the sphere becomes.

GATE ECE 1995

In the infinite plane, y = 6 m, there exists a uniform surface charge density of (1/6000$$\pi $$) $$\mu $$C/m². The associated electric field strength is:

GATE ECE 1995

GATE ECE 1994

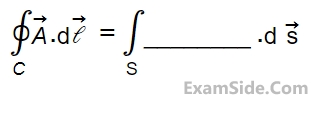
Marks 2

In an electrostatic field, the electric displacement density vector, $$\overrightarrow D $$, is given by

$$\overrightarrow D (x,y,z) = ({x^3}\overrightarrow i + {y^3}\overrightarrow j + x{y^2}\overrightarrow k )$$ C/m²,

where, $$\overrightarrow i $$, $$\overrightarrow j $$, $$\overrightarrow k $$ are the unit vectors along x-axis, y-axis, and z-axis, respectively. Consider a cubical region R centered at the origin with each side of length 1 m, and vertices at ($$\pm$$ 0.5 m, $$\pm$$ 0.5 m, $$\pm$$ 0.5 m). The electric charge enclosed within R is __________ C (rounded off to two decimal places).

GATE ECE 2022

An electron (q₁) is moving in free space with velocity 10⁵ m/s towards a stationary electron (q₂) far away. The closest distance that this moving electron gets to the stationary electron before the repulsive force diverts its path is ___________ ×10^-8m.

[Given, mass of electron m = 9.11×10^-31 kg, charge of electron e = -1.6×10^-19 C , and permittivity $$\varepsilon_0=\left(1/36\mathrm\pi\right)\times10^{-9}\;\mathrm F/\mathrm m$$].

GATE ECE 2017 Set 2

The parallel-plate capacitor shown in the figure has movable plates. The capacitor is charged so that the energy stored in it is E when the plate separation is d. The capacitor is then isolated electrically and the plates are moved such that the plate separation becomes 2d.

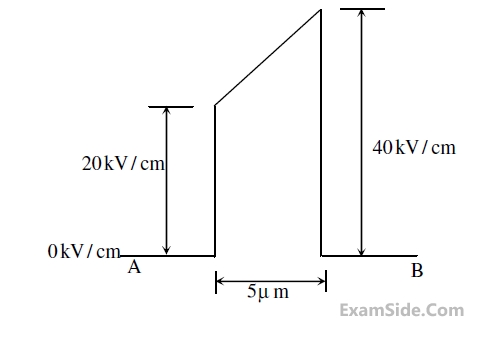
At this new plate separation, what is the energy stored in the capacitor, neglecting fringing effects?

GATE ECE 2016 Set 2

A coaxial capacitor of inner radius 1 mm and outer radius 5 mm has a capacitance per unit length of 172 pF/m. If the ratio of outer radius to inner is doubled, the capacitance per unit length (in pF/m) is _____.

GATE ECE 2015 Set 3

The electric field (assumed to be one-dimensional) between two points A and B is shown. Let $$\psi_A$$ and $$\psi_B$$ be the electrostatic potentials at A and B, respectively. The value of $$\psi_A$$ − $$\psi_B$$ in Volts is ________.

GATE ECE 2014 Set 4

If $$\overrightarrow{\mathrm E}=-\left(2\mathrm y^2\;-3\mathrm{yz}^2\right)\widehat{\mathrm x}\;-\left(6\mathrm{xy}^2-3\mathrm{xz}^2\right)\widehat{\mathrm y}+\left(6\mathrm{xyz}\right)\widehat{\mathrm z}$$

is the electric field in a source free region, a valid expression for the electrostatic potential is

GATE ECE 2014 Set 4

Given the vector $$$\mathrm A=\left(\cos\;\mathrm x\right)\left(\sin\;\mathrm y\right)\;{\widehat{\mathrm a}}_\mathrm x\;+\;\left(\sin\;\mathrm x\right)\left(\cos\;\mathrm y\right){\widehat{\mathrm a}}_\mathrm y$$$ where $${\widehat{\mathrm a}}_\mathrm x$$ , $${\widehat{\mathrm a}}_\mathrm y$$ denote unit vectors along x, y directions, respectively. The magnitude of curl of A is ________

GATE ECE 2014 Set 3

An infinitely long uniform solid wire of radius a carries a uniform dc current of density $$\widehat{\mathrm j}$$.

A hole of radius b (b < a) is now drilled along the length of the wire at a distance d from the center of the wire as shown below.

The magnetic field inside the hole is

GATE ECE 2012

An infinitely long uniform solid wire of radius a carries a uniform dc current of density $$\widehat{\mathrm j}$$

The magnetic field at a distance r from the center of the wire is proportional to

GATE ECE 2012

If $$\overrightarrow{\mathrm A}\;=\;\mathrm{xy}\;{\widehat{\mathrm a}}_\mathrm x\;+\;\mathrm x^2\;{\widehat{\mathrm a}}_\mathrm y$$ then $$\oint\overrightarrow{\mathrm A}.\overrightarrow{\mathrm d}\mathcal l$$ over the path shown in the figure is

GATE ECE 2010

The value of the integral of the function $$\mathrm g\left(\mathrm x,\mathrm y\right)=4\mathrm x^3\;+\;10\mathrm y^4$$ along the straight line segment from the point (0, 0) to the point (1, 2) in the x-y plane is

GATE ECE 2008

If the electric field intensity is given by $$\mathrm E=\left(\mathrm x{\widehat{\mathrm u}}_\mathrm x\;+\mathrm y{\widehat{\mathrm u}}_\mathrm y+\mathrm z{\widehat{\mathrm u}}_\mathrm z\right)\;\mathrm{volt}/\mathrm m$$, the potential difference between X(2,0,0) and Y(1,2,3) is

GATE ECE 2003

A material has conductivity of 10^-2 mho/m and a relative permittivity of 4. The frequency at which the conduction current in the medium is equal to the displacement current is

GATE ECE 2001

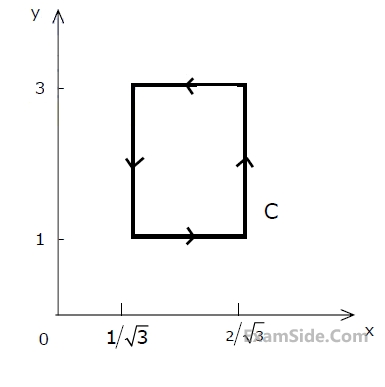
Given,$$\overrightarrow V=x\cos^2y\;\;\widehat{\mathrm i}\;+\;\mathrm x^2\mathrm e^\mathrm z\;\widehat{\mathrm j}\;+\;\mathrm{zsin}^2\mathrm y\;\widehat{\mathrm k}$$ and S the surface of a unit cube with one corner at the origin and edges parallel to the coordinate axes, the value of the integral is

GATE ECE 1993

Which of the following field equations indicate that the free magnetic charges do not exits?

GATE ECE 1990

The incoming solar radiation at a place on the surface of the earth is 1.2 KW/m².The amplitude of the electric field corresponding to this incident power is nearly equal to

GATE ECE 1990

The electric field strength at a far-off point P due to a point charge + q, located at the origin O is 100 millivolts/metre. The point charge is now enclosed by a perfectly conducting hollow metal sphere with its centre at the origin O. The electric field strength at the point, P,

GATE ECE 1989

Vector potential is a vector

GATE ECE 1988

On either side of a charge-free interface between two media,

GATE ECE 1988

An electrostatic field is said to be conservative when

GATE ECE 1987

Two long parallel wires in free space are separated by a distance R and carry currents of equal magnitude but opposite in direction. At any general point, the Z-component of

GATE ECE 1987