1
GATE ME 2008
MCQ (Single Correct Answer)
+2
-0.6
For the network below, the objective is to find the length of the shortest path from node $$P$$ to node $$G.$$ Let $${d_{ij}}$$ be the length of directed are from node $$i$$ to node $$j$$. Let $${s_j}$$ be the length of the shortest path from $$P$$ to node $$j.$$ Which of the following equations can be used to find $${s_G}$$?
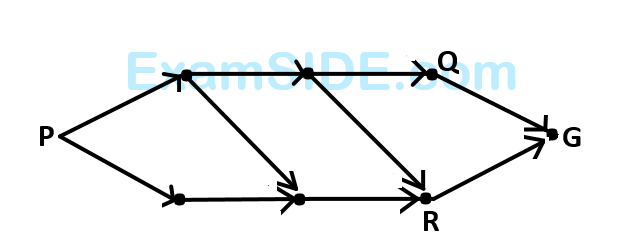

2
GATE ME 2006
MCQ (Single Correct Answer)
+2
-0.6
Consider a $$PERT$$ network for a project involving six tasks ($$a$$ to $$f$$)
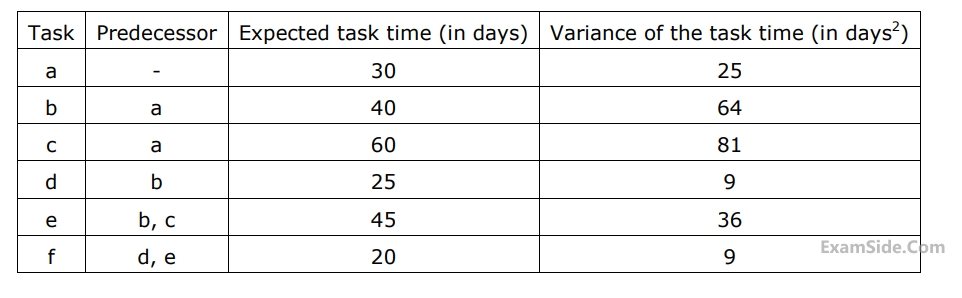

The expected completion time of the project is
3
GATE ME 2006
MCQ (Single Correct Answer)
+2
-0.6
Consider a $$PERT$$ network for a project involving six tasks ($$a$$ to $$f$$)


The standard deviation of the critical path of the project is
4
GATE ME 2005
MCQ (Single Correct Answer)
+2
-0.6
A project has six activities $$(A$$ to $$F)$$ with respective activity durations $$7,5,6,6,8,4$$ days. The network has three paths $$A-B,C-D$$ and $$E-F.$$ All the activities can be crashed with the same crash cost per day. The number of activities that need to be crashed to reduce the project duration by $$1$$ day is
Questions Asked from Pert and Cpm (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ME 2025 (1)
GATE ME 2022 Set 2 (1)
GATE ME 2022 Set 1 (1)
GATE ME 2017 Set 2 (1)
GATE ME 2016 Set 2 (1)
GATE ME 2015 Set 2 (1)
GATE ME 2015 Set 1 (1)
GATE ME 2014 Set 4 (1)
GATE ME 2014 Set 3 (1)
GATE ME 2014 Set 2 (1)
GATE ME 2012 (2)
GATE ME 2010 (1)
GATE ME 2009 (2)
GATE ME 2008 (1)
GATE ME 2006 (2)
GATE ME 2005 (1)
GATE ME 2003 (1)
GATE ME 2002 (1)
GATE ME 1990 (1)
GATE ME Subjects
Engineering Mechanics
Machine Design
Strength of Materials
Heat Transfer
Production Engineering
Industrial Engineering
Turbo Machinery
Theory of Machines
Engineering Mathematics
Fluid Mechanics
Thermodynamics
General Aptitude