Fluid Kinematics · Fluid Mechanics · GATE ME
Marks 1
1
The velocity field of a two-dimensional, incompressible flow is given by $\overrightarrow{V} = \ 2sin{h}\,x\,\hat{i} + v(x,y)\hat{j}$ where $ \hat{i}$ and $\underset{\dot{}}{j}$ denote the unit vectors in x and y directions, respectively. If $v(x, 0) = cosh\ x$, then $v(0,-1)$ is
GATE ME 2024
2
The velocity field in a fluid is given to be $\vec{V}=(4xy)\hat{i}+2(x^2-y^2)\hat{j}$ Which of the following statement(s) is/are correct?
GATE ME 2022 Set 2
3
A tiny temperature probe is fully immersed in a flowing fluid and is moving with zero relative velocity with respect to the fluid. The velocity field in the fluid is $\vec V = (2x) \hat i + (y + 3t) \hat j,$ and the temperature field in the fluid is T = 2x2 + xy + 4t, where x and y are the spatial coordinates, and t is the time. The time rate of change of temperature recorded by the probe at (x = 1, y = 1, t = 1) is _______.
GATE ME 2022 Set 1
4
Consider the two-dimensional velocity field given by
$$\overrightarrow V = \left( {5 + {a_1}x + {b_1}y} \right)\widehat i + \left( {4 + {a_2}x + {b_2}y} \right)\widehat j,$$
where $${a_1},\,\,{b_1},\,\,{a_2}$$ and $${b^2}$$ are constants. Which one of the following conditions needs to be satisfied for the flow to be incompressible?
$$\overrightarrow V = \left( {5 + {a_1}x + {b_1}y} \right)\widehat i + \left( {4 + {a_2}x + {b_2}y} \right)\widehat j,$$
where $${a_1},\,\,{b_1},\,\,{a_2}$$ and $${b^2}$$ are constants. Which one of the following conditions needs to be satisfied for the flow to be incompressible?
GATE ME 2017 Set 1
5
The volume tric flow rate (per unit depth) between two streamlines having stream functions $${\psi _1}$$ & $${\psi _2}$$ is
GATE ME 2016 Set 2
6
A channel of width $$450$$ $$mm$$ branches into two sub-channels having width $$300$$ $$mm$$ and $$200$$ $$mm$$ as shown in figure. If the volumetric flow rate (taking unit depth) of an incompressible flow through the main channel is $$0.9$$ $$3$$ $$m/s,$$ and the velocity in the sub-channel of width $$200$$ $$mm$$ is $$3$$ $$m/s,$$ the
velocity in the sub-channel of width $$300$$ $$mm$$ is _____________ $$m/s$$.
Assume both inlet and outlet to be at the same elevation.
GATE ME 2016 Set 3
7
For a certain two-dimensional incompressible flow, velocity field is given by $$2xy\widehat i - {y^2}\widehat j.$$ The streamlines for this flow are given by the family of curves
GATE ME 2016 Set 3
8
If the fluid velocity for a potential flow is given by $$V\left( {x,y} \right) = u\left( {x,y} \right)i + v\left( {x,y} \right)j$$ with usual notations, then the slope of potential line at $$(x, y)$$ is
GATE ME 2015 Set 2
9
A flow field which has only convective acceleration is
GATE ME 2014 Set 4
10
A flow field which has only convective acceleration is
GATE ME 2014 Set 4
11
For an incompressible flow field , $$\overrightarrow {V,} $$ which one of the following conditions must be satisfied?
GATE ME 2014 Set 2
12
A streamline and an equipotential line in a flow field
GATE ME 2011
13
For a continuity equation given $$\nabla .\overrightarrow V = 0$$ to be valid, $$\overrightarrow V $$ where is the velocity vector, which one of the folllowing is a necessary condition ?
GATE ME 2008
14
In a steady flow through a nozzle, the flow velocity on the nozzle axis is given by $$u = {u_0}\left( {1 + 3x/L} \right),\,\,$$ where $$x$$ is the distance along the axis of the nozzle from its inlet plane and $$L$$ is the length of the nozzle. The time required for a fluid particle on the axis to travel from the inlet to the exit plane of the nozzle is .
GATE ME 2007
15
In a two-dimensional velocity field with velocities $$u$$ and $$v$$ along $$x$$ and $$y$$ directions respectively, the convective acceleration along the $$x$$-direction is given by
GATE ME 2006
16
A two-dimensional flow field has velocities along the $$x$$ and $$y$$ directions given by $$u = {x^2}t$$ and $$v = - 2xyt$$ respectively, where $$t$$ is time. The equation of streamline is
GATE ME 2006
17
The velocity components in the $$x$$ and $$y$$ directions of a two dimensional potential flow are $$u$$ and $$v$$, respectively. Then $${{\partial u} \over {\partial y}}$$ is equal to
GATE ME 2005
18
A fluid flow is represented by the velocity field $$\overrightarrow V = ax\,\overrightarrow i + ay\,\overrightarrow j ,$$ where a constant . The equation of stream line passing through a point $$(1, 2)$$ is
GATE ME 2004
19
In a flow field, the streamlines and equipotential lines
GATE ME 1994
20
Existence of velocity potential implies that
GATE ME 1994
21
Streamlines, path lines and streak lines are virtually identical for
GATE ME 1994
22
For a fluid element in a two dimensional flow field ($$x-y$$ plane), it will undergo
GATE ME 1994
23
Circulation is defined as line integral of tangential component of velocity about a _________ (fill in the blank)
GATE ME 1994
Marks 2
1
A steady two-dimensional flow field is specified by the stream function
ψ = kx3y,
where x and y are in meters and the constant k = 1 m-2s-1. The magnitude of acceleration at a point (x, y) = (1 m, 1 m) is ________ m/s2 (round off to 2 decimal places).
GATE ME 2022 Set 1
2
For a steady flow, the velocity field is $$\overrightarrow V = \left( { - {x^2} + 3y} \right)\widehat i + \left( {2xy} \right)\widehat j.$$ The magnitude of the acceleration of the particle at $$(1, -1)$$ is
GATE ME 2017 Set 1
3
For a two-dimensional flow, the velocity field is $$\overrightarrow u = {x \over {{x^2} + {y^2}}}\widehat i + {y \over {{x^2} + {y^2}}}\widehat j,$$ where $$\widehat i$$ and $$\widehat j\,\,$$ are the basis vectors in the $$x$$-$$y$$ Cartesian coordinate system .
Identify the CORRECT statements from below.
(1) The flow is incompressible
(2) The flow is unsteady
(3) $$y$$-component of acceleration, $${a_y} = {{ - y} \over {{{\left( {{x^2} + {y^2}} \right)}^2}}}$$
(4) $$x$$-component of acceleration , $${a_x} = {{ - \left( {x + y} \right)} \over {{{\left( {{x^2} + {y^2}} \right)}^2}}}$$
Identify the CORRECT statements from below.
(1) The flow is incompressible
(2) The flow is unsteady
(3) $$y$$-component of acceleration, $${a_y} = {{ - y} \over {{{\left( {{x^2} + {y^2}} \right)}^2}}}$$
(4) $$x$$-component of acceleration , $${a_x} = {{ - \left( {x + y} \right)} \over {{{\left( {{x^2} + {y^2}} \right)}^2}}}$$
GATE ME 2016 Set 3
4
Match the following pairs:
GATE ME 2015 Set 1
5
The velocity field on an incompressible flow is given by
$$V = \left( {{a_1}x + {a_2}y + {a_3}z} \right)i + \left( {{b_1}x + {b_2}y + {b_3}z} \right)j$$ $$$ + \left( {{c_1}x + {c_2}y + {c_3}z} \right)k,$$$
$$V = \left( {{a_1}x + {a_2}y + {a_3}z} \right)i + \left( {{b_1}x + {b_2}y + {b_3}z} \right)j$$ $$$ + \left( {{c_1}x + {c_2}y + {c_3}z} \right)k,$$$
Where $${a_1} = 2$$ and $${c_3} = - 4.$$ The value of $${b_2}$$ is _____________.
GATE ME 2015 Set 1
6
Consider the following statements regarding streamline(s):
(i) It is a continuous line such that the tangent at any point on it shows the velocity vector at that point
(ii) There is no flow across streamlines
(iii) $${{dx} \over u} = {{dy} \over v} = {{dz} \over w}$$ is the differential equation of a streamline, where $$u,v$$ and $$w$$ are velocities in directions $$x,y$$ and $$z,$$ respectively
In an unsteady flow, the path of a particle is a streamline
(i) It is a continuous line such that the tangent at any point on it shows the velocity vector at that point
(ii) There is no flow across streamlines
(iii) $${{dx} \over u} = {{dy} \over v} = {{dz} \over w}$$ is the differential equation of a streamline, where $$u,v$$ and $$w$$ are velocities in directions $$x,y$$ and $$z,$$ respectively
In an unsteady flow, the path of a particle is a streamline
Which one of the following combinations of the statements is true?
GATE ME 2014 Set 4
7
Consider a velocity field $$\overrightarrow V = K\left( {y\widehat i + x\widehat k} \right),$$ where $$K$$ is a constant. The vorticity, $${\Omega _z},$$ is
GATE ME 2014 Set 4
8
Velocity vector of a flow fields is given as $$\overrightarrow V = 2xy\widehat i - {x^2}z\widehat j.$$ The vorticity vector at $$(1,1,1)$$ is
GATE ME 2010
9
You are asked to evaluate assorted fluid flows for their suitability in a given laboratory application. The following three flow choices. Expressed in terms of the two - dimensional velocity fields in the $$x-$$ $$y$$ plane, are made available.
$$P:$$ $$u = 2y,\,\,\,v = - 3x$$
$$Q:$$ $$u=3xy,$$ $$\,\,\,\,$$$$v=0$$
$$R:$$ $$u=-2x,$$ $$\,\,\,\,$$$$v=2y$$
$$P:$$ $$u = 2y,\,\,\,v = - 3x$$
$$Q:$$ $$u=3xy,$$ $$\,\,\,\,$$$$v=0$$
$$R:$$ $$u=-2x,$$ $$\,\,\,\,$$$$v=2y$$
Which flows should be recommended when the application requires the flow to be incompressible and irrotational?
GATE ME 2009
10
The gap between a moving circular plate and a stationary surface is being continuously reduced, as the circular plate comes down at a uniform speed $$V$$ towards the stationary bottom surface, as shown in the figure. In the process, the fluid contained between the two plates flows out radially. The fluid is assumed to be incompressible and inviscid.
The radial velocity $${V_r},$$ at any radius $$r$$, when the gap width is $$h,$$ is
GATE ME 2008
11
The gap between a moving circular plate and a stationary surface is being continuously reduced, as the circular plate comes down at a uniform speed $$V$$ towards the stationary bottom surface, as shown in the figure. In the process, the fluid contained between the two plates flows out radially. The fluid is assumed to be incompressible and inviscid.
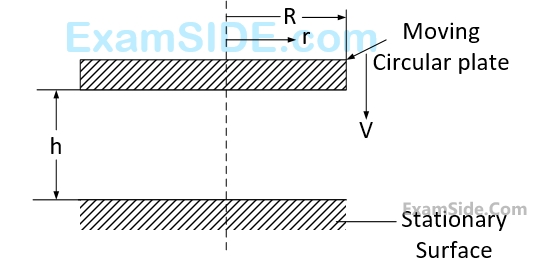
The radial component of the fluid acceleration at $$r=R$$ is
GATE ME 2008
12
Which combination of the following statements about steady incompressible forced vortex flow is correct?
P: Shear stress is zero at all points in the flow.
Q: Velocity is directly proportional to the radius from the centre of the vortex.
R: Total mechanical energy per unit mass is constant in the entire flow field.
S: Total mechanical energy per unit mass is constant in the entire flow field.
GATE ME 2007
13
A leaf is caught in a whirlpool. At a given instant, the leaf is at a distance of $$120$$ $$m$$ from the centre of the whirlpool. The whirlpool can be described by the following velocitry distribution ;
$${V_r} = - \left( {{{60 \times {{10}^3}} \over {2\pi r}}} \right)m/s$$
and $${V_\theta } = - \left( {{{300 \times {{10}^3}} \over {2\pi r}}} \right)m/s.$$
$${V_r} = - \left( {{{60 \times {{10}^3}} \over {2\pi r}}} \right)m/s$$
and $${V_\theta } = - \left( {{{300 \times {{10}^3}} \over {2\pi r}}} \right)m/s.$$
Where $$r$$ (in meters) is the distance from the centre of the whirlpool . What will be the distance of the leaf from the centre when it has moved through half a revolution?
GATE ME 2005
14
For a fluid flow through a divergent pipe of length $$L$$ having inlet and outlet radii of $${R_1}$$ and $${R_2}$$ respectively and a constant flow rate of $$Q,$$ assuming the velocity to be axial and uniform at any cross- section , the acceleration at the exit is
GATE ME 2004
15
A closed cylinder having a radius $$R$$ and height $$H$$ is filled with oil of density $$\rho .$$ If the cylinder is rotated about its axis at an angular velocity of $$\omega $$ , then thrust at the bottom of the cylinder is
GATE ME 2004
16
The $$2$$ - $$D$$ flow with, velocity $$\overrightarrow v = \left( {x + 2y + 2} \right)\overrightarrow i + \left( {4 - y} \right)\overrightarrow j $$ is
GATE ME 2001
17
The velocity components in the $$x$$ and $$y$$ directions are given by $$u = \lambda x{y^3} - {x^2}y,$$ $$v = x{y^2} - {3 \over 4}{y^4}.$$ The value of $$\lambda $$ for a possible flow field involving an incompressible fluid is
GATE ME 1995
18
A velocity field is given as
$$$\overrightarrow V = 3{x^2}y\widehat i - 6xyz\widehat k$$$
Where $$x,y,z$$ are in $$m$$ and $$V$$ $$m/s.$$ Determine if
Where $$x,y,z$$ are in $$m$$ and $$V$$ $$m/s.$$ Determine if
(i) It represents an incompressible flow
(ii) The flow is irrotational
(iii) The flow is steady .
GATE ME 1993
19
The stream function in a two dimensional flow field is given by $$\Psi = {x^2} - {y^2}$$
The magnitude of the velocity at point $$(1,1)$$ is
The magnitude of the velocity at point $$(1,1)$$ is
GATE ME 1989
20
A Newtonian fluid has the following velocity field :
$$$\overrightarrow V = {x^2}y\widehat i + 2x{y^2}z\widehat j - y{z^3}\widehat k$$$
The rate of shear deformation $${\varepsilon _{yz}}$$ at the point $$x=-2, y=-1$$ and $$z=2$$ for the given flow is :
GATE ME 1988