Turbo Machinery · Turbo Machinery · GATE ME

Marks 1

Which one of the following statement is TRUE?

GATE ME 2017 Set 2

Which one of the following is NOT a rotating machine?

GATE ME 2017 Set 1

The blade and fluid velocities for an axial turbine are as shown in the figure.

The magnitude of absolute velocity at entry is $$300$$ $$m/s$$ at an angle of $${65^0}$$ to the axial direction, while the magnitude of the absolute velocity at exit is $$150$$ $$m/s.$$ The exit velocity vector has a component in the downward direction. Given that the axial (horizontal) velocity is the same at entry and exit, the specific work (in $$kJ/kg$$) is ______________.

GATE ME 2016 Set 3

Consider two hydraulic turbines having identical specific speed and effective head at the inlet. If the speed ratio $$\left( {{{{N_1}} \over {{N_2}}}} \right)$$ of the two turbines is $$2,$$ then the respective power ratio $$\left( {{{{P_1}} \over {{P_2}}}} \right)$$ is _______________________.

GATE ME 2016 Set 1

Kaplan water turbine is commonly used when the flow through its runner is

GATE ME 2014 Set 4

In order to have maximum power from a Pelton turbine, the bucket speed must be

GATE ME 2013

A phenomenon is modeled using $$n$$ dimensional variables with $$k$$ primary dimensions. The number of non-dimensional variables is

GATE ME 2010

A hydraulic turbine develops $$1000$$ $$kW$$ power for a head of $$40$$ $$m.$$ If the head is reduced to $$20$$ $$m,$$ the power developed (in $$kW$$) is

GATE ME 2010

A model of a hydraulic turbine is tested at a head of $$1/{4^{th}}$$ of that under which the full scale turbine works. The diameter of the model is half of that of the full scale turbine. If $$N$$ is the $$RPM$$ of the full scale turbine, then the $$RPM$$ of the model will be

GATE ME 2007

The inlet angle of runner blades of a Francis turbine is $${90^0}.$$ The blades are so shaped that the tangential component of velocity at blade outlet is zero. The flow velocity remains constant throughout the blade passage and is equal to half of the blade velocity at runner inlet. The blade efficiency of the runner is

GATE ME 2007

Match the items in columns $$I$$ and $$II$$.

Column $$I$$
$$P:$$ Centrifugal compressor
$$Q:$$ Centrifugal pump
$$R:$$ Pelton wheel
$$S:$$ Kaplan turbine

Column $$II$$
$$1:$$ Axial flow
$$2:$$ Surging
$$3:$$ Priming
$$4:$$ Pure impulse

GATE ME 2007

A large hydraulic turbine is to generate $$300$$ $$kW$$ at $$1000$$ $$rpm$$ under a head of $$40$$ $$m$$. for initial testing, a $$1:4$$ scale model of the turbine operates under a head of $$10$$ $$m.$$ the power generated by the model (in $$kW$$) will be

GATE ME 2006

A horizontal shaft centrifugal pump lifts ware at 65°C. The suction nozzle is one meter below pump centerline. The pressure at this point equal $$200$$ $$kPa$$ gauge and velocity is $$3$$ $$m/s.$$ Steam tables show saturation pressure at $${65^0}C$$ is $$25$$ $$kPa,$$ and specific volume of the saturated liquid is $$0.001020$$$ $${m^3}/kg.$$ . The pump Net Positive suction Head ($$NPSH$$) in meters is

GATE ME 2006

In a Pelton wheel, the bucket peripheral speed is $$10$$ $$m/s,$$ the water jet velocity is $$25$$ $$m/s$$ and volumetric flow rate of the jet is $$0.1{m^3}/s.$$ If the jet deflection angle is $${120^0}$$ and the flow is ideal, the owe developed is:

GATE ME 2006

At a hydro electric power plant site, available head and flow rate are $$24.5$$ $$m$$ and $$10.1{m^3}/s$$ respectively. If the turbine to be installed is required to run at $$4.0$$ revolution per second ($$rps$$) with an overall efficiency of $$90\% $$, the suitable type of turbine for this site is _______________.

GATE ME 2004

A centrifugal pump is required to pump water to an open water tank situated $$4$$ $$km$$ away from the location of the pump through a pipe of diameter $$0.2$$ $$m$$ having Darcy’s friction factor of $$0.01.$$ The average speed of water in the pipe is $$2$$ $$m/s.$$ if it is maintain a constant head of $$5$$ $$m$$ in the tank, neglecting other minor losses, the absolute discharge pressure at the pump exist is ______________

GATE ME 2004

If there are $$'m'$$ physical quantities and $$'n'$$ fundamental dimensions in a particular process, the number of non-dimensional parameters is

GATE ME 2002

Kaplan turbine is

GATE ME 1997

In terms of speed of rotation of the impeller $$N$$, discharge $$Q$$ and a change in total head $$H$$, through the machine,the Specific Speed for a pump is ________________ (fill the blank)

GATE ME 1994

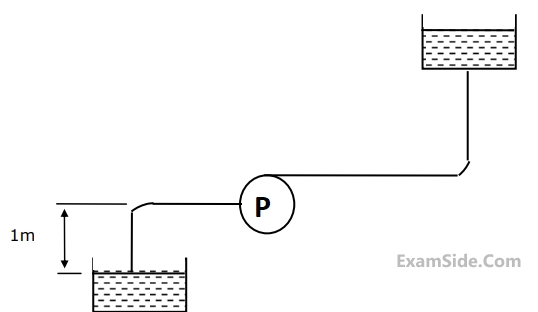
Marks 2

Consider a Pelton wheel of 1 m diameter. The magnitude of relative velocity of water at the bucket inlet is same as the magnitude of relative velocity of water at the bucket exit. The absolute speed of water at the bucket inlet is $125.66 \mathrm{~m} \mathrm{~s}-1$. For maximum power output from the Pelton wheel, the rpm of the Pelton wheel is_______ (rounded off to 1 decimal place).

GATE ME 2025

Consider an air-standard Brayton cycle with adiabatic compressor and turbine, and a regenerator, as shown in the figure. Air enters the compressor at 100 kPa and 300 K and exits the compressor at 600 kPa and 550 K. The air exits the combustion chamber at 1250 K and exits the adiabatic turbine at 100 kPa and 800 K. The exhaust air from the turbine is used to preheat the air in the regenerator. The exhaust air exits the regenerator (state 6) at 600 K. There is no pressure drop across the regenerator and the combustion chamber. Also, there is no heat loss from the regenerator to the surroundings. The ratio of specific heats at constant pressure and volume is $c_p/c_v$= 1.4. The thermal efficiency of the cycle is ________% (answer in integer).