Metal Cutting · Production Engineering · GATE ME
Marks 1
1
The grinding wheel used to provide the best surface finish is
GATE ME 2024
2
In an orthogonal cutting process the tool used has rake angle of zero degree. The measured cutting force and thrust force are $$500$$ $$N$$ and $$250$$ $$N,$$ respectively. The coefficient of friction between the tool and the chip is ________________
GATE ME 2016 Set 1
3
Under certain cutting conditions, doubling the cutting speed reduces the tool life to $${\left( {{1 \over {16}}} \right)^{th}}$$ of the original. Taylor’s tool life index $$(n)$$ for this tool workpiece combination will be ______________
GATE ME 2015 Set 1
4
Better surface finish is obtained with a large rake angle because
GATE ME 2014 Set 4
5
If the Taylor's tool life exponent $$n$$ is $$0.2,$$ and the tool changing time is $$1.5$$ $$min,$$ then the tool life (in min) for maximum production rate is ____________
GATE ME 2014 Set 1
6
The main cutting force acting on a tool during the turning (orthogonal cutting) operation of a metal is $$400N.$$ The turning was performed using $$2mm$$ depth of cut and $$0.1mm/rev$$ feed rate. The specific cutting pressure (in $$N/m{m^2}$$ is
GATE ME 2014 Set 1
7
A straight turning operation is carried out using a single point cutting tool on an $$AISI$$ $$1020$$ steel rod. The feed is $$0.2$$ $$mm/rev$$ and the depth of cut is $$0.5$$ $$mm.$$ The tool has a side cutting edge angle of $${60^ \circ }.$$ The uncut chip thickness (in $$mm$$) is _______________
GATE ME 2014 Set 3
8
Cutting tool is much harder than the work piece. Yet the tool wears out during the tool-work interaction, because
GATE ME 2014 Set 3
9
Friction at the tool - chip interface can be reduced by
GATE ME 2009
10
The minimum shear strain in orthogonal turning with a cutting tool of zero rake angle is
GATE ME 2009
11
Formation on build-up edge during machining can be avoided by using
GATE ME 2003
12
$$BUE$$ is formed while machining
GATE ME 2002
13
A built up edge is formed while machining
GATE ME 2000
14
Cutting power consumption in turning can be signification reduced by
GATE ME 1995
15
The effect of rake angle on the mean friction angle in machining can be explained by
GATE ME 1992
16
Most of the metal cutting heat goes into the
GATE ME 1991
17
Most of the metal cutting heat goes into the
GATE ME 1990
18
The size of $$BLUE$$ in metal cutting increases with
GATE ME 1989
19
Crater wear always starts at some distance from the tool tip because at that point
GATE ME 1989
20
The ideal cutting fluid for low speed machining of metals should be one which
GATE ME 1988
21
If in a turning operation both the feed rate and the nose radius are doubled the surface finish values will be
GATE ME 1987
22
Cutting tools are provided with large positive rake angle mainly for
GATE ME 1987
Marks 2
1
A cutting tool provides a tool life of 60 minutes while machining with the cutting speed of 60 m/min. When the same tool is used for machining the same material, it provides a tool life of 10 minutes for a cutting speed of 100 m/min. If the cutting speed is changed to 80 m/min for the same tool and work material combination, the tool life computed using Taylor’s tool life model is _______ minutes (rounded off to 2 decimal places).
GATE ME 2024
2
In an ideal orthogonal cutting experiment (see figure), the cutting speed V is 1 m/s, the rake angle of the tool α = 5°, and the shear angle, 𝜙, is known to be 45°.
Applying the ideal orthogonal cutting model, consider two shear planes PQ and RS close to each other. As they approach the thin shear zone (shown as a thick line in the figure), plane RS gets sheared with respect to PQ (point R1 shears to R2, and S1 shears to S2).
Assuming that the perpendicular distance between PQ and RS is 𝛿 = 25 μm, what is the value of shear strain rate (in s-1 ) that the material undergoes at the shear zone?
GATE ME 2023
3
A CNC machine has one of its linear positioning axes as shown in the figure, consisting of a motor rotating a lead screw, which in turn moves a nut horizontally on which a table is mounted. The motor moves in discrete rotational steps of 50 steps per revolution. The pitch of the screw is 5 mm and the total horizontal traverse length of the table is 100 mm. What is the total number of controllable locations at which the table can be positioned on this axis?
GATE ME 2023
4
The atomic radius of a hypothetical face-centered cubic (FCC) metal is (√2/10) nm. The atomic weight of the metal is 24.092 g/mol. Taking Avogadro’s number to be 6.023 × 1023 atoms/mol, the density of the metal is ____________ kg/m3 .
(Answer in integer)
GATE ME 2023
5
A straight-teeth horizontal slab milling cutter is shown in the figure. It has 4 teeth and diameter (D) of 200 mm. The rotational speed of the cutter is 100 rpm and the linear feed given to the workpiece is 1000 mm/minute. The width of the workpiece (w) is 100 mm, and the entire width is milled in a single pass of the cutter. The cutting force/tooth is given by F = Ktcw, where specific cutting force K = 10 N/mm2, w is the width of cut, and tc is the uncut chip thickness.
The depth of cut (d) is D/2, and hence the assumption of $\frac{d}{D}<<1$ is invalid. The maximum cutting force required is ______ KN (round off to one decimal place).
GATE ME 2022 Set 2
6
In an orthogonal machining operation, the cutting and thrust forces are equal in magnitude. The uncut chip thickness is 0.5 mm and the shear angle is 15°. The orthogonal rake angle of the tool is 0° and the width of cut is 2 mm. The workpiece material is perfectly plastic and its yield shear strength is 500 MPa. The cutting force is _______ N (round off to the nearest integer).
GATE ME 2022 Set 2
7
Under orthogonal cutting condition, a turning operation is carried out on a metallic workpiece at a cutting speed of 4 m/s. The orthogonal rake angle of the cutting tool is 5º. The uncut chip thickness and width of cut are 0.2 mm and 3 mm, respectively. In this turning operation, the resulting friction angle and shear angle are 45º and 25º, respectively. If the dynamic yield shear strength of the workpiece material under this cutting condition is 1000 MPa, then the cutting force is _______ N (round off to one decimal place).
GATE ME 2022 Set 1
8
A 1 mm thick cylindrical tube, 100 mm in diameter, is orthogonally turned such that the entire wall thickness of the tube is cut in a single pass. The axial feed of the tool is 1 m/minute and the specific cutting energy (u) of the tube material is 6 J/mm3. Neglect contribution of feed force towards power. The power required to carry out this operation is _________ kW (round off to one decimal place).
GATE ME 2022 Set 1
9
Two cutting tools with tool life equations given below are being compared:
$$\eqalign{ & Tool\,\,1:\,\,\,\,\,\,\,V{T^{0.1}} = 150 \cr & Tool\,\,2:\,\,\,\,\,\,\,V{T^{0.3}} = 300 \cr} $$
where $$V$$ is cutting speed in $$m/minute$$ and $$T$$ is tool life in minutes. The breakeven cutting speed beyond which Tool $$2$$ will have a higher tool life is _______________ $$m/minute$$.
$$\eqalign{ & Tool\,\,1:\,\,\,\,\,\,\,V{T^{0.1}} = 150 \cr & Tool\,\,2:\,\,\,\,\,\,\,V{T^{0.3}} = 300 \cr} $$
where $$V$$ is cutting speed in $$m/minute$$ and $$T$$ is tool life in minutes. The breakeven cutting speed beyond which Tool $$2$$ will have a higher tool life is _______________ $$m/minute$$.
GATE ME 2017 Set 1
10
During the turning of a $$20$$ $$mm-$$diameter steel bar at a spindle speed of $$400$$ $$rpm,$$ a tool life of $$20$$ minute is obtained. When the same bar is turned at $$200$$ $$rpm,$$ the tool life becomes $$60$$ $$minute.$$ Assume that Taylor's tool life equation is valid. When the bar is turned at $$300$$ $$rpm,$$ the tool life (in minute) is approximately
GATE ME 2017 Set 2
11
In an orthogonal machining with a tool of $${9^ \circ }$$ orthogonal rake angle, the uncut chip thickness is $$0.2$$ $$mm.$$ The chip thickness fluctuates between $$0.25$$ $$mm$$ and $$0.4$$ $$mm.$$ The ratio of the maximum shear angle to the minimum shear angle during machining is ______________
GATE ME 2017 Set 2
12
For a certain job, the cost of metal cutting is $$Rs.18C/V$$ and the cost of tooling is Rs.$$270C/(TV).$$ Where $$C$$ is a constant, $$V$$ is the cutting speed in $$m/min$$ and $$T$$ is the tool life in minutes. The Taylor's tool life equation is $$V{T^{0.25}} = 150.$$ The cutting speed (in $$m/min$$) for the minimum total cost is ___________
GATE ME 2016 Set 2
13
In a single point turning operation with cemented carbide tool and steel work piece, it is found that the Taylor's exponent is $$0.25.$$ If the cutting speed is reduced by $$50\% $$ then the tool life changes by ____________ times.
GATE ME 2016 Set 3
14
For an orthogonal cutting operation, tool material is $$HSS,$$ rake angle is $${22^ \circ },$$ chip thickness is $$0.8$$ $$mm,$$ speed is $$48$$ $$m/min$$ and feed is $$0.4$$ $$mm/rev$$. The shear plane angle (in degrees) is
GATE ME 2016 Set 3
15
The too life equation for $$HSS$$ tool is $$V{T^{0.14}}\,\,{f^{0.7}}\,\,{d^{0.4}} = $$ Constant. The tool life $$(T)$$ of $$30$$ $$min$$ is obtained using the following cutting conditions $$=45$$ $$m/min,$$ $$f=0.35mm,$$ $$d=2.0$$ $$mm.$$ If speed $$(V),$$ feed $$(f)$$ and depth of cut $$(D)$$ are increased individually by $$25\% ,$$ the tool life (in $$min$$) is
GATE ME 2016 Set 1
16
A single point cutting tool with $${0^0}$$ rake angle is used in an orthogonal machining process. At a cutting speed of $$180$$ $$m/min$$ the thrust force is $$490N.$$ If the coefficient of friction between the tool and the chip is $$0.7.$$ Then the power consumption (in $$kW$$) for the machining operation is ____________
GATE ME 2015 Set 2
17
An orthogonal turning operation is carried out under the following conditions; rake angle $$ = {5^ \circ },$$ spindle rotational speed $$=400$$ $$rpm,$$ axial feed $$=0.4$$ $$m/min$$ and radial depth of $$cut = 5mm$$. The chip thickness, $${t_c},$$ is found to be $$3mm.$$ The shear angle (in degrees) in this turning process is ________________
GATE ME 2015 Set 1
18
Orthogonal turning of a mild steel tube with a tool of rake angle $${10^0}$$ is carried out at a feed of $$0.14$$ $$mm/rev.$$ If the thickness of the chip produced is $$0.28mm,$$ the values of shear angle and shear strain will be respectively.
GATE ME 2015 Set 3
19
A cast iron block of $$200$$ $$mm$$ length is being shaped in a shaping machine with a depth of cut of $$4$$ $$mm,$$ feed of $$0.25$$ $$mm/stroke$$ and the tool principal cutting edge angle of $${30^ \circ }.$$ Number of cutting strokes per minutes is $$60.$$ Using specific energy for cutting as $$1.49J/m{m^3},$$ the average power consumption (in Watt) is ___________
GATE ME 2014 Set 4
20
During pure orthogonal turning operation of a hollow cylindrical pipe, it is found that the thickness of the chip produced is $$0.5mm.$$ The feed given to the zero degree rake angle tool is $$0.2mm/rev.$$ The shear strain produced during the operation is ___________
GATE ME 2014 Set 1
21
Which pair of following statement is correct for orthogonal cutting using a single-point cutting tool?
$$P.$$ reduction in friction angle increases cutting force
$$Q.$$ Reduction in friction angle decreases cutting force
$$R.$$ Reduction in friction angle increases chip thickness
$$S.$$ Reduction in friction angle decreases chip thickness
$$P.$$ reduction in friction angle increases cutting force
$$Q.$$ Reduction in friction angle decreases cutting force
$$R.$$ Reduction in friction angle increases chip thickness
$$S.$$ Reduction in friction angle decreases chip thickness
GATE ME 2014 Set 3
22
In orthogonal turning of a bar of $$100$$ $$mm$$ diameter with a feed of $$0.25$$ $$min/rev,$$ depth of cut of $$4$$ $$mm$$ and cutting velocity of $$90$$ $$m/min,$$ it is observed that the main (tangential) cutting force is prependicular to the friction force acting at the chip-tool interface. The main (tangential) cutting force is $$1500$$ $$N.$$
The normal force acting at the chip-tool interface in $$N$$ is
GATE ME 2013
23
In orthogonal turning of a bar of $$100$$ $$mm$$ diameter with a feed of $$0.25$$ $$min/rev,$$ depth of cut of $$4$$ $$mm$$ and cutting velocity of $$90$$ $$m/min,$$ it is observed that the main (tangential) cutting force is prependicular to the friction force acting at the chip-tool interface. The main (tangential) cutting force is $$1500$$ $$N.$$
The orthogonal rake angle of the cutting tool in degrees is
GATE ME 2013
24
Two cutting tools are being compared for a machining operation. The tool life equations are:
$$\eqalign{ & \,\,\,\,\,\,\,\,\,\,\,\,Carbi{\mathop{\rm de}\nolimits} \,\,tool:\,\,\,\,\,\,\,\,\,\,\,\,V{T^{1.6}} = 3000 \cr & \,\,\,\,\,\,\,\,\,\,\,\,HSS\,\,tool:\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,V{T^{0.6}} = 200 \cr} $$
$$\eqalign{ & \,\,\,\,\,\,\,\,\,\,\,\,Carbi{\mathop{\rm de}\nolimits} \,\,tool:\,\,\,\,\,\,\,\,\,\,\,\,V{T^{1.6}} = 3000 \cr & \,\,\,\,\,\,\,\,\,\,\,\,HSS\,\,tool:\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,V{T^{0.6}} = 200 \cr} $$
Where $$V$$ is the cutting speed in $$m/min$$ and $$T$$ is the tool life in $$min.$$ The carbide tool will provide higher tool life if the cutting speed in $$m/min$$ exceeds
GATE ME 2013
25
A single-point cutting tool with $${12^0}$$ rake angle is used to machine a steel work-piece. The depth of cut, $$i.e$$ uncut thickness is $$0.81$$ $$mm.$$ The chip thickness under orthogonal machining condition is $$1.8$$ $$mm.$$ The shear angle is approximately
GATE ME 2011
26
For tool $$A,$$ Taylor’s tool life exponent $$(n)$$ is $$0.45$$ and constant $$(K)$$ is $$90.$$ Similarly for tool $$B,$$ $$n=0.3$$ and $$K=60.$$ The cutting speed (in $$m/min$$) above which tool $$A$$ will have a higher tool life than tool $$B$$ is
GATE ME 2010
27
In a machining experiment, tool life was found to vary with the cutting speed in the following manner
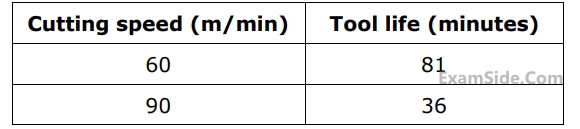
What is percentage increase in tool life when the cutting speed is halved.
GATE ME 2009
28
In a machining experiment, tool life was found to vary with the cutting speed in the following manner
The exponent $$(n)$$ and constant $$(K)$$ of the Taylor's tool life equation are
GATE ME 2009
29
Orthogonal turning is performed on a cylindrical work piece with shear strength of $$250Mpa.$$ The following conditions are used: cutting velocity is $$180m/min,$$ feed is $$0.2mm/rev,$$ depth of cut is $$3mm,$$ chip thickness ratio is $$0.5.$$ The orthogonal rake angle is $$7deg.$$ Apply Merchants theory for analysis,
The cutting and frictional forces respectively are
GATE ME 2008
30
Orthogonal turning is performed on a cylindrical work piece with shear strength of $$250Mpa.$$ The following conditions are used: cutting velocity is $$180m/min,$$ feed is $$0.2mm/rev,$$ depth of cut is $$3mm,$$ chip thickness ratio is $$0.5.$$ The orthogonal rake angle is $$7deg.$$ Apply Merchants theory for analysis,
The shear plane angle (in degrees) and the shear force respectively are
GATE ME 2008
31
In a single point turning tool, the side rake angle and orthogonal rake angle are equal. $$\varphi $$ is the principle cutting edge angle and its range is $$0$$ to $$90.$$ The chip flows in the orthogonal plane. The value of $$\varphi $$ is closer to
GATE ME 2008
32
In orthogonal turning of a low carbon steel bar of diameter $$150mm$$ with uncoated carbide tool, the cutting velocity is $$90m/min,$$ The feed is $$0.24mm/rev$$ and the depth of cut is $$2mm.$$ The chip thickness obtained is $$0.48$$$$mm.$$ If the orthogonal rake angle is zero, and the principle cutting edge angle is $$90,$$ the shear angle in degrees is
GATE ME 2007
33
A low carbon steel bar of $$147$$ $$mm$$ diameter with length of $$630$$ $$mm$$ is being turned with uncoated carbide insert. The observed tool lives are $$24$$ and $$12$$ for cutting velocities of $$90$$ $$m/min$$ and $$120$$ $$m/min$$ respectively. The feed and depth of cut are $$0.2$$ $$mm/rev$$ and $$2$$ $$mm$$ respectively. Use the unmachined diameter to calculate the cutting velocity.
When tool life is $$20min.$$ The cutting velocity in $$m/min$$ is
GATE ME 2007
34
A low carbon steel bar of $$147$$ $$mm$$ diameter with length of $$630$$ $$mm$$ is being turned with uncoated carbide insert. The observed tool lives are $$24$$ and $$12$$ for cutting velocities of $$90$$ $$m/min$$ and $$120$$ $$m/min$$ respectively. The feed and depth of cut are $$0.2$$ $$mm/rev$$ and $$2$$ $$mm$$ respectively. Use the unmachined diameter to calculate the cutting velocity.
Neglect over travel or approach of the tool. When tool life is $$20min,$$ the machining time in $$min$$ for a single pass is
GATE ME 2007
35
In orthogonal turning of low carbon steel pipe with principal cutting edge angle of $$90,$$ the main cutting force is $$1000$$$$N$$ and the feed force is $$800N.$$ The shear angle is $$25$$ and orthogonal rake angle is zero. Employing Merchants theory, the ratio of friction force to the normal force acting on the cutting tool is
GATE ME 2007
36
In orthogonal turning of medium carbon steel, the specific machining energy is $$2$$ $$kJ/m{m^3},$$ the cutting velocity, feed and depth of cut are $$120m/min,$$ $$0.2mm/rev$$ and $$2mm$$ respectively. The main cutting force $$N$$ is
GATE ME 2007
37
In an orthogonal machining operation:
$$\,\,\,\,\,\,\,\,\,\,$$Uncut thickness $$\,\,\,\,\,$$ $$= 0.5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting speed $$\,\,\,\,\,\,\,\,\,\,$$ $$= 20$$ $$m/min$$
$$\,\,\,\,\,\,\,\,\,\,$$Width of cut $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Chip thickness $$\,\,\,\,\,\,\,\,$$ $$= 0.7$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Thrust force$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting force $$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 1200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Rake angle $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = {15^ \circ }$$
Assume Merchant’s theory
$$\,\,\,\,\,\,\,\,\,\,$$Uncut thickness $$\,\,\,\,\,$$ $$= 0.5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting speed $$\,\,\,\,\,\,\,\,\,\,$$ $$= 20$$ $$m/min$$
$$\,\,\,\,\,\,\,\,\,\,$$Width of cut $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Chip thickness $$\,\,\,\,\,\,\,\,$$ $$= 0.7$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Thrust force$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting force $$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 1200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Rake angle $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = {15^ \circ }$$
Assume Merchant’s theory
The values of shear angle and shear strain, respectively are
GATE ME 2006
38
In an orthogonal machining operation:
$$\,\,\,\,\,\,\,\,\,\,$$Uncut thickness $$\,\,\,\,\,$$ $$= 0.5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting speed $$\,\,\,\,\,\,\,\,\,\,$$ $$= 20$$ $$m/min$$
$$\,\,\,\,\,\,\,\,\,\,$$Width of cut $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Chip thickness $$\,\,\,\,\,\,\,\,$$ $$= 0.7$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Thrust force$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting force $$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 1200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Rake angle $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = {15^ \circ }$$
Assume Merchant’s theory
$$\,\,\,\,\,\,\,\,\,\,$$Uncut thickness $$\,\,\,\,\,$$ $$= 0.5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting speed $$\,\,\,\,\,\,\,\,\,\,$$ $$= 20$$ $$m/min$$
$$\,\,\,\,\,\,\,\,\,\,$$Width of cut $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Chip thickness $$\,\,\,\,\,\,\,\,$$ $$= 0.7$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Thrust force$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting force $$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 1200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Rake angle $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = {15^ \circ }$$
Assume Merchant’s theory
The coefficient of friction at the tool chip interface is
GATE ME 2006
39
In an orthogonal machining operation:
$$\,\,\,\,\,\,\,\,\,\,$$Uncut thickness $$\,\,\,\,\,$$ $$= 0.5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting speed $$\,\,\,\,\,\,\,\,\,\,$$ $$= 20$$ $$m/min$$
$$\,\,\,\,\,\,\,\,\,\,$$Width of cut $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Chip thickness $$\,\,\,\,\,\,\,\,$$ $$= 0.7$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Thrust force$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting force $$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 1200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Rake angle $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = {15^ \circ }$$
Assume Merchant’s theory
$$\,\,\,\,\,\,\,\,\,\,$$Uncut thickness $$\,\,\,\,\,$$ $$= 0.5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting speed $$\,\,\,\,\,\,\,\,\,\,$$ $$= 20$$ $$m/min$$
$$\,\,\,\,\,\,\,\,\,\,$$Width of cut $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Chip thickness $$\,\,\,\,\,\,\,\,$$ $$= 0.7$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Thrust force$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting force $$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 1200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Rake angle $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = {15^ \circ }$$
Assume Merchant’s theory
The percentage of total energy dissipated due to friction at the tool chip interface is
GATE ME 2006
40
The figure below shows a graph, which qualitatively relates cutting speed and cost per piece produced.
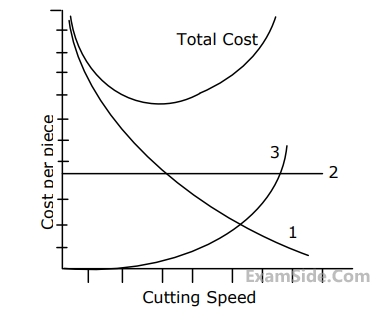
The three curves $$1,2$$ and $$3$$ respectively represent
GATE ME 2005
41
Two tools $$P$$ and $$Q$$ have signature $${5^ \circ } - {5^ \circ } - {6^ \circ } - {6^ \circ } - {8^ \circ } - {30^ \circ } - 0$$ and $${5^ \circ } - {5^ \circ } - {7^ \circ } - {7^ \circ } - {8^ \circ } - {15^ \circ } - 0$$ (both $$ASA$$) respectively. They are used to turn components under the same machining conditions. If $${h_p}$$ and $${h_Q}$$ denote the peak-to-valley height of surfaces produced by the tools $$P$$ and $$Q$$, the ratio $${h_P}/{h_Q}$$ will be
GATE ME 2005
42
In a machining operation, doubling the cutting speed reduces the tool life to $$1/{8^{th}}$$ of the original value. The exponent $$n$$ in Taylor's tool life equation $$V{T^n} = C,$$ is
GATE ME 2004
43
A batch of $$10$$ cutting tools could produce $$500$$ components while working at $$50$$ $$rpm$$ with a tool feed of $$0.25$$ $$mm/rev$$ and depth of cut of $$1$$ $$mm.$$ A similar batch of $$10$$ tools of the same specification could produce $$122$$ components while working at $$80$$ $$rpm$$ with a feed of $$0.25$$ $$mm/rev$$ and $$1$$ $$mm$$ depth of cut. How many components can be produced with one cutting tool at $$60$$ $$rpm$$?
GATE ME 2003
44
During orthogonal cutting of mild steel with a $$10$$ degrees rake angle tool the chip thickness ratio was obtained as $$0.4.$$ The shear angle (in degrees) evaluated from this data is
GATE ME 2001
45
For turning $$NiCr$$ alloy steel at cutting speeds of $$64m/min$$ and $$100m/min,$$ the respective tool lives are $$15min$$ and $$12$$ $$min.$$ The tool life for a cutting speed of $$144m/min$$ is
GATE ME 2001
46
A conventional lathe and a $$CNC$$ lathe are under consideration for machining a given part. The relevant data are shown below :
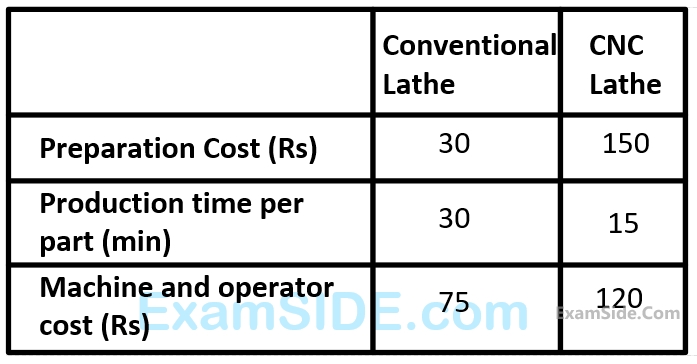
The machine preferred for producing $$100$$ pieces is
GATE ME 2000
47
What is the approximate $$\% $$ change in the life, $$t,$$ of the tool with zero rake angle used in orthogonal cutting when its clearance angle, $$\alpha ,$$ is changed from $$10$$ to $$7$$ deg?
(Hint: flank wear rate is proportional to $$\cot \,\alpha $$)
GATE ME 1999
48
In orthogonal machining operation, the chip thickness and the uncut chip thickness are equal to $$0.45mm$$. If the tool rake angle is $$0$$ deg. The shear plane angle is
GATE ME 1998
49
A cutting tool has a nose radius of $$1.8mm$$. The feed rate for a theoretical surface roughness of $${R_t} = 5$$ microns is
GATE ME 1997
50
In a typical metal cutting operation, using a cutting tool of positive rake $$\gamma = 10\deg ,$$ it was observed that the shear angle was $$20deg$$. The friction angle is
GATE ME 1997
51
In turning operation the feed rate could be doubled to increase the metal removal rate To keep the same level of surface finish, the nose radius of the tool has to be
GATE ME 1989
52
Pure metal pose machinability problem in turning operations. The reason is the
GATE ME 1988
Marks 5
1
In an orthogonal cutting test on mild steel, the following data were obtained
Cutting speed: $$40$$ $$m/min,$$
Depth of cut: $$0.3$$ $$mm,$$
Tool rake angle : $$ + {5^ \circ },$$
Chip thickness: $$1.5$$ $$mm,$$
Cutting force: $$900$$ $$N,$$
Thrust force: $$450$$ $$N$$
Using Merchant's analysis, the Friction angle during the machining will be
Cutting speed: $$40$$ $$m/min,$$
Depth of cut: $$0.3$$ $$mm,$$
Tool rake angle : $$ + {5^ \circ },$$
Chip thickness: $$1.5$$ $$mm,$$
Cutting force: $$900$$ $$N,$$
Thrust force: $$450$$ $$N$$
Using Merchant's analysis, the Friction angle during the machining will be
GATE ME 2004
2
A standard machine tool and an automatic machine tool are being compared for the production of a component. Following data refers to the two machines.
The breakeven production batch size above which the automatic machine tool will be economical to use, will be
GATE ME 2004
3
A cylinder is turned on a lathe with orthogonal machining principle. Spindle rotates at $$200rpm$$. The axial feed rate is $$0.25$$ $$mm$$ per revolution. Depth of cut is $$0.4mm.$$ The rake angle is $${10^ \circ }.$$ In the analysis it is found that the shear angle is $${27.75^ \circ },$$
The thickness of the produced chip is
GATE ME 2003
4
A cylinder is turned on a lathe with orthogonal machining principle. Spindle rotates at $$200rpm$$. The axial feed rate is $$0.25$$ $$mm$$ per revolution. Depth of cut is $$0.4mm.$$ The rake angle is $${10^ \circ }.$$ In the analysis it is found that the shear angle is $${27.75^ \circ },$$
In the above problem, the coefficient of friction at the chip tool interface obtained using Earnest and Merchant theory is
GATE ME 2003
5
A tube of $$32mm$$ outside diameter was turned on a lathe and the following data was obtained
Rake angle $$=35deg,$$
Feed rate $$=0.1mm/rev$$
Cutting force $$=2000N,$$
Cutting speed $$=15m/min$$
Length of continuous chip is one revolution $$=60mm$$
Rake angle $$=35deg,$$
Feed rate $$=0.1mm/rev$$
Cutting force $$=2000N,$$
Cutting speed $$=15m/min$$
Length of continuous chip is one revolution $$=60mm$$
Feed force $$=800N.$$ Calculate the chip thickness, shear plane angle, velocity of chip along tool face and coefficient of friction.
GATE ME 2002
6
Identical straight turning operation was carried out using two tools : $$8 - 8 - 5 - 5 - 5 - 25 - 0\,(ASA)$$ and $$8-8-5-5-7-30-0(ASA)$$. For same feed the tool which gives better surface finish is
GATE ME 2001
7
Tool life testing on a lathe under dry cutting conditions gave $$'n'$$ and $$'C'$$ of Taylor tool life equation as $$0.12$$ and $$130$$ $$m/min,$$ respectively. When a coolant was used, $$'C'$$ increased by $$10\% $$. The increased tool life with the use of coolant at a cutting speed of $$90$$ $$m/min$$ is
GATE ME 2001
8
The lives of two tools $$A$$ & $$B$$, governed by the equation $$V{T^{0.125}} = 2.5$$ and $$V{T^{0.25}} = 7$$ respectively in certain machining operation where $$V$$ is the cutting velocity in $$m/s$$ and $$T$$ is the tool life in sec. Find out the speed $$V$$ at which both the tools will have the same life.
Also calculate the corresponding tool life. If you have to machine at a cutting speed of $$1m/s$$, then which one of these tools will you choose in order to have less frequent tool changes?
GATE ME 1999
9
In an orthogonal cutting experiment with a tool of rake angle $$7$$$$deg$$, the chip thickness was found to be $$2.5mm$$ when the uncut chip thickness was set to $$1mm,$$ find the shear angle $$\phi $$ and find the friction angle $$\beta $$ assuming that Merchants's formula holds good.
GATE ME 1999
10
In a turning trail using orthogonal tool geometry, a chip length of $$84mm$$ was obtained for an uncut chip length of $$200mm.$$ The cutting conditions were $$V=30m/min,$$ $${t_1} = 0.5mm,$$ rake angle $$=20deg,$$ cutting tool is $$HSS.$$ Estimate shear plane angle, chip thickness and the shear plane angle for minimum chip strain.
GATE ME 1997
11
A Throwaway carbide insert was used to machine a steel work pieces with a cutting speed of $$60$$ $$m/min,$$ tool life of $$40$$ minutes was observed, when the cutting speed was increased to $$100$$ $$m/min,$$ the tool life decreased to $$10$$ minutes. The cutting speed for maximum productivity, if tool change time is $$2$$ minutes is
GATE ME 1997
12
Tool life of a $$10$$ hours is obtained when cutting with a single point tool at $$63m/min.$$ If Taylor's constant $$C=257.35,$$ tool life on doubling the velocity will be
GATE ME 1996
13
While turning a $$C15$$ steel of $$160mm$$ diameter at $$215rpm,$$ $$2.5mm$$ depth of cut and feed of $$0.16mm/rev$$ by a tool of geometry $$0-10-8-9-15-75-0mm,$$ the following observations were made. Tangential component of the cutting force $$=500N,$$ axial component of the cutting force $$=200N,$$ chip thickness $$=0.48mm.$$ Determine the dynamic shear strength of the work piece material.
GATE ME 1995
14
If under a condition of plain turning the life of the cutting tool decreases by $$50\% $$ due to increase in the cutting velocity by $$20\% $$, then what is the $$\% $$ increase in tool life due to reduction in the cutting velocity by $$20%$$ from its original value.
GATE ME 1995
15
A single point turning tool is designated as
$$${10^ \circ } - {12^ \circ } - {7^ \circ } - {5^ \circ } - {20^ \circ } - {50^ \circ } - {0^ \circ }\left( {ORS} \right)$$$
The values of normal rake and normal clearance of the above mentioned tool .............
The values of normal rake and normal clearance of the above mentioned tool .............
GATE ME 1995
16
A single point cutting tool made of $$HSS$$ has the value of constant $$'C'$$ $$80,$$ and $$n=0.2$$ in the basic tool life equation. If the tool cost per regrind is Rs $$2$$ and the vmachine hour rate is Rs. $$30,$$ determine the most economical cutting speed (tool cost includes the cost of time spent on changing.
GATE ME 1994
17
A mild steel block of width $$40$$ $$mm$$ is being milled using a straight slab cutter $$70mm$$ diameter with $$30$$teeth. If the cutter rotates at $$40$$$$rpm$$ and the depth of cut is $$2mm,$$ determine the value of maximum uncut chip thickness when the table feed is $$20mm/min$$
GATE ME 1994
18
In an orthogonal cutting operation on a work piece of width $$2.5mm,$$ the uncut chip thickness was $$0.25$$ $$mm$$ and the tool rake angle was $$0$$(zero) degrees. It was observed that the chip thickness was $$1.25mm.$$ The cutting force was measured to be $$900N$$ and the thrust force was found to be $$450N.$$ Find the mean shear strength of the work piece material and if the coefficient of friction between the chip and the tool was $$0.5,$$ what is the machining constant.
GATE ME 1992
19
Determine the Merchants constant $$'C'$$ (shear angle relation) for aluminium from the following orthogonal machining data. Rake angle $${35^ \circ }$$ and an uncut chip thickness $$0.15mm,$$ the values of $${F_c}$$ and $${F_t}$$ are found to be $$200$$ and $$90$$ $$N$$ respectively. The average chip thickness is also measured and found to be $$0.3$$ $$mm,$$ width of cut $$2.5mm$$ and cutting velocity $$30m/min.$$
GATE ME 1991
20
Calculate the $$MRR$$ and Specific cutting pressure for the following cutting conditions
Work material : steel,
Tool material : $$HSS,$$
Depth of cut : $$1.6mm,$$
Feed : $$0.8mm/rev$$
Cutting speed $$=5.5m/min$$ and power consumed $$=0.67$$ $$kW$$
Work material : steel,
Tool material : $$HSS,$$
Depth of cut : $$1.6mm,$$
Feed : $$0.8mm/rev$$
Cutting speed $$=5.5m/min$$ and power consumed $$=0.67$$ $$kW$$
GATE ME 1991
21
Find the percentage change in cutting speed required to give a $$50\% $$ reduction in tool life (that is required tool life is half of the original tool life ) when the value of the tool life exponent $$n=0.125$$ or $$1/8$$.
GATE ME 1991
22
A tube is orthogonally machined in lathe to reduce its length under the following conditions.
Outside diameter of the tube : $$100mm,$$
Inside diameter of the tube $$=96$$ $$mm$$
$$RPM$$ of the work piece $$=120,$$
Longitudinal feed $$=0.5mm/rev$$
Cutting ratio $$=0.3,$$
Tangential force $$=800N,$$
Axial force $$=600N$$
Calculate the chip velocity in $$m/min$$ and the total power consumption in $$KW$$
Outside diameter of the tube : $$100mm,$$
Inside diameter of the tube $$=96$$ $$mm$$
$$RPM$$ of the work piece $$=120,$$
Longitudinal feed $$=0.5mm/rev$$
Cutting ratio $$=0.3,$$
Tangential force $$=800N,$$
Axial force $$=600N$$
Calculate the chip velocity in $$m/min$$ and the total power consumption in $$KW$$
GATE ME 1990
23
The following data is available for machining a component on a turret or center lathe: find out the total number of components to be machined to justify the use of turret lathe
GATE ME 1989
24
In an orthogonal cutting test on the following data were obtained
Uncut chip thickness $$=0.25mm,$$ Cutting speed: $$60m/min,$$ Tool rake angle: $$0$$ Chip thickness $$0.75mm,$$ Cutting force : $$900$$ $$N$$, Thrust force : $$450$$ $$N$$
Uncut chip thickness $$=0.25mm,$$ Cutting speed: $$60m/min,$$ Tool rake angle: $$0$$ Chip thickness $$0.75mm,$$ Cutting force : $$900$$ $$N$$, Thrust force : $$450$$ $$N$$
Calculate the shear angle, total power in making the cut and coefficient of friction between the chip tool interface.
GATE ME 1989
25
The cutting tool are being tried for an operation. Tailors tool life equation for them are as follows
$$\eqalign{ & HSS\,\,tool\,:\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,V{T^{0.1}} = 200 \cr & Carbide\,\,tool\,:\,\,\,\,\,\,\,V{T^{0.35}} = 500 \cr} $$
Find out the break even speed above which the carbide tool will be economical.
$$\eqalign{ & HSS\,\,tool\,:\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,V{T^{0.1}} = 200 \cr & Carbide\,\,tool\,:\,\,\,\,\,\,\,V{T^{0.35}} = 500 \cr} $$
Find out the break even speed above which the carbide tool will be economical.
GATE ME 1989
26
During orthogonal turning of a steel rod by zero rake tool at feed $$0.25mm/rev$$ and depth of cut $$2.0mm,$$ the following observations were obtained. Tangential component of cutting force $$=1000N$$, Axial component of cutting force $$=500N,$$ chip thickness $$=1.0mm,$$ with the help of diagram determine the yield shear strength of work material under the given cutting conditions.
GATE ME 1987
27
In a turning operation the tool life of the carbide tool was found to be $$20min$$ and $$100min,$$ at cutting speeds of $$120m/min$$ and $$80m/min$$ respectively. What will be the tool life of the tool under same condition but at a cutting speed of $$100m/min.$$
GATE ME 1987