Calculus · Engineering Mathematics · GATE ME
Marks 1
1
Let $f(.)$ be a twice differentiable function from $ \mathbb{R}^{2} \rightarrow \mathbb{R}$. If $P, \mathbf{x}_{0} \in \mathbb{R}^{2}$ where $\vert \vert P\vert \vert$ is sufficiently small (here $\vert \vert . \vert \vert$ is the Euclidean norm or distance function), then $f (\mathbf{x}_{0} + p) = f(\mathbf{x}_{0}) + \nabla f(\mathbf{x}_{0})^{T}p + \dfrac{1}{2} p^{T} \nabla^{2}f(\psi)p$ where $\psi \in \mathbb{R}^{2}$ is a point on the line segment joining $\mathbf{x}_{0}$ and $\mathbf{x}_{0} + p$. If $\mathbf{x}_{0}$ is a strict local minimum of $f (\mathbf{x})$, then which one of the following statements is TRUE?
GATE ME 2024
2
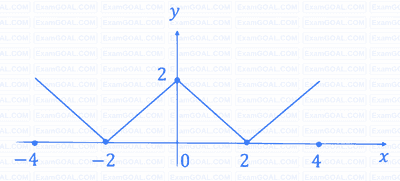
The figure shows the plot of a function over the interval [-4, 4]. Which one of the options given CORRECTLY identifies the function?
GATE ME 2023
3
Given $\int^{\infty}_{-\infty}e^{-x^2}dx=\sqrt{\pi}$
If a and b are positive integers, the value of $\int^{\infty}_{-\infty}e^{-a(x+b)^2}dx$ is _________.
GATE ME 2022 Set 2
4
A polynomial ψ(s) = ansn + an-1sn-1 + ......+ a1s + a0 of degree n > 3 with constant real coefficients an, an-1, ... a0 has triple roots at s = -σ. Which one of the following conditions must be satisfied?
GATE ME 2022 Set 2
5
The limit
$\rm p = \displaystyle\lim_{x \rightarrow \pi} \left( \frac{x^2 + α x + 2 \pi^2}{x - \pi + 2 \sin x} \right)$
has a finite value for a real α. The value of α and the corresponding limit p are
GATE ME 2022 Set 1
6
Define [x] as the greatest integer less than or equal to x, for each x ϵ (-∞, ∞). If y = [x], then area under y for x ϵ [1,4] is
GATE ME 2020 Set 1
7
The value of $$\mathop {\lim }\limits_{x \to 0} \left( {{{{x^3} - \sin \left( x \right)} \over x}} \right)$$ is
GATE ME 2017 Set 1
8
The values of $$x$$ for which the function $$f\left( x \right) = {{{x^2} - 3x - 4} \over {{x^2} + 3x - 4}}$$ is NOT continuous are
GATE ME 2016 Set 2
9
$$\mathop {Lt}\limits_{x \to 0} {{{{\log }_e}\left( {1 + 4x} \right)} \over {{e^{3x}} - 1}}$$ is equal to
GATE ME 2016 Set 3
10
The value of $$\mathop {Lim}\limits_{x \to 0} \left( {{{ - \sin x} \over {2\sin x + x\cos x}}} \right)\,\,\,$$ is __________.
GATE ME 2015 Set 3
11
At $$x=0,$$ the function $$f\left( x \right) = \left| x \right|$$ has
GATE ME 2015 Set 2
12
The value of $$\mathop {Lim}\limits_{x \to 0} \,{{1 - \cos \left( {{x^2}} \right)} \over {2{x^4}}}$$ is
GATE ME 2015 Set 1
13
The value of the integral $$\int\limits_0^2 {{{{{\left( {x - 1} \right)}^2}\sin \left( {x - 1} \right)} \over {{{\left( {x - 1} \right)}^2} + \cos \left( {x - 1} \right)}}dx} $$ is
GATE ME 2014 Set 4
14
$$\mathop {Lt}\limits_{x \to 0} \left( {{{{e^{2x}} - 1} \over {\sin \left( {4x} \right)}}} \right)\,\,$$ is equal to
GATE ME 2014 Set 2
15
If a function is continuous at a point,
GATE ME 2014 Set 3
16
$$\mathop {Lt}\limits_{x \to 0} {{x - \sin x} \over {1 - \cos x}}$$ is
GATE ME 2014 Set 1
17
The value of the definite integral $$\int_1^e {\sqrt x \ln \left( x \right)dx} $$ is
GATE ME 2013
18
Consider the function $$f\left( x \right) = \left| x \right|$$ in the interval $$\,\, - 1 \le x \le 1.\,\,\,$$ At the point $$x=0, f(x)$$ is
GATE ME 2012
19
The area enclosed between the straight line $$y=x$$ and the parabola $$y = {x^2}$$ in the $$x-y$$ plane is
GATE ME 2012
20
$$\,\mathop {Lim}\limits_{x \to 0} \left( {{{1 - \cos x} \over {{x^2}}}} \right)$$ is
GATE ME 2012
21
At $$x=0,$$ the function $$f\left( x \right) = {x^3} + 1$$ has
GATE ME 2012
22
What is $$\mathop {Lim}\limits_{\theta \to 0} {{\sin \theta } \over \theta }\,\,$$ equal to ?
GATE ME 2011
23
A series expansion for the function $$\sin \theta $$ is _______.
GATE ME 2011
24
If $$f(x)$$ is even function and a is a positive real number , then $$\int\limits_{ - a}^a {f\left( x \right)dx\,\,} $$ equals ________.
GATE ME 2011
25
The parabolic are $$y = \sqrt x ,1 \le x \le 2$$ is revolved around the $$x$$-axis. The volume of the solid of revolution is
GATE ME 2010
26
The function $$y = \left| {2 - 3x} \right|$$
GATE ME 2010
27
The value of the integral $$\int\limits_{ - a}^a {{{dx} \over {1 + {x^2}}}} $$
GATE ME 2010
28
The distance between the origin and the point nearest to it on the surface $$\,\,{z^2} = 1 + xy\,\,$$ is
GATE ME 2009
29
The area enclosed between the curves $${y^2} = 4x\,\,$$ and $${{x^2} = 4y}$$ is
GATE ME 2009
30
The value of $$\,\,\mathop {Lim}\limits_{x \to 8} {{{x^{1/3}} - 2} \over {x - 8}}\,\,$$ is
GATE ME 2008
31
In the Taylor series expansion of $${e^x}$$ about $$x=2,$$ the coefficient of $$\,\,{\left( {x - 2} \right)^4}\,\,$$ is
GATE ME 2008
32
The minimum value of function $$\,\,y = {x^2}\,\,$$ in the interval $$\,\,\left[ {1,5} \right]\,\,$$ is
GATE ME 2007
33
$$\int\limits_{ - a}^a {\left[ {{{\sin }^6}\,x + {{\sin }^7}\,x} \right]dx} $$ is equal to
GATE ME 2005
34
Changing the order of integration in the double integral
$${\rm I} = \int\limits_0^8 {\int\limits_{{\raise0.5ex\hbox{$\scriptstyle x$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 4$}}}^2 {f\left( {x,\,y} \right)dy\,dx} } $$ leads to $$\,{\rm I} = \int\limits_r^s {\int\limits_p^q {f\left( {x,\,y} \right)dy\,dx} } .$$ What is $$q$$?
$${\rm I} = \int\limits_0^8 {\int\limits_{{\raise0.5ex\hbox{$\scriptstyle x$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 4$}}}^2 {f\left( {x,\,y} \right)dy\,dx} } $$ leads to $$\,{\rm I} = \int\limits_r^s {\int\limits_p^q {f\left( {x,\,y} \right)dy\,dx} } .$$ What is $$q$$?
GATE ME 2005
35
If $$\,\,\,x = a\left( {\theta + Sin\theta } \right)$$ and $$y = a\left( {1 - Cos\theta } \right)$$ then $$\,\,{{dy} \over {dx}} = \,\_\_\_\_\_.$$
GATE ME 2004
36
Value of the function $$\mathop {Lim}\limits_{x \to a} \,{\left( {x - a} \right)^{x - a}}$$ is _______.
GATE ME 1999
37
Area bounded by the curve $$y = {x^2}$$ and the lines $$x=4$$ and $$y=0$$ is given by
GATE ME 1997
38
If a function is continuous at a point its first derivative
GATE ME 1996
39
The area bounded by the parabola $$2y = {x^2}$$ and the lines $$x=y-4$$ is equal to _________.
GATE ME 1995
40
The value of $$\int\limits_0^\infty {{e^{ - {y^3}}}.{y^{1/2}}} $$ dy is _________.
GATE ME 1994
41
If $$H(x, y)$$ is homogeneous function of degree $$n$$ then $$x{{\partial H} \over {\partial x}} + y{{\partial H} \over {\partial y}} = nH$$
GATE ME 1994
42
$$\mathop {Lim}\limits_{x \to 0} {{x\left( {{e^x} - 1} \right) + 2\left( {\cos x - 1} \right)} \over {x\left( {1 - \cos x} \right)}} = \_\_\_\_\_\_.$$
GATE ME 1993
43
The function $$f\left( {x,y} \right) = {x^2}y - 3xy + 2y + x$$ has
GATE ME 1993
Marks 2
1
If the value of the double integral
$\int_{x=3}^{4} \int_{y=1}^{2} \frac{dydx}{(x + y)^2}$
is $\log_e(\frac{a}{24})$, then $a$ is __________ (answer in integer).
GATE ME 2024
2
A parametric curve defined by $$x = \cos \left( {{{\pi u} \over 2}} \right),y = \sin \left( {{{\pi u} \over 2}} \right)\,\,$$ in the range $$0 \le u \le 1$$ is rotated about the $$x-$$axis by $$360$$ degrees. Area of the surface generated is
GATE ME 2017 Set 1
3
$$\mathop {Lt}\limits_{x \to \infty } \left( {\sqrt {{x^2} + x - 1} - x} \right)$$ is
GATE ME 2016 Set 3
4
Consider the function $$f\left( x \right) = 2{x^3} - 3{x^2}\,\,$$ in the domain $$\,\left[ { - 1,2} \right].$$ The global minimum of $$f(x)$$ is _________.
GATE ME 2016 Set 1
5
Consider a spatial curve in three -dimensional space given in parametric form by $$\,\,x\left( t \right)\,\, = \,\,\cos t,\,\,\,y\left( t \right)\,\, = \,\,\sin t,\,\,\,z\left( t \right)\,\, = \,\,{2 \over \pi }t,\,\,\,0 \le t \le {\pi \over 2}.$$ The length of the curve is ________.
GATE ME 2015 Set 1
6
Consider an ant crawling along the curve $$\,{\left( {x - 2} \right)^2} + {y^2} = 4,$$ where $$x$$ and $$y$$ are in meters. The ant starts at the point $$(4, 0)$$ and moves counter $$-$$clockwise with a speed of $$1.57$$ meters per second. The time taken by the ant to reach the point $$(2, 2)$$ is _________ (in seconds).
GATE ME 2015 Set 1
7
The value of the integral $$\,\int\limits_0^2 {\int\limits_0^x {{e^{x + y}}\,\,dy} } $$ $$dx$$ is
GATE ME 2014 Set 4
8
A political party orders an arch for the entrance to the ground in which the annual convention is being held. The profile of the arch follows the equation $$y = 2x\,\,\, - 0.1{x^2}$$ where $$y$$ is the height of the arch in meters. The maximum possible height of the arch is
GATE ME 2012
9
The infinite series $${\,f\left( x \right) = x - {{{x^3}} \over {3!}} + {{{x^5}} \over {5!}} - {{{x^7}} \over {7!}} + - - - \,\,}$$ Converges to
GATE ME 2010
10
Let $$\,\,f = {y^x}.$$ What is $$\,\,{{{\partial ^2}f} \over {\partial x\partial y}}\,\,$$ at $$x=2,$$ $$y=1$$?
GATE ME 2008
11
The length of the curve $$\,y = {2 \over 3}{x^{3/2}}$$ between $$x=0$$ & $$x=1$$ is
GATE ME 2008
12
Which of the following integrals is unbounded?
GATE ME 2008
13
Consider the shaded triangular region $$P$$ shown in the figure. What is $$\int\!\!\!\int\limits_p {xy\,dx\,dy\,?} $$
GATE ME 2008
14
If $$\,\,\,y = x + \sqrt {x + \sqrt {x + \sqrt {x + .....\alpha } } } \,\,\,$$ then $$y(2)=$$ __________.
GATE ME 2007
15
$$\mathop {Lim}\limits_{x \to 0} {{{e^x} - \left( {1 + x + {{{x^2}} \over 2}} \right)} \over {{x^3}}} = $$
GATE ME 2007
16
By a change of variables $$x(u, v) = uv,$$ $$\,\,y\left( {u,v} \right) = {v \over u}$$ in a double integral, the integral $$f(x, y)$$ changes to $$\,\,\,f\left( {uv,{\raise0.5ex\hbox{$\scriptstyle v$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle u$}}} \right).\,\,\,$$ Then $$\,\,\phi \left( {u,v} \right)\,\,\,$$ is ________.
GATE ME 2005
17
The volume of an object expressed in spherical co-ordinates is given by
$$V = \int\limits_0^{2\pi } {\int\limits_0^{{\raise0.5ex\hbox{$\scriptstyle \pi $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}} {\int\limits_0^1 {{r^2}} \,Sin\phi \,drd\phi \,d\theta .} } $$ The value of the integral
$$V = \int\limits_0^{2\pi } {\int\limits_0^{{\raise0.5ex\hbox{$\scriptstyle \pi $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}} {\int\limits_0^1 {{r^2}} \,Sin\phi \,drd\phi \,d\theta .} } $$ The value of the integral
GATE ME 2004