Radiation · Heat Transfer · GATE ME
Marks 1
During a welding operation, thermal power of 2500 W is incident normally on a metallic surface. As shown in the figure below (figure is NOT to scale), the heated area is circular. Out of the incident power, $85 \%$ of the power is absorbed within a circle of radius 5 mm while $65 \%$ is absorbed within an inner concentric circle of radius 3 mm . The power density in the shaded area is __________ $\mathrm{Wmm}^{-2}$ (rounded off to 2 decimal places).

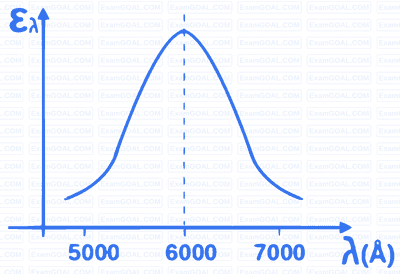
Wien’s law is stated as follows: λmT = C, where C is 2898 μm.K and λm is the wavelength at which the emissive power of a black body is maximum for a given temperature T. The spectral hemispherical emissivity (ελ) of a surface is shown in the figure below (1 Å = 10-10 m). The temperature at which the total hemispherical emissivity will be highest is K (round off to the nearest integer).
A flat plate made of cast iron is exposed to a solar flux of 600 W/m2 at an ambient temperature of 25 °C. Assume that the entire solar flux is absorbed by the plate. Cast iron has a low-temperature absorptivity of 0.21. Use Stefan-Boltzmann constant = 5.669 × 10-8 W/m2-K4. Neglect all other modes of heat transfer except radiation. Under the aforementioned conditions, the radiation equilibrium temperature of the plate is __________ °C (round off to the nearest integer).
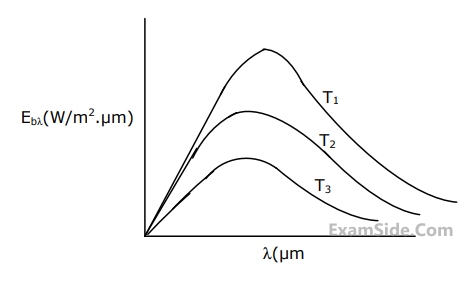
The conclusion is that the measurements are
The temperature and emissivity values for the surfaces of the room are $$300$$ $$K$$ and $$0.3$$ respectively. Boltzmannn constant $$\sigma = 5.67 \times {10^{ - 8}}\,\,W/{m^2}{K^4}.$$ The total heat loss from the two surfaces of the plate is
Marks 2
Consider a cylindrical furnace of 5 m diameter and 5 m length with bottom, top and curved surfaces maintained at uniform temperatures of $800 \mathrm{~K}, 1500 \mathrm{~K}$ and 500 K , respectively. The view factor between the bottom and top surfaces, $F_{12}$ is 0.2 . The magnitude of net radiation heat transfer rate between the bottom surface and the curved surface is _________ kW (rounded off to 1 decimal place).
All surfaces of the furnace can be assumed as black.
The Stefan-Boltzmann constant, $\sigma=5.67 \times 10^{-8} \mathrm{~W} \mathrm{~m}^{-2} \mathrm{~K}^{-4}$.

Consider a hemispherical furnace of diameter $ D = 6 \text{ m} $ with a flat base. The dome of the furnace has an emissivity of 0.7 and the flat base is a blackbody. The base and the dome are maintained at uniform temperature of 300 K and 1200 K, respectively. Under steady state conditions, the rate of radiation heat transfer from the dome to the base is _______ kW (rounded off to the nearest integer).
Use Stefan-Boltzmann constant = $5.67 \times 10^{-8} \text{ W/(m}^2 \text{ K}^4 \text{)}$

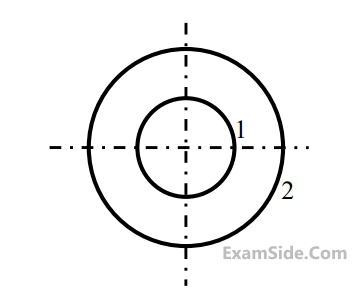
The view-factor FS-S is
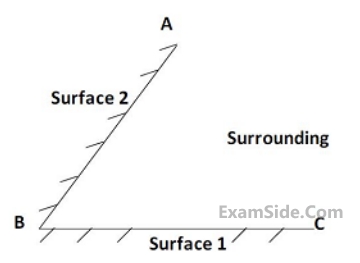
while the side walls are at temperature $${T_2} = {T_4} = {527^ \circ }C.$$
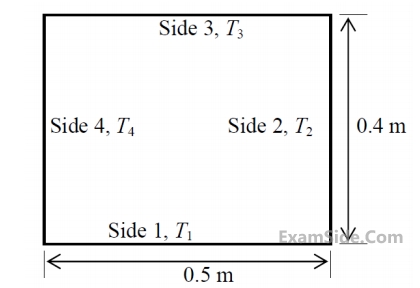
The view factor, $${F_{1 - 2}}$$ is $$0.26.$$ The net radiation heat loss or gain on side $$1$$ is_________ $$W/m.$$ Stefan-Boltzman constant $$ = \,5.67 \times {10^{ - 8}}$$ $$W/{m^2}$$-$${K^4}$$
Given emissivity values, $${\varepsilon _1} = 0.5,\,\,{\varepsilon _2} = 0.25$$ and Stefan-Boltzmann constant $$\sigma = 5.67 \times {10^{ - 8}}\,$$ $$\,W/{m^2}$$-$$K,$$ the heat transfer between the plates (in $$kW/{m^2}$$) is _____________.
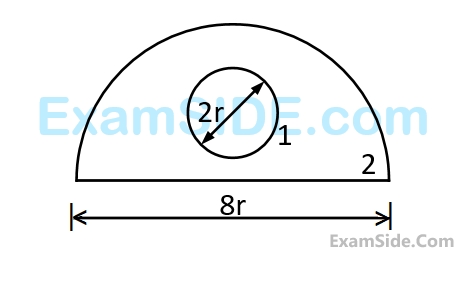
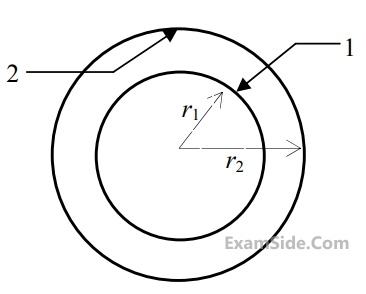
The view factor $${F_{21}}$$ for radiation heat transfer is
$$5.67 \times {10^{ - 8}}\,W/{m^2}{K^4}$$
The irradiation (in $$kW/{m^2}$$) for the upper plate is
$$5.67 \times {10^{ - 8}}\,W/{m^2}{K^4}$$
If plate is also a diffuse gray surface with an emisivity value of $$0.8,$$ the net radiant heat exchange (in $$kW/{m^2}$$) between plate $$1$$ and plate $$2$$
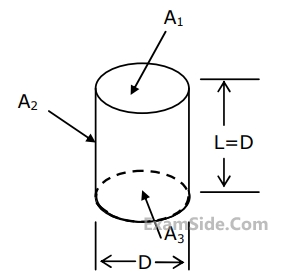
Marks 5
Use $$\sigma = 5.67 \times {10^{ - 8}}W/\left( {{m^2}{K^4}} \right)$$
Stephen Boltzmann constant $$5.67 \times {10^{ - 8}}\,\,W/{m^2}{K^4}$$. View factor between two parallel square plates placed directly opposite to each other is $$0.2$$