Pert and Cpm · Industrial Engineering · GATE ME

The standard deviation of linear dimensions $$P$$ and $$Q$$ are $$3\mu m$$ and $$4\mu m$$, respectively. When assembled, the standard deviation (in $$\mu m$$) of the following linear dimension $$(P+Q)$$ is ___________.

In $$PERT$$ chart, the activity time distribution is

A minimal spanning tree in network flow models involves

The expected time $$\left( {{t_e}} \right)$$ of a $$PERT$$ activity in terms of optimistic time $$\left( {{t_0}} \right)$$, pessimistic $$\left( {{t_p}} \right)$$ and most likely time $$\left( {{t_L}} \right)$$ is given by

In $$PERT$$ analysis a critical activity has

A dummy activity is used in $$PERT$$ network to describe

In $$PERT,$$ the distribution of activity times is assumed to be

A project consists of five activities (A, B, C, D and E). The duration of each activity follows beta distribution. The three time estimates (in weeks) of each activity and immediate predecessor(s) are listed in the table. The expected time of the project completion is ______ weeks (in integer).

Activity	Time estimates (in weeks)			Immediate predecessor(s)
	Optimistic time	Most likely time	Pessimistic time
A	4	5	6	None
B	1	3	5	A
C	1	2	3	A
D	2	4	6	C
E	3	4	5	B, D

Activities A to K are required to complete a project. The time estimates and the immediate predecessors of these activities are given in the table. If the project is to be completed in the minimum possible time, the latest finish time for the activity G is ______ hours.

$$ \begin{array}{|c|c|c|} \hline \text { Activity } & \text { Time (hours) } & \text { Immediate predecessors } \\ \hline \text { A } & 2 & - \\ \hline \text { B } & 3 & - \\ \hline \text { C } & 2 & - \\ \hline \text { D } & 4 & \text { A } \\ \hline \text { E } & 5 & \text { B } \\ \hline \text { F } & 4 & \text { B } \\ \hline \text { G } & 3 & \text { C } \\ \hline \text { H } & 10 & \text { D, E } \\ \hline \text { I } & 5 & \text { F } \\ \hline \text { J } & 8 & \text { G } \\ \hline \text { K } & 3 & \text { H, I, J } \\ \hline \end{array} $$

A project starts with activity $$A$$ and ends with activity $$F.$$ The precedence relation and durations of the activities are as per the following table:

The minimum project completion time (in days) is ___________

A project consists of $$14$$ activities, $$A$$ to $$N$$. The duration of these activities (in days) are shown in brackets on the network diagram. The latest finish time (in days) for node $$10$$ is _____________

A project consists of $$7$$ activities. The network along with the time durations (in days) for various activities is shown in the figure.

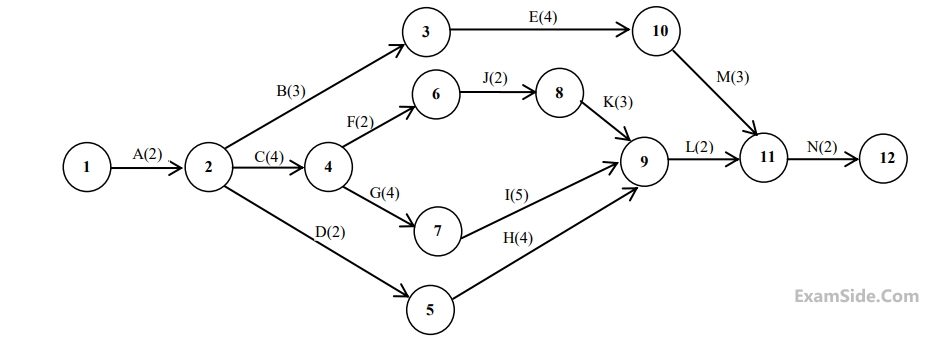
The minimum time (in days) for completion of the project is _____________

Following data refers to the activities of a project, where, node $$1$$ refers to the start and node $$5$$ refers to the end of the project.

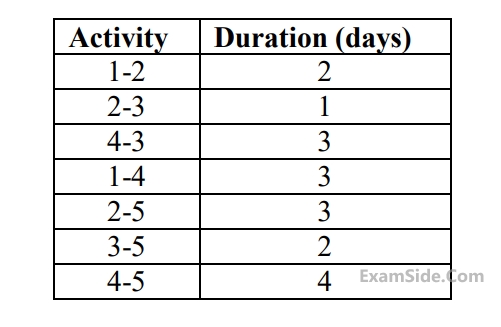
The critical path $$(CP)$$ in the network is

The precedence relations and duration (in days) of activities of a project network are given in the table. The total float (in days) of activities $$e$$ and $$f,$$ respectively, are

A project has four activities $$P,Q, R$$ and $$S$$ as shown below.

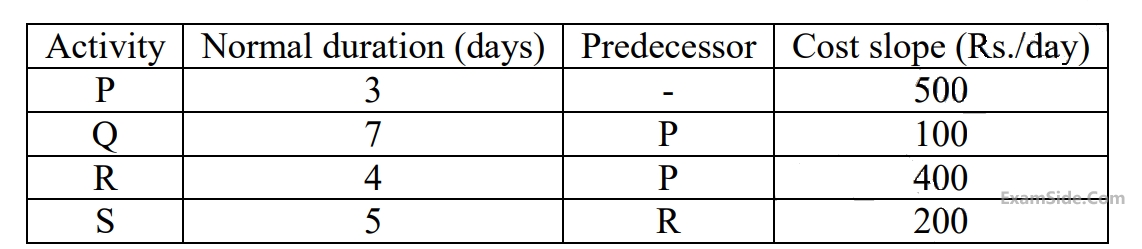
The normal cost of the project is Rs. $$10,000/-$$ and the overhead cost is Rs. $$200/-$$ per day. If the project duration has to be crashed down to $$9$$ days, the total cost (in Rupees) of the project is ______________.

Consider the given project network, where numbers along various activities represent the normal time. The free float on activity $$4$$-$$6$$ and the project duration, respectively, are

For a particular project, eight activities are to be carried out. Their relationships with other activities and expected durations are mentioned in the table below.

The critical path for the project is

For a particular project, eight activities are to be carried out. Their relationships with other activities and expected durations are mentioned in the table below.

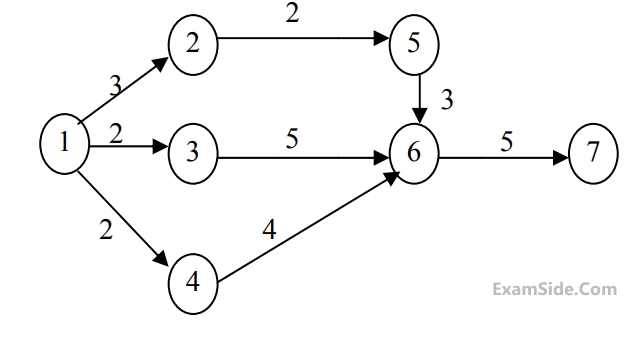
If the duration of activity $$''f ''$$ alone is changed from $$9$$ to $$10$$ days, then the

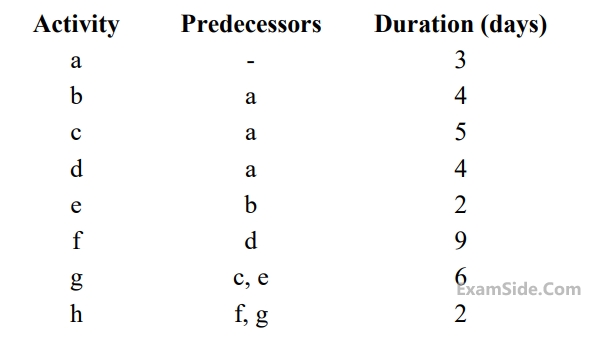
The project activities, precedence relationships and durations are described in the table. The critical path of the project is

Consider the following network

The optimistic time, most likely time and pessimistic time of all the activities are given in the table below :

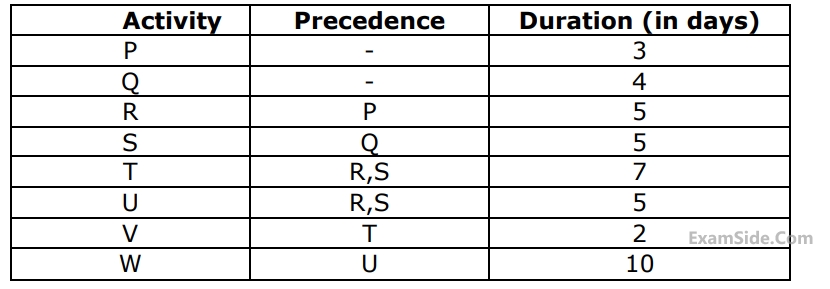
The critical path duration of the network (in days) is

Consider the following network

The optimistic time, most likely time and pessimistic time of all the activities are given in the table below :

The standard deviation of the critical path is

For the network below, the objective is to find the length of the shortest path from node $$P$$ to node $$G.$$ Let $${d_{ij}}$$ be the length of directed are from node $$i$$ to node $$j$$. Let $${s_j}$$ be the length of the shortest path from $$P$$ to node $$j.$$ Which of the following equations can be used to find $${s_G}$$?

Consider a $$PERT$$ network for a project involving six tasks ($$a$$ to $$f$$)

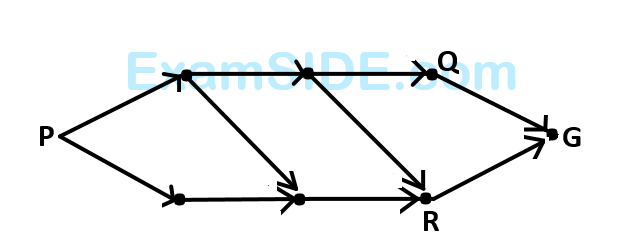
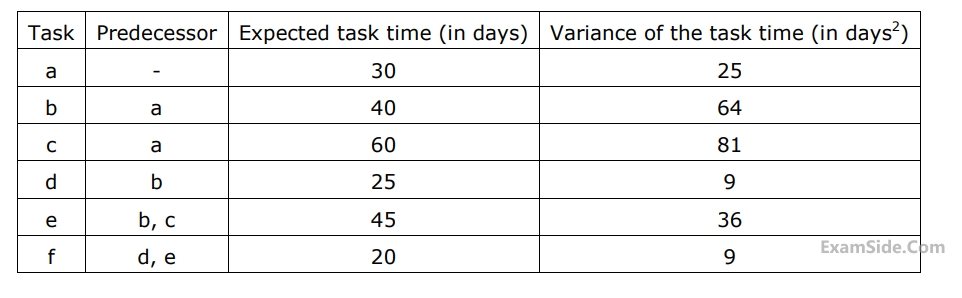
The expected completion time of the project is

Consider a $$PERT$$ network for a project involving six tasks ($$a$$ to $$f$$)

The standard deviation of the critical path of the project is

A project has six activities $$(A$$ to $$F)$$ with respective activity durations $$7,5,6,6,8,4$$ days. The network has three paths $$A-B,C-D$$ and $$E-F.$$ All the activities can be crashed with the same crash cost per day. The number of activities that need to be crashed to reduce the project duration by $$1$$ day is

A project consists of activities $$A$$ to $$M$$ shown in the net in the following figure with the duration of the activities marked in days.

The project can be completed

A project consists of three parallel paths with mean durations and variances of $$(10,4), (12,4)$$ and $$(12,9)$$ respectively. According to the standard $$PERT$$ assumptions, the distribution of the project duration is

In the construction of networks, dummy activities are introduced in order to :

The precedence relations and durations of jobs in a project are given below:
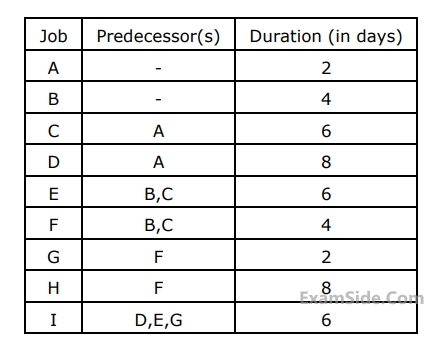
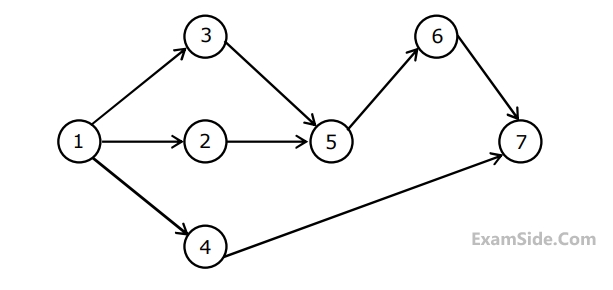
(a) Draw the activity-on-arc project network
(b) Determine all critical path(s) and their duration(s).
(c) What is the total float for jobs $$B$$ and $$D?$$

Given below are the data for a project network.
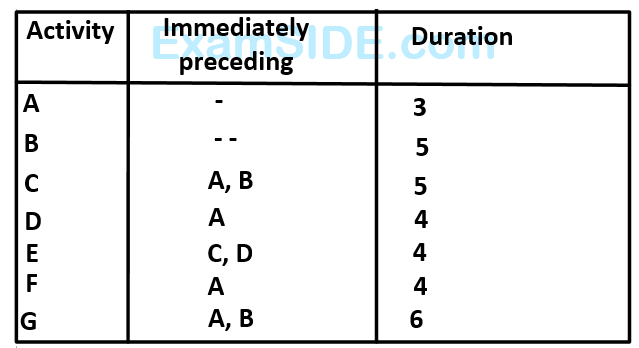
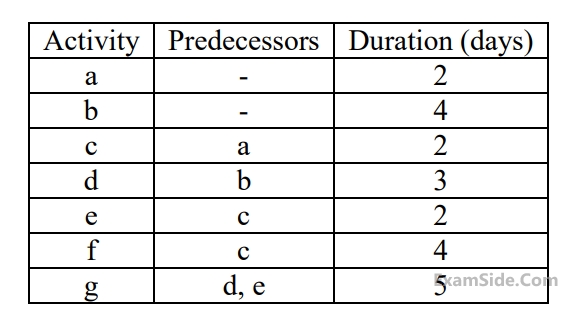
(a) Draw the network for the above project capturing the precedence relationships.
(b) Find the critical path and its duration.

A project plan is given below:

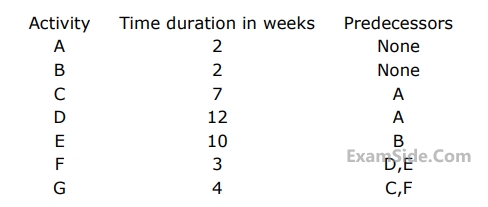
(a) Construct a $$PERT$$ network
(b) Find the critical path and estimate the project duration.

A project with the following data is to be implemented:

(a) What is the minimum duration of the project?
(b) Draw a Gantt chart for the early schedule
(c) Determine the peak requirement of money and the day on which it occurs in above schedule.

For a small project with five jobs, the following data is given
(i) Draw the project network in activity on arc mode
(ii) Under $$PERT$$ assumptions, determine the distribution of project duration.