Transform Theory · Engineering Mathematics · GATE ME
Marks 1
1
F(t) is a periodic square wave function as shown. It takes only two values, 4 and 0, and stays at each of these values for 1 second before changing. What is the constant term in the Fourier series expansion of F(t)?
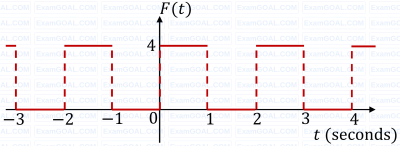
GATE ME 2022 Set 2
2
The Fourier series expansion of x3 in the interval −1 ≤ x < 1 with periodic continuation has
GATE ME 2022 Set 1
3
The Laplace transform of $${e^{i5t}}$$ where $$i = \sqrt { - 1} ,$$
GATE ME 2015 Set 2
4
Laplace transform of $$\cos \left( {\omega t} \right)$$ is
GATE ME 2015 Set 2
5
The Laplace Transform of $$f\left( t \right) = {e^{2t}}\sin \left( {5t} \right)\,u\left( t \right)$$ is
GATE ME 2015 Set 1
6
Laplace transform of the function $$f(t)$$ is given by $$f\left( s \right) = L\left\{ {f\left( t \right)} \right\} = \int\limits_0^\infty {f\left( t \right){e^{ - st}}\,dt.} $$

Laplace transform of the function shown below is given by.

GATE ME 2015 Set 3
7
Laplace transform of $$\cos \,\left( {\omega t} \right)$$ is $${s \over {{s^2} + {\omega ^2}.}}$$. The Laplace transform of $${e^{ - 2t}}\,\cos \left( {4t} \right)$$ is
GATE ME 2014 Set 4
8
The function $$f(t)$$ satisfies the differential equation $${{{d^2}f} \over {d{t^2}}} + f = 0$$ and the auxiliary conditions, $$f\left( 0 \right) = 0,\,{{df} \over {dt}}\left( 0 \right) = 4.$$ The laplace transform of $$f(t)$$ is given by
GATE ME 2013
9
The inverse Laplace transform of the function $$F\left( s \right) = {1 \over {s\left( {s + 1} \right)}}$$ is given by
GATE ME 2012
10
The Laplace transform of $$f\left( t \right)$$ is $${1 \over {{s^2}\left( {s + 1} \right)}}.$$
The function
The function
GATE ME 2010
11
The inverse Laplace transform of $${1 \over {\left( {{s^2} + s} \right)}}$$ is
GATE ME 2009
12
If $$F(s)$$ is the Laplace transform of the function $$f(t)$$ then Laplace transform of $$\int\limits_0^t {f\left( x \right)dx} $$ is
GATE ME 2007
13
Laplace transform of $${\left( {a + bt} \right)^2}$$ where $$'a'$$ and $$'b'$$ are constants is given by:
GATE ME 1999
14
Solve the initial value problem
$${{{d^2}y} \over {d{x^2}}} - 4{{dy} \over {dx}} + 3y = 0$$ with $$y=3$$ and
$${{dy} \over {dx}} = 7$$ at $$x=0$$ using the laplace transform technique?
$${{{d^2}y} \over {d{x^2}}} - 4{{dy} \over {dx}} + 3y = 0$$ with $$y=3$$ and
$${{dy} \over {dx}} = 7$$ at $$x=0$$ using the laplace transform technique?
GATE ME 1997
15
If $$f(t)$$ is a finite and continuous Function for $$t \ge 0$$ the laplace transformation is given by
$$F = \int\limits_0^\infty {{e^{ - st}}\,\,f\left( t \right)dt,} $$ then for $$f(t)=cos$$ $$h$$ $$mt,$$ the laplace transformation is ___________.
$$F = \int\limits_0^\infty {{e^{ - st}}\,\,f\left( t \right)dt,} $$ then for $$f(t)=cos$$ $$h$$ $$mt,$$ the laplace transformation is ___________.
GATE ME 1994
16
The laplace transform of the periodic function $$f(t)$$ described by the curve below
$$i.e.\,\,f\left( t \right) = \left\{ {\matrix{ {\sin \,t,} & {if\left( {2n - 1} \right)\pi < t < 2n\pi \left( {n = 1,2,3,...} \right)} \cr 0 & {otherwise\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \cr } } \right.$$ is ___________.
$$i.e.\,\,f\left( t \right) = \left\{ {\matrix{ {\sin \,t,} & {if\left( {2n - 1} \right)\pi < t < 2n\pi \left( {n = 1,2,3,...} \right)} \cr 0 & {otherwise\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \cr } } \right.$$ is ___________.

GATE ME 1993