A project consists of five activities (A, B, C, D and E). The duration of each activity follows beta distribution. The three time estimates (in weeks) of each activity and immediate predecessor(s) are listed in the table. The expected time of the project completion is ______ weeks (in integer).

Activity	Time estimates (in weeks)			Immediate predecessor(s)
	Optimistic time	Most likely time	Pessimistic time
A	4	5	6	None
B	1	3	5	A
C	1	2	3	A
D	2	4	6	C
E	3	4	5	B, D

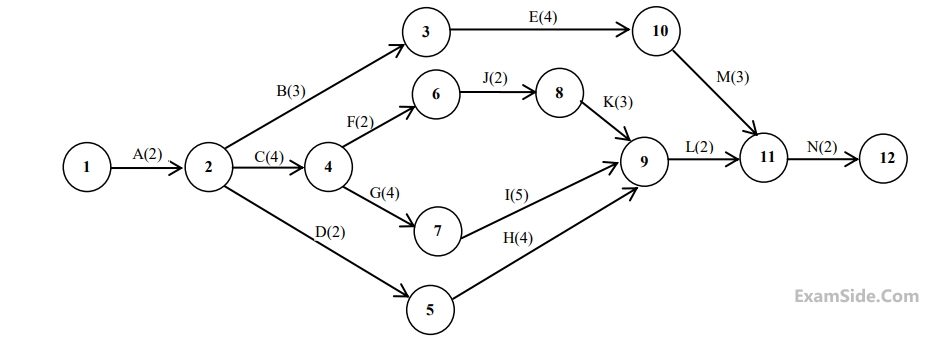
Activities A to K are required to complete a project. The time estimates and the immediate predecessors of these activities are given in the table. If the project is to be completed in the minimum possible time, the latest finish time for the activity G is ______ hours.

$$ \begin{array}{|c|c|c|} \hline \text { Activity } & \text { Time (hours) } & \text { Immediate predecessors } \\ \hline \text { A } & 2 & - \\ \hline \text { B } & 3 & - \\ \hline \text { C } & 2 & - \\ \hline \text { D } & 4 & \text { A } \\ \hline \text { E } & 5 & \text { B } \\ \hline \text { F } & 4 & \text { B } \\ \hline \text { G } & 3 & \text { C } \\ \hline \text { H } & 10 & \text { D, E } \\ \hline \text { I } & 5 & \text { F } \\ \hline \text { J } & 8 & \text { G } \\ \hline \text { K } & 3 & \text { H, I, J } \\ \hline \end{array} $$

A project starts with activity $$A$$ and ends with activity $$F.$$ The precedence relation and durations of the activities are as per the following table:

The minimum project completion time (in days) is ___________

A project consists of $$14$$ activities, $$A$$ to $$N$$. The duration of these activities (in days) are shown in brackets on the network diagram. The latest finish time (in days) for node $$10$$ is _____________