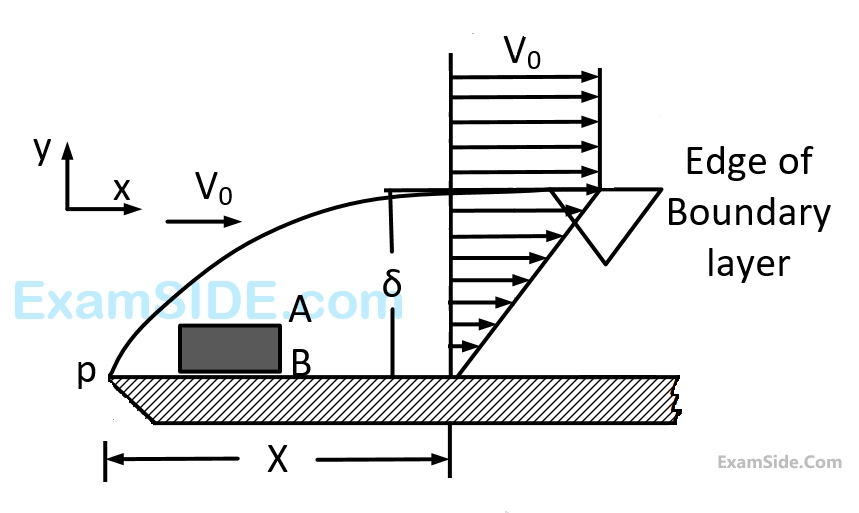
Marks 1
$${{dP} \over {dx}} > 0$$
Marks 2
given by $$u = {U_0}\left[ {2\left( {{y \over \delta }} \right) - {{\left( {{y \over \delta }} \right)}^2}} \right]$$
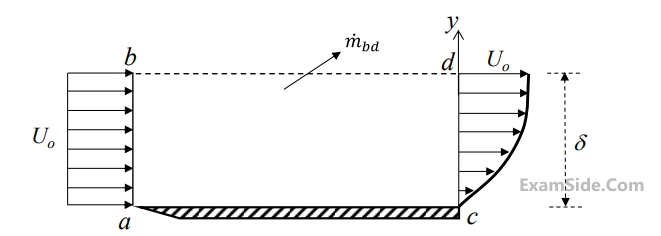
The ratio of the mass flow rate, $$\mathop {m{}_{bd}}\limits^ \bullet ,$$ leaving through the horizontal section $$b$$-$$d$$ to that entering through the vertical section $$a$$-$$b$$ is
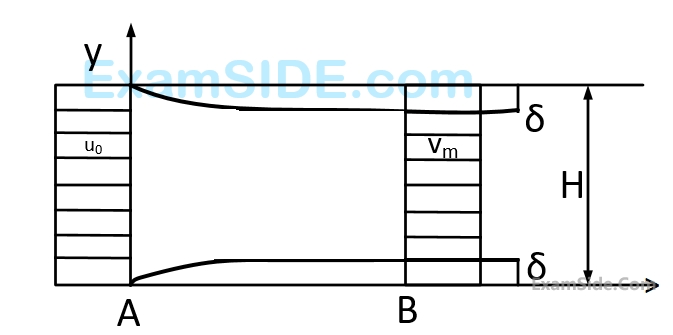
The velocity profile is uniform with a value of $${u_0}$$ at the inlet section $$A$$. The velocity profile at section B down stream is
$$$u\left\{ {\matrix{ {{V_m}{y \over \delta },} & {0 \le y \le \delta } \cr {{V_m},} & {\delta \le y \le H - \delta } \cr {{V_m}{{H - y} \over \delta },} & {H - \delta \le y \le H} \cr } } \right.$$$The ratio $${{{V_m}} \over {{u_0}}}$$ is

The velocity profile is uniform with a value of $${u_0}$$ at the inlet section $$A$$. The velocity profile at section B down stream is
$$$u\left\{ {\matrix{ {{V_m}{y \over \delta },} & {0 \le y \le \delta } \cr {{V_m},} & {\delta \le y \le H - \delta } \cr {{V_m}{{H - y} \over \delta },} & {H - \delta \le y \le H} \cr } } \right.$$$The ratio $${{{P_A} - {P_B}} \over {{1 \over 2}\rho {u_0}^2}}$$ (where $${{P_A}}$$ and $${{P_B}}$$ are the pressure at section $$A$$ and $$B$$ respectively and $$\rho $$ is the density of the fluid ) is
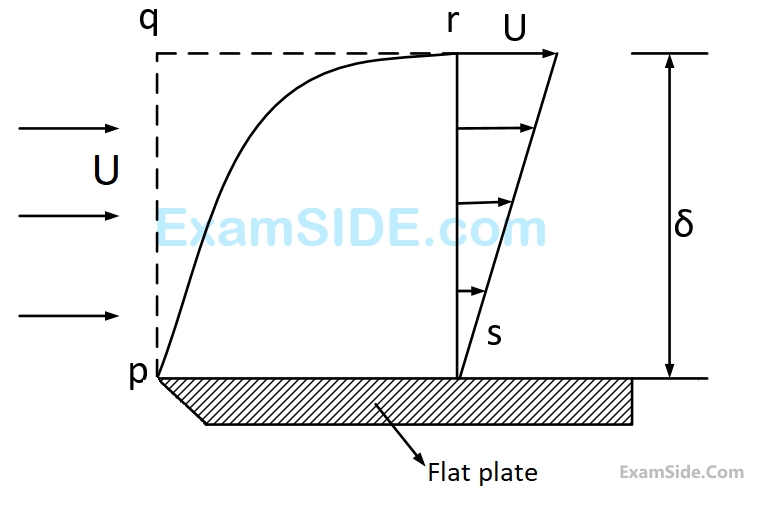
The mass flow rate (in kg/s) across the section $$q$$-$$r$$ is

The integrated drag force (in $$N$$) on the plate, between $$p$$-$$s$$, is
If the free stream velocity is $$2$$ $$m/s$$, and air has Kinematic viscosity of $$1.5 \times {10^{ - 5}}{m^2}/s$$ and density of $$1.23$$ $$kg/{m^3}$$, then wall shear stress at $$x=1$$ $$m$$, is