Vibrations · Theory of Machines · GATE ME
Marks 1
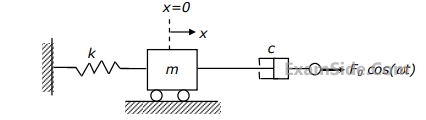
A linear spring-mass-dashpot system with a mass of 2 kg is set in motion with viscous damping. If the natural frequency is 15 Hz, and the amplitudes of two successive cycles measured are 7.75 mm and 7.20 mm, the coefficient of viscous damping (in N.s/m) is
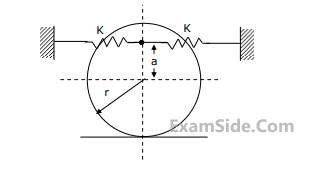
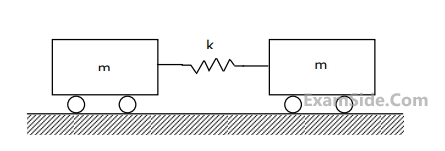
The figure shows a block of mass m = 20 kg attached to a pair of identical linear springs, each having a spring constant k = 1000 N/m. The block oscillates on a frictionless horizontal surface. Assuming free vibrations, the time taken by the block to complete ten oscillations is _________ seconds. (Rounded off to two decimal places)
Take π = 3.14.

For a dynamical system governed by the equation,
$\ddot{x}(t)+2 ζ \omega_n \dot{x}(t)+\omega_n^2x(t)=0$
the damping ratio ζ is equal to $\frac{1}{2\pi}\log_e2$. The displacement x of this system is measured during a hammer test. A displacement peak in the positive displacement direction is measured to be 4 mm. Neglecting higher powers (> 1) of the damping ratio, the displacement at the next peak in the positive direction will be _______ mm (in integer).
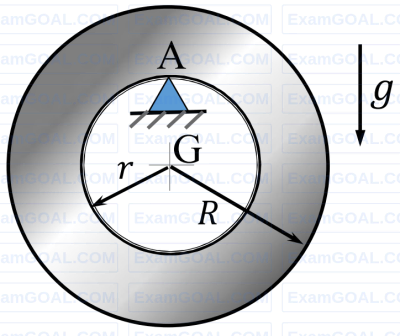
A rigid uniform annular disc is pivoted on a knife edge A in a uniform gravitational field as shown, such that it can execute small amplitude simple harmonic motion in the plane of the figure without slip at the pivot point. The inner radius r and outer radius 𝑅 are such that r2 = R2/2, and the acceleration due to gravity is g. If the time period of small amplitude simple harmonic motion is given by $T = β π \sqrt{R/g} $ where π is the ratio of circumference to diameter of a circle, then β = ________ (round off to 2 decimal places).
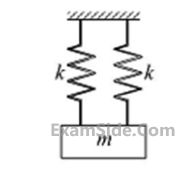
$$P.$$ For a system having critical damping, the value of damping ratio is unity and system does not undergo a vibratory motion.
$$Q.$$ Logarithmic decrement method is used to determine the amount of damping in a physical system.
$$R.$$ In case of damping due to dry friction between moving surfaces resisting force of constant magnitude acts opposite to the relative motion.
$$S.$$ For the case of viscous damping, drag force is directly proportional to the square of relative velocity.
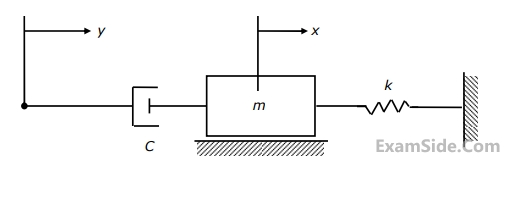
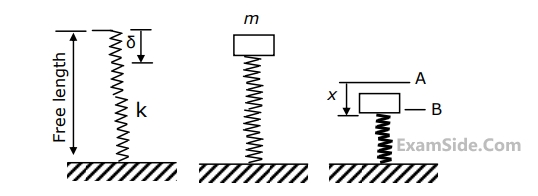
Marks 2
The system shown in the figure below consists of a cantilever beam (with flexural rigidity El and negligible mass), a spring (with spring constant $K$ and negligible mass) and a block of mass $m$. Assuming a lumped parameter model for the system, the fundamental natural frequency $\left(\omega_n\right)$ of the system is

A vibratory system consists of mass $m$, a vertical spring of stiffness $2k$ and a horizontal spring of stiffness $k$. The end $A$ of the horizontal spring is given a horizontal motion $x_A = a \sin \omega t$. The other end of the spring is connected to an inextensible rope that passes over two massless pulleys as shown.
Assume $m = 10 kg$, $k = 1.5$ kN/m, and neglect friction.
The magnitude of critical driving frequency for which the oscillations of mass $m$ tend to become excessively large is _____ rad/s (answer in integer).

A spring mass damper system (mass m, stiffness k, and damping coefficient c) excited by a force F(t) = B sin ωt, where B, ω and t are the amplitude, frequency and time, respectively, is shown in the figure. Four different responses of the system (marked as (i) to (iv)) are shown just to the right of the system figure. In the figures of the responses, A is the amplitude of response shown in red color and the dashed lines indicate its envelope. The responses represent only the qualitative trend and those are not drawn to any specific scale.
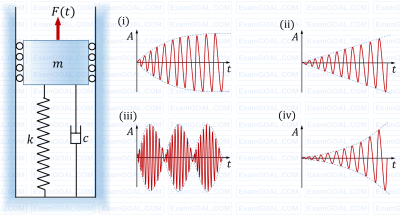
Four different parameter and forcing conditions are mentioned below.
(P) c > 0 and $ω=\sqrt{k/m}$
(Q) c < 0 and ω ≠ 0
(R) c = 0 and $\omega=\sqrt{k/m}$
(S) c = 0 and $\omega \cong\sqrt{k/m}$
Which one of the following options gives correct match (indicated by arrow →) of the parameter and forcing conditions to the responses?
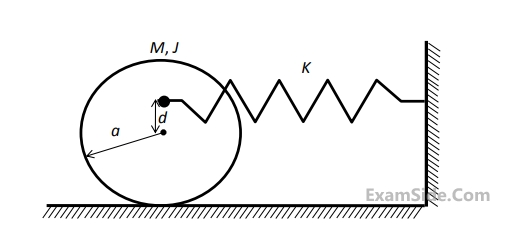
The natural frequency of this system in rad/s is given by
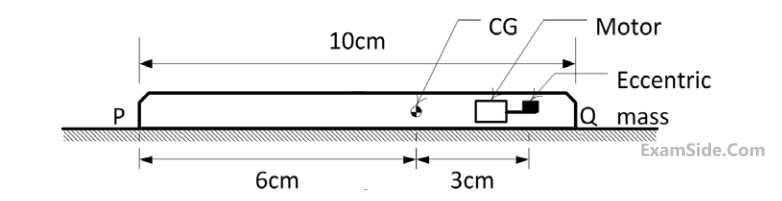
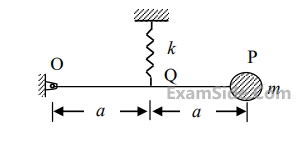
Given in addition that the eccentric mass = $$2$$ grams, eccentricity = $$2.19$$ mm, mass of the mobile = $$90$$ grams, g = $$9.81$$ $$m/{s^2}.$$ Uniform speed of the motor in $$RPM$$ for which the mobile will get just lifted off the ground at the end $$Q$$ is approximately

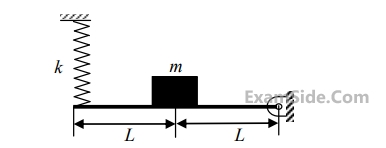
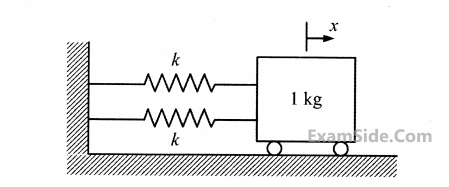

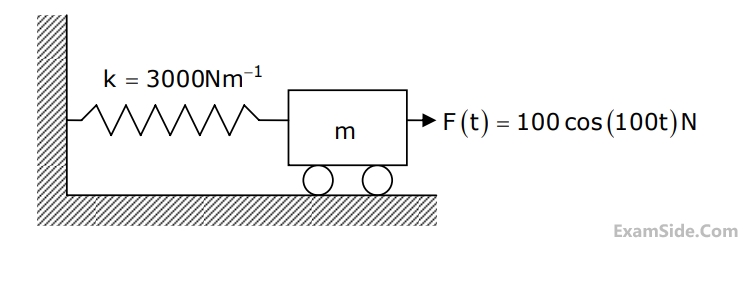

The amplitude of $$x(t)$$ after $$n$$ complete cycles is

The value of logarithmic decrement is
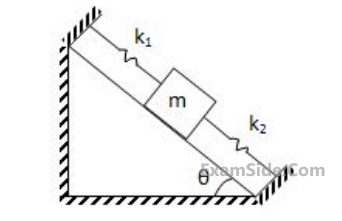
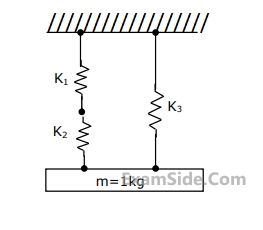
The value of critical damping of the system is:
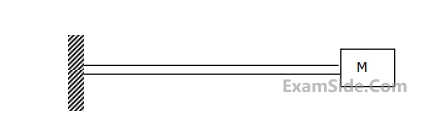
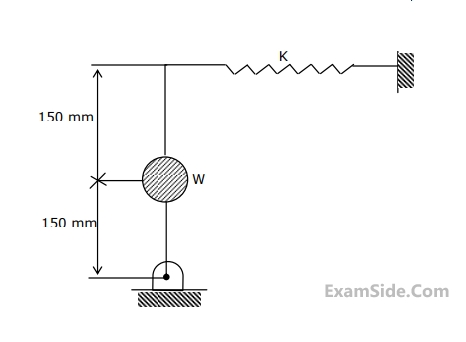
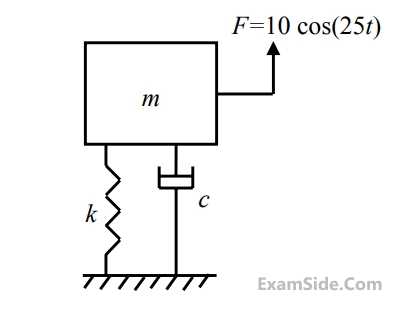
The damping coefficient in the vibration equation is given by

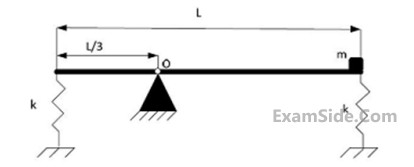
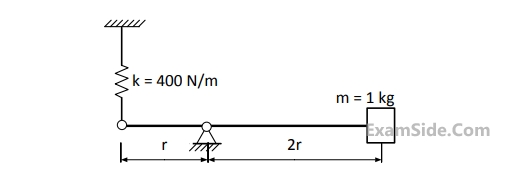
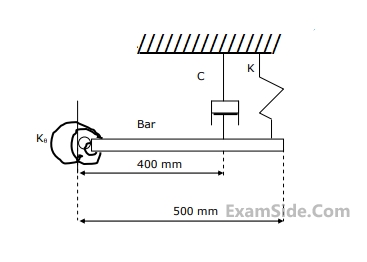
The un-damped natural frequency of oscillations of the bar about the hinge point is
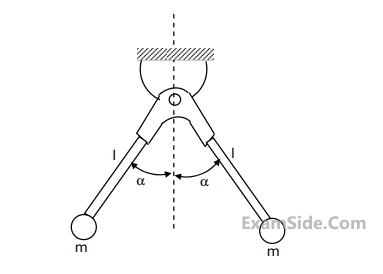
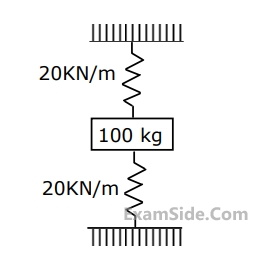
Marks 5