Convection · Heat Transfer · GATE ME

Marks 1

Consider incompressible laminar flow over a flat plate with freestream velocity of $u_{\infty}$. The Nusselt number corresponding to this flow velocity is $Nu_1$. If the freestream velocity is doubled, the Nusselt number changes to $Nu_2$. Choose the correct option for $Nu_{2}/Nu_{1}$.

GATE ME 2024

Consider a hydrodynamically fully developed laminar flow through a circular pipe with the flow along the axis (i.e., z direction). In the following statements, $T$ is the temperature of the fluid, $T_w$ is the wall temperature and $T_m$ is the bulk mean temperature of the fluid. Which one of the following statements is TRUE?

GATE ME 2024

Consider incompressible laminar flow of a constant property Newtonian fluid in an isothermal circular tube. The flow is steady with fully-developed temperature and velocity profiles. The Nusselt number for this flow depends on

GATE ME 2023

Which of the following non-dimensional terms is an estimate of Nusselt number?

GATE ME 2022 Set 2

Grashof number signifies the ratio of

GATE ME 2016 Set 3

The ratio of momentum diffusivity $$\left( \upsilon \right)$$ to thermal diffusivity $$\left( \alpha \right),$$ is called

GATE ME 2015 Set 3

In the laminar flow of air $$(Pr=0.7)$$ over a heated plate, if $$\delta $$ and $${\delta _T}$$ denote, respectively the hydrodynamic and thermal boundary layer thickness, then

GATE ME 2015 Set 2

For flow of viscous fluid over a flat plate, if the fluid temperature is the same as the plate temperature, the thermal boundary layer is

GATE ME 2015 Set 1

The Blasius equation related to boundary layer theory is a

GATE ME 2015 Set 1

Match Group $$A$$ with Group $$B$$

Group-A
$$P:$$$$\,\,\,\,\,\,\,$$ Biot number
$$Q:$$$$\,\,\,\,\,\,\,$$ Grashof number
$$R:$$$$\,\,\,\,\,\,\,$$ Prandtl number
$$S:$$$$\,\,\,\,\,\,\,$$ Reynolds number

Group-B
$$1:$$$$\,\,\,\,\,\,\,$$ Ratio of buoyancy to viscous force
$$2:$$$$\,\,\,\,\,\,\,$$ Ratio of inertia force to viscous force
$$3:$$$$\,\,\,\,\,\,\,$$ Ratio of momentum to thermal diffusivities
$$4:$$$$\,\,\,\,\,\,\,$$ Ratio of internal thermal resistance to boundary layer thermal resistance

GATE ME 2014 Set 4

For laminar forced convection over a flat plate, if the free stream velocity increases by a factor of $$2,$$ the average heat transfer coefficient

GATE ME 2014 Set 2

Consider a two-dimensional laminar flow over a long cylinder as shown in the figure below.

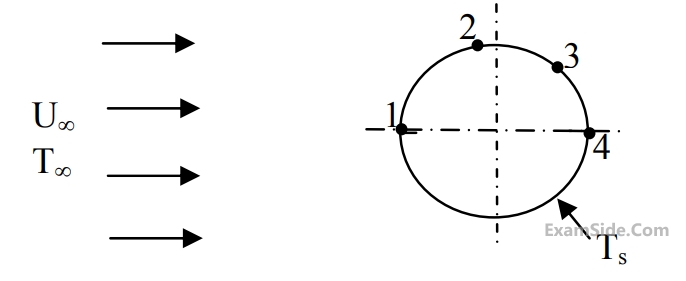
The free stream velocity is $${U_\infty }$$ and the free stream temperature $${T_\infty }$$ is lower than the cylinder surface temperature $${T_s}.$$ The local heat transfer coefficient is minimum at point

GATE ME 2014 Set 2

A coolant fluid at $${30^ \circ }C$$ flows over a heated flat plate maintained at a constant temperature of $${100^ \circ }C$$. The boundary layer temp distribution at a given location on the plate may be approximated as $$T=30+70exp(-y),$$ where $$y$$ (in $$m$$) is the distance normal to the plate and $$T$$ is in $$^ \circ C.$$ If thermal conductivity of the fluid is $$1.0W/mk,$$ the local convective heat transfer (in $$W/{m^2}K$$) at that location will be

GATE ME 2009

For flow of fluid over a heated plate, the following fluid properties are known: Viscosity $$=0.001Pa.s;$$ Specific heat at constant pressure $$=1$$ $$kJ/kgK;$$ Thermal conductivity $$=$$ $$W/mK,$$ The hydrodynamic boundary layer thickness at a specified location on the plate is $$1mm,$$ thermal boundary layer thickness at the same location is

GATE ME 2008

Heat transfer coefficients for free convection in gasses, forced convection in gases and vapors, and for boiling water lie, respectively, in the range of

GATE ME 1998

For air near atmospheric condition flowing over a flat plate the laminar thermal boundary layer is thicker than hydrodynamic boundary layer

GATE ME 1994

In pool boiling the highest $$HTC$$ occurs in

GATE ME 1990

For the fluid flowing over a flat plate with Prandtle number greater than unity, the thermal boundary layer for laminar forced convection

GATE ME 1988

Marks 2

A very large metal plate of thickness 𝑑 and thermal conductivity 𝑘 is cooled by a stream of air at temperature 𝑇∞ = 300 K with a heat transfer coefficient ℎ, as shown in the figure. The centerline temperature of the plate is TP. In which of the following case(s) can the lumped parameter model be used to study the heat transfer in the metal plate?

GATE ME 2023

Consider a hydrodynamically and thermally fully-developed, steady fluid flow of 1 kg/s in a uniformly heated pipe with diameter of 0.1 m and length of 40 m. A constant heat flux of magnitude 15000 W/m² is imposed on the outer surface of the pipe. The bulk-mean temperature of the fluid at the entrance to the pipe is 200 °C. The Reynolds number (Re) of the flow is 85000, and the Prandtl number (Pr) of the fluid is 5. The thermal conductivity and the specific heat of the fluid are 0.08 w.m¹K^-1 and 2600 J-kg¹K^-1, respectively. The correlation Nu = 0.023 Re^0.8 Pr^0.4 is applicable, where the Nusselt Number (Nu) is defined on the basis of the pipe diameter. The pipe surface temperature at the exit is _______ °C (round off to the nearest integer).

GATE ME 2022 Set 2

A fluid (Prandtl number, $$Pr=1$$) at $$500$$ $$K$$ flows over a flat plate of $$1.5$$ $$m$$ length, maintained at $$300$$ $$K.$$ The velocity of the fluid is $$10\,\,m/s.$$ Assuming kinematic viscosity, $$v = 30 \times {10^{ - 6}}\,\,{m^2}/s,$$ the thermal boundary layer thickness (in $$mm$$) at $$0.5$$ $$m$$ from the leading edge is _________.

GATE ME 2016 Set 1

For flow through a pipe of radius $$R,$$ the velocity and temperature distribution are as follows:
$$U\left( {r,x} \right) = {C_1}$$ and $$T\left( {r,x} \right) = {C_2}\left[ {1 - {{\left( {{r \over R}} \right)}^3}} \right],$$
where $${C_1}$$ and $${C_2}$$ are constants. The bulk mean temperature is given by

$${T_m} = {2 \over {{U_m}{R^2}}}\int\limits_0^R {u\left( {r,x} \right)T\left( {r,x} \right)rdr,} $$
with $${{U_m}}$$ being the mean velocity of flow. The value of $${T_m}$$ is

GATE ME 2015 Set 1

Water flows through a tube of diameter $$25mm$$ at an average velocity of $$1.0m/s.$$ The properties of water are $$\rho = 1000\,\,kg/{m^3},$$ $$\mu = 7.25 \times {10^{ - 4}}\,\,N.s/{m^2},$$ $$\,K = 0.625W/m.K,$$ $$Pr=4.85.$$ Using $$Nu=0.023$$ $$R{e^{0.8}}\,\,{\Pr ^{0.4}},$$ the convective heat transfer coefficient (in $$W/{m^2}.K$$) is ______________.

GATE ME 2014 Set 2

The non-dimensional fluid temperature profile near the surface of a convectively cooled flat plate is given by $${{{T_w} - T} \over {{T_w} - {T_\infty }}} = a + b{y \over L} + c{\left( {{y \over L}} \right)^2},$$ where $$y$$ is measured perpendicular to the plate, $$L$$ is the length, and $$a,b$$ and $$c$$ are arbitrary constants. $${{T_w}}$$ and $${{T_\infty }}$$ are wall and ambiyent temperatures, respectively. If the thermal conductivity of the fluid is $$k$$ and the wall heat flux is $$q'',$$ the Nusselt number $$\,{N_u} = {{q''} \over {{T_w} - {T_\infty }}}{L \over k}$$ is equal to

GATE ME 2014 Set 1

Consider one dimensional steady state heat conduction across a wall (as shown in figure below) of thickness $$30$$ $$mm$$ and thermal conductivity $$15$$ $$W/m.K.$$ At $$x=0,$$ a constant heat flux, $$q'' = 1 \times {10^5}\,\,W/{m^2}$$ is applied. On the other side of the wall, heat is removed from the wall by convection with a fluid at $${25^ \circ }C$$ and heat transfer coefficient of $$250W/{m^2}.K.$$ The temperature (in $${}^ \circ C$$), at $$x=0$$ is ___________

GATE ME 2014 Set 1

The ratios of the laminar hydrodynamic boundary layer thickness to thermal boundary layer thickness of flows of two fluids $$P$$ and $$Q$$ on a flat plate are $${1 \over 2}$$ and $$2$$ respectively. The Reynolds number based on the plate length for both the flows is $${10^4}.$$ The Prandtl and Nusselt numbers for $$P$$ are $${1 \over 8}$$ and $$35$$ respectively. The Prandtl and Nusselt number for $$Q$$ are respectively

GATE ME 2011

Match the following

List-$${\rm I}$$
$$P.$$ Compressible flow
$$Q.$$ Free surface flow
$$R.$$ Boundary layer flow
$$S.$$ Pipe flow
$$T.$$ Heat convection

List-$${\rm II}$$
$$U.$$ Renolds number
$$V.$$ Nussult number
$$W.$$ Weber number
$$X.$$ Froude number
$$Y.$$ Mach number
$$Z.$$ Skin friction coefficient

GATE ME 2010

The temp distribution within the Laminar thermal boundary layer over a heated isothermal flat plate is given by
$$\left( {T - {T_w}} \right)/\left( {{T_\infty } - {T_w}} \right) = \left( {3/2} \right)\,\,\left( {y/{\delta _t}} \right) - \left( {1/2} \right){\left( {y/{\delta _t}} \right)^3},$$
where $${{T_w}}$$ and $${{T_ \propto }}$$ are the temp of plate and free stream respectively, and $$'y'$$ is the normal distance measuread from the plate. The ratio of Average to the local Nussult number based on the thermal boundary layer thickness $${{\delta _t}}$$ is given by

GATE ME 2007

The average heat transfer coefficient on a thin hot vertical plate suspended in still air can be determined from observations of the change in plate temperature with time as it cools. Assume the plate temp to be uniform at any instant of time and radiation heat exchange with the surroundings is negligible. The ambient temperature is $${25^ \circ }C,$$ the plate has a total surface area of $$0.1{m^2}$$ and a mass of $$4$$ kg.

The specific heat of the plate material is $$2.5KJ/KgK.$$ The convective heat transfer coefficient in $$W/{m^2}K,$$ at instant when the plate temp is $${225^ \circ }C$$ and the change in plate temp with time $$dT/dt=-0.02K/s,$$ is

GATE ME 2007

An un-insulated air conditioning duct of rectangular cross section $$1\,\,m \times 0.5\,m,$$ carrying air at $${20^ \circ }C$$ with a velocity of $$10 m/s,$$ is exposed to an ambient of $${30^ \circ }C$$. Neglect the effect of duct construction material. For air in the range of $${20-30^ \circ }C,$$ data are as follows: thermal conductivity $$=0.025 W/m.K;$$ viscosity $$ = 18\mu Pa.s;$$ Prandtl number $$=0.73;$$ density $$= 1.2$$ $$kg/{m^3}.$$. The laminar flow Nusselt number is $$3.4$$ for constant wall temperature conditions and, for turbulent flow, $$Nu = 0.023\,\,R{e^{0.8}}\,{\Pr ^{0.33}}.$$

The Reynolds number for the flow is

GATE ME 2005

The heat transfer per meter length of the duct, in watts, is

GATE ME 2005

Consider a laminar boundary layer over a heated flat plate. The free stream velocity is $${U_\infty }.$$ At some distance $$x$$ from the leading edge the velocity boundary layer thickness is $${\delta _v}$$ and the thermal boundary layer is $${\delta _r}.$$ If the Prandtl number is greater than $$1,$$ then

GATE ME 2003

The properties of mercury at $$300K$$ are : density $$ = 13529kg/{m^3},$$ $${C_P} = 0.1393$$ $$kJ/kgK,$$ dynimic viscosity $$ = 0.1523\,\, \times \,\,{10^{ - 2}}\,\,N - s/{m^2}$$ and thermal conductivity $$=8.540$$ $$W/m$$-$$K$$. The Prandtl number of the mercury at $$300K$$ is

GATE ME 2002

Water (Prandtl number $$=6$$ ) flows over a flat plate which is heated over the entire length. Which one of the following relationship between the hydrodynamic boundary layer thickness $$\left( \delta \right)$$ and thermal boundary layer thickness $$\left( {{\delta _t}} \right)$$ is true

GATE ME 2001

Match List - $${\rm I}$$ with List - $${\rm II}$$ and select the correct answer using the code given below the Lists:

List - $${\rm I}$$
$$A.$$ Grashof number
$$B.$$ Schmid number
$$C.$$ Weber number
$$D.$$ Fourier number

List - $${\rm II}$$
$$1.$$ Mass diffusion
$$2.$$ Transient heat conduction
$$3.$$ Free convection
$$4.$$ Forced convection
$$5.$$ Surface tension
$$6.$$ Radiation

GATE ME 1996

A fluid flowing over a flat plate has the following properties: dynamic viscocity $$ = 25 \times {10^{ - 6}}\,\,kg/ms,$$ specific heat $$=2.0 $$ $$kJ/kgK,$$ thermal conductivity $$0.05W/mK.$$ The hydrodynamic boundary layer thickness is measured to be $$0.5$$ $$mm.$$ The thickness of the thermal boundary layer would be

GATE ME 1992