Linear Programming · Industrial Engineering · GATE ME

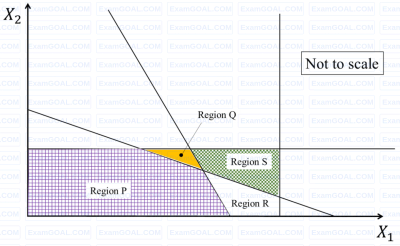
Which one of the options given represents the feasible region of the linear programming model:

𝑀𝑎𝑥𝑖𝑚𝑖𝑧𝑒 45𝑋₁ + 60𝑋₂

𝑋₁ ≤ 45

𝑋₂ ≤ 50

10𝑋₁ + 10𝑋₂ ≥ 600

25𝑋₁ + 5𝑋₂ ≤ 750

In a linear programming problem, if a resource is not fully utilized, the shadow price of that resource is

Simplex method of solving linear programming problem uses

If at the optimum in a linear programming problem, a dual variable corresponding to a particular primal constraint is zero, then it means that

At the current basic feasible solution (bfs) $v_0 (v_0 \in \mathbb{R}^5)$, the simplex method yields the following form of a linear programming problem in standard form:

minimize $z = -x_1 - 2x_2$

s.t.

$x_3 = 2 + 2x_1 - x_2$

$x_4 = 7 + x_1 - 2x_2$

$x_5 = 3 - x_1$

$x_1, x_2, x_3, x_4, x_5 \geq 0$

Here the objective function is written as a function of the non-basic variables. If the simplex method moves to the adjacent bfs $v_1 (v_1 \in \mathbb{R}^5)$ that best improves the objective function, which of the following represents the objective function at $v_1$, assuming that the objective function is written in the same manner as above?

A manufacturing unit produces two products Pl and P2. For each piece of P1 and P2, the table below provides quantities of materials M1, M2, and M3 required, and also the profit earned. The maximum quantity available per day for M1, M2 and M3 is also provided. The maximum possible profit per day is ₹ ______

	M1	M2	M3	Profit per piece ( ₹)
P1	2	2	0	150
P2	3	1	2	100
Maximum quantity available per day	70	50	40

Maximize $$\,\,\,\,\,\,\,\,\,Z = 5{x_1} + 3{x_2}$$
Subject to $$\,\,\,\,\,\,\,\,\,\,{x_1} + 2{x_2} \le 10,$$
$$\eqalign{ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1} - {x_2} \le 8, \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1},{x_2} \ge 0 \cr} $$

In the starting simplex tableau, $${x_1}$$ and $${x_2}$$ are non-basic variables and the value of $$Z$$ is zero. The value of $$Z$$ in the next simplex tableau is __________________.

Two models, $$P$$ and $$Q,$$ of a product earn profits of Rs. $$100$$ and Rs. $$80$$ per piece, respectively. Production times for $$P$$ and $$Q$$ are $$5$$ hours and $$3$$ hours, respectively, while the total production time available is $$150$$ hours. For a total batch size of $$40,$$ to maximize profit, the number of units of $$P$$ to be produced is ____________.

A firm uses a turning center, a milling center and a grinding machine to produce two parts. The table below provides the machining time required for each part and the maximum machining time available on each machine. The profit per unit on parts $${\rm I}$$ and $${\rm II}$$ are Rs. $$40$$ and Rs. $$100,$$ respectively. The maximum profit per week of the firm is Rs. _______________

Maximize $$\,\,\,\,Z = 15{x_1} + 20{x_2}$$
Subject to
$$\eqalign{ & 12{x_1} + 4{x_2} \ge 36 \cr & 12{x_1} - 6{x_2} \le 24 \cr & \,\,\,\,\,\,\,\,\,{x_1},\,\,{x_2} \ge 0 \cr} $$

The above linear programming problem has

For the linear programming problem:
$$\eqalign{ & Maximize\,\,\,\,\,Z = 3{x_1} + 2{x_2} \cr & Subject\,\,to\,\,\,\, - 2{x_1} + 3{x_2} \le 9 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1} - 5{x_2} \ge - 20 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1},\,\,{x_2} \ge 0 \cr} $$

The above problem has

Consider an objective function $$Z\left( {{x_1},{x_2}} \right) = 3{x_1} + 9{x_2}$$ and the constraints
$$\eqalign{ & {x_1} + {x_2} \le 8, \cr & {x_1} + 2{x_2} \le 4, \cr & {x_1} \ge 0,{x_2} \ge 0, \cr} $$

The maximum value of the objective function is ________________.

A linear programming problem is shown below.
$$\eqalign{ & Maximize\,\,\,\,3x + 7y \cr & Subject\,\,to\,\,\,3x + 7y \le 10 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4x + 6y \le 8 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x,\,\,y \ge 0 \cr} $$

It has ..............

One unit of product $${P_1}$$ requires $$3$$ $$kg$$ of resource $${R_1}$$ and $$1$$ $$kg$$ of resource $${R_2}$$. One unit of product $${P_2}$$ requires $$2$$ $$kg$$ of resource $${R_1}$$ and $$2$$ $$kg$$ of resource $${R_2}$$. The profits per unit by selling product $${P_1}$$ and $${P_2}$$ are Rs. $$2000$$ and Rs. $$3000$$ respectively. The manufacturer has $$90$$ $$kg$$ of resource $${R_1}$$ and $$100$$ $$kg$$ of resource $${R_2}$$.

The manufacturer can make a maximum profit of Rs.

One unit of product $${P_1}$$ requires $$3$$ $$kg$$ of resource $${R_1}$$ and $$1$$ $$kg$$ of resource $${R_2}$$. One unit of product $${P_2}$$ requires $$2$$ $$kg$$ of resource $${R_1}$$ and $$2$$ $$kg$$ of resource $${R_2}$$. The profits per unit by selling product $${P_1}$$ and $${P_2}$$ are Rs. $$2000$$ and Rs. $$3000$$ respectively. The manufacturer has $$90$$ $$kg$$ of resource $${R_1}$$ and $$100$$ $$kg$$ of resource $${R_2}$$.

The unit worth of resource $${R_2}$$. i.e. dual price of resource $${R_2}$$ in Rs. per $$kg$$ is

Consider the following Linear Programming problem $$(LLP)$$

Maximize: $$Z = 3{x_1} + 2{x_2}$$
$$\,\,$$ Subject $$\,\,$$ to
$$\eqalign{ & \,\,\,\,\,\,\,{x_1} \le 4 \cr & \,\,\,\,\,\,\,{x_2} \le 6 \cr & 3{x_1} + 2{x_2} \le 18 \cr & {x_1} \ge 0,\,\,{x_2} \ge 0 \cr} $$

Consider the Linear programme $$(LP)$$
Max $$4x$$ + $$6y$$
Subject to
$$\eqalign{ & \,\,\,\,\,\,\,\,\,\,\,3x + 2y \le 6 \cr & \,\,\,\,\,\,\,\,\,\,\,2x + 3y \le 6 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x,y \ge 0 \cr} $$

After introducing slack variables $$s$$ and $$t$$, the initial basic feasible solution is represented by the table below (basic variables are $$s=6$$ $$t=6,$$ and the objective function value is $$0$$).

After some simplex iterations, the following table is obtained

From this, one can conclude that

Consider the Linear programme $$(LP)$$
Max $$4x$$ + $$6y$$
Subject to
$$\eqalign{ & \,\,\,\,\,\,\,\,\,\,\,3x + 2y \le 6 \cr & \,\,\,\,\,\,\,\,\,\,\,2x + 3y \le 6 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x,y \ge 0 \cr} $$

The dual for the $$LP$$ is

Consider a linear programming problem with two variables and two constraints. The objective function is: Maximize $${x_1} + {x_2}.$$ The corner points of the feasible region are $$(0,0), (0,2), (2,0)$$ and $$(4/3, 4/3).$$

If an additional constraint $${x_1} + {x_2} \le 5$$ is added, the optimal solution is

Consider a linear programming problem with two variables and two constraints. The objective function is: Maximize $${x_1} + {x_2}.$$ The corner points of the feasible region are $$(0,0), (0,2), (2,0)$$ and $$(4/3, 4/3).$$

Let $${y_1}$$ and $${y_2}$$ be the decision variables of the dual and $${v_1}$$ and $${v_2}$$ be the slack variables of the dual of the given linear programming problem. The optimum dual variables are

A company produces two types of toys: $$P$$ and $$Q.$$ Production time of $$Q$$ is twice that of $$P$$ and the company has a maximum of $$2000$$ time units per day. The supply of raw material is just sufficient to produce $$1500$$ toys (of any type) per day. Toy type $$Q$$ requires an electric switch which is available @ $$600$$ pieces per day only. The company makes a profit of Rs.$$3$$ and Rs.$$5$$ on type $$P$$ and $$Q$$ respectively. For maximization of profits, the daily production quantities of $$P$$ and $$Q$$ toys should respectively be

A manufacturer produces two types of products, $$1$$ and $$2,$$ at production levels of $${x_1}$$ and $${x_2}$$ respectively. The profit is given is$$2{x_1} + 5{x_2}.$$ The production constraints are $$$\eqalign{ & {x_1} + 3{x_2} \le 40 \cr & 3{x_1} + {x_2} \le 24 \cr & {x_1} + {x_2} \le 10 \cr & {x_1} > 0,\,{x_2} > 0 \cr} $$$

The maximum profit which can meet the constraints is

A furniture manufacturer produces chairs and tables. The wood-working department is capable of producing $$200$$ chairs or $$100$$ tables or any proportionate combinations of these per week. The weekly demand for chairs and tables is limited to $$150$$ and $$80$$ units respectively. The profit from a chair is Rs.$$100$$ and that from a table is Rs.$$300.$$

$$(a)$$ Set up the problem as a Linear Program
$$(b)$$ Determine the optimum product mix for maximizing the profit.
$$(c)$$ What is the maximum profit?
$$(d)$$ If the profit of each table drops to Rs.200 per unit, what is the optimal mix and profit?

Solve the following linear programming problem by simplex method

$$\eqalign{ & Maximize\,\,\,\,\,\,4{x_1} + 6{x_2} + {x_3} \cr & Subject\,\,to\,\,\,\,\,\,2{x_1} - {x_2} + 3{x_3}\, \le 5 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1},{x_2},{x_3} \ge 0 \cr} $$

$$(a)$$$$\,\,\,\,\,\,\,$$ What is the solution to the above problem?

$$(b)$$$$\,\,\,\,\,\,\,$$ Add the constant $${x_2} \le 2$$ to the simplex table of part $$(a)$$ and find the solution.