Let a, b and $$\lambda $$ be positive real numbers. Suppose P is an end point of the latus return of the
parabola y² = 4$$\lambda $$x, and suppose the ellipse $${{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1$$ passes through the point P. If the tangents to the parabola and the ellipse at the point P are perpendicular to each other, then the eccentricity of the ellipse is

Let the circles

C₁ : x² + y² = 9 and C₂ : (x $$-$$ 3)² + (y $$-$$ 4)² = 16, intersect at the points X and Y. Suppose that another circle C₃ : (x $$-$$ h)² + (y $$-$$ k)² = r² satisfies the following conditions :

(i) Centre of C₃ is collinear with the centres of C₁ and C₂.

(ii) C₁ and C₂ both lie inside C₃ and

(iii) C₃ touches C₁ at M and C₂ at N.

Let the line through X and Y intersect C₃ at Z and W, and let a common tangent of C₁ and C₃ be a tangent to the parabola x² = 8$$\alpha $$y.

There are some expression given in the List-I whose values are given in List-II below.



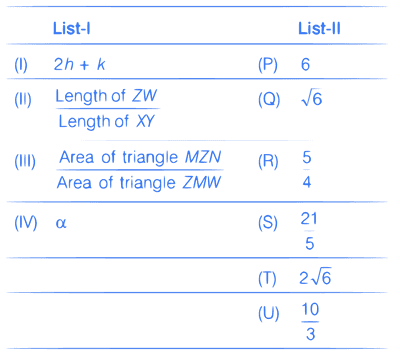
Which of the following is the only INCORRECT combination?

Let the circle C₁ : x² + y² = 9 and C₂ : (x $$-$$ 3)² + (y $$-$$ 4)² = 16, intersect at the points X and Y. Suppose that another circle C₃ : (x $$-$$ h)² + (y $$-$$ k)² = r² satisfies the following conditions :

(i) centre of C₃ is collinear with the centers of C₁ and C₂.

(ii) C₁ and C₂ both lie inside C₃, and

(iii) C₃ touches C₁ at M and C₂ at N.

Let the line through X and Y intersect C₃ at Z and W, and let a common tangent of C₁ and C₃ be a tangent to the parabola x² = 8$$\alpha $$y.

There are some expression given in the List-I whose values are given in List-II below.



Which of the following is the only CORRECT combination?

By appropriately matching the information given in the three columns of the following table.

Columns 1, 2 and 3 contain conics, equations of tangents to the conics and points of contact, respectively.

	Column - 1	Column - 2	Column - 3
(i)	$${x^2} + {y^2} = a$$	$$my = {m^2}x + a$$	$$\left( {{a \over {{m^2}}},\,{{2a} \over m}} \right)$$
(ii)	$${x^2}{a^2}{y^2} = {a^2}]$$	$$y = mx + a\sqrt {{m^2} + 1} $$	$$\left( {{{ - ma} \over {\sqrt {{m^2} + 1} }},\,{a \over {\sqrt {{m^2} + 1} }}} \right)$$
(iii)	$${y^2} = 4ax$$	$$y = mx + \sqrt {{a^2}{m^2} - 1} $$	$$\left( {{{ - {a^2}m} \over {\sqrt {{a^2}{m^2} + 1} }},\,{1 \over {\sqrt {{a^2}{m^2} + 1} }}} \right)$$
(iv)	$${x^2} - {a^2}{y^2} = {a^2}$$	$$y = mx + \sqrt {{a^2}{m^2} + 1} $$	$$\left( {{{ - {a^2}m} \over {\sqrt {{a^2}{m^2} - 1} }},\,{{ - 1} \over {\sqrt {{a^2}{m^2} - 1} }}} \right)$$

If a tangent to a suitable conic (Column 1) is found to be y = x + 8 and its point of contact is (8, 16), then which of the following options is the only CORRECT combination?